简要介绍

LPCNet 是一个 数字信号处理（DSP） 和 神经网络（NN）巧妙结合应用于语音合成中 vocoder 的工作，可以在普通的CPU上实时合成高质量语音。传统上，基于 DSP 的 vocoder 速度很快，但是合成的语音质量不是太好，而基于 NN 的 vocoder 语音质量更高，但通常复杂度太高，无法实时。
 

背景和动机

首先从语音产生机理的 source-filter 模型说起，这是上世纪70年代的东西，也是 LPC10、CELP、MELP 等 codec 的理论基础。这个模型把语音产生过程分解为类似信源、信道两个独立的模块。信源部分就是声带震动，发清音时没有震动就用白噪声建模，发浊音时喉咙有震动就用脉冲串建模；信道部分就是发不同音时口腔、鼻腔、舌头、嘴唇这些配合形成的通道，可以用一个全极点的 LPC 滤波器建模。这个模型非常简单，但是语音质量不太好。
然后是 WaveNet，它是 DeepMind 2016年提出的，不对语音做任何先验假设，而是用神经网络从数据中学习分布，它不直接预测语音样本值，而是通过一个采样过程来生成语音。它的语音质量非常好比之前所有基于参数的 vocoder 都要好，但是它生成语音太慢，大约需要几十 GFLOPS，主要原因是为了获得足够大的感受野卷积层做得太深太复杂。因此 DeepMind 和 Google Brain 提出 WaveRNN 用 RNN 建模提升效率，并且 RNN 的权重采用稀疏矩阵进一步降低运算量，尽管如此，WaveRNN 还是大约需要 10 GFLOPS, 这相比基于 DSP 的 codec 而言大约高两个数量级。  
最后来到 LPCNet, 作者 Jean-Marc Valin 也是 Opus Codec 的作者，是个编解码和信号处理的高手，他可能相信信号处理与神经网络结合才是更好的路，2017年就做了一个结合信号处理和神经网络做语音降噪的工作 RNNoise。
他觉得类比 source-filter 模型, 全神经网络的做法既要让 NN 建模 source 又要建模 filter 很难也很浪费，因为 filter 部分用 DSP 实现其实非常简洁高效，有经典的 Levinson-Durbin 算法，但是使用 NN 实现却可能非常复杂。因此他以 WaveRNN 为基础显式加入 LPC filter 模块来降低神经网络部分的复杂度。一个直觉的想法是 WaveRNN 需要为整个采样值建模，那么如果我将这个采样值分解成线性和非线性两部分，线性部分通过基于 DSP 的线性预测给出，神经网络仅需建模变化相对较小的非线性残余部分，这会是个更简单的任务，更少的神经元便可以胜任。 下面我们将详细分析 LPCNet 的细节。
 

网络分解

LPCNet 的主体网络结构如下图所示，这里忽略了 pcm 到 μ-law 的编码转换。因为特征提取以帧 (10ms, 160 样点）为单位进行，而语音生成是以样点为单位进行，因此 LPCNet 网络可以分解为两个子网络: Frame rate network 和 Sample rate network，外加一个计算 LPC 的模块。
网络的核心设计在 Sample rate network 部分，Frame rate network 主要为 Sample rate network 提供一个条件向量的输入，这个条件向量一帧计算一次，并在该帧时间内保持不变。LPC 计算模块则从输入特征中计算线性预测参数 LPC，LPC 也是一帧计算一次，并在帧内保持不变。
 

数据准备和训练

网络使用 CE 准则训练， 在 softmax 位置评估预测  分布和真实分布的交叉熵。测试时输入仅包含 features，训练时输入还包含  ，输出参考为  。这部分数据准备使用了原始语音  , 利用 features 计算出来的 LPC 产生线性预测  , 而  既是输入（延时）也是输出参考。 特别注意：尽管训练时有原始语音  , 这里  的计算仍然使用从特征中恢复的 LPC 而不是直接从  中估计的 LPC，这样处理能减少训练和测试的 mismatch。 训练和测试还有一个 mismatch: 因为训练时使用了原始语音，测试时仅有特征输入，通过零初始化的历史语音样值循环生成激励样值和语音样值，显然不一致，因此对输入语音做加噪处理以缓解 mismatch，噪声怎么加也比较重要，后文噪声注入部分介绍。另一个可以尝试的方法是 Scheduled Sampling。 此外为了增加训练数据的多样性（能量分布更多样），让原始语音反复经过一些随机的二阶 IIR 滤波器（零极点均在单位圆内的最小相位系统），这些滤波器的 gain 是随机的，滤波器的传输函数为：
其中  均服从  分布（这样零极点可严格在单位圆内）。 GRU 为 RNN 的一种变体，其方程如下：
 的输入  ，  的输入  ，注意到两个 GRU 都用到 f 的条件。 训练时将 pitch 处理成 64 维 embedding，然后接在原来的特征后，构成 102 维特征（原特征为 38维，实际上 18 到 36 维的 BFE 互相关系数直接置零了并没用，暂不确定这是代码遗留问题还是有意加上这些无意义的维度），因此第一个卷积层使用 128 个 filter, 第二个卷积层使用 102 个 filter, 以便和输入的 102 维一致； 作为网络输入的 μ-law 样值都首先处理成 128 维 embedding，输出分布直接与 μ-law 对应，8 bit 对应一个 256 维的分布，所以输出层大小为 256。 条件向量 f 也是 128 维；embedding 维度的选择不是很清楚，可能是作者试出来的。  

LPC 计算

语音采样率很高（比如 16 KHz), 相邻样本点有很强的相关性，通常假设语音采样值是一个自回归过程，也即当前时刻样本值可以近似由若干相邻历史时刻的样本值线性表示，误差可建模为高斯白噪声。可以参见前文的 source-filter 模型，二者正好是一个相反的过程，也即把残差信号当作激励源通过由 LPC 系数构成的全极点滤波器便可以恢复原始语音.
由历史数据和线性预测系数 LPC (  )，就可以迭代预测了，那么关键就在于如何计算  。这都是上世纪七八十年代的成熟理论，也可以不用细究。主要原理如下： 线性预测值为  ，根据相关性原理，最优线性预测参数时，残差  应当和  不相关。 因此，很容易得到一个线性方程，也叫normal equations. 矩阵求逆就可以得到最优解，不过矩阵求逆复杂为O(  )，注意到到  是Toeplitz矩阵，因此有快速算法也就是著名的Levinson-Durbin算法将复杂度降为O(  ). 可以看到，求解 LPC 主要需要求解自相关函数，若给定一帧语音数据，可以直接近似估计自相关函数。但是对于声码器，输入是一帧的特征，因此需要从特征中计算自相关函数。实际上从特征中计算 LPC 并不太准确，因为特征本身相比原始语音已经丢失了一些信息。但是从最终结果看并没有什么影响，这也正是神经网络的强大之处。  

特征

特征使用

论文中称使用 20 维特征，包括:

• 18 BFCC, Bark-Frequency Cepstral Coefficients
• 2 pitch parameter (pitch, correlation)

BFCC 和 语音识别常用的 MFCC 类似，都是利用人类听觉特性，尽管 Bark scale 是根据人耳对响度感知实验确定的刻度，而 Mel scale 是根据人耳对音高感知实验确定的刻度，二者最终分的频带很类似，都是低频分辨率高，高频分辨率低，和线性频率对应关系都近似对数关系，因此我觉得这个工作中 BFCC 替换成 MFCC 特征应该也可以。该工作并没有严格使用 Bark Frequency, 而是使用了和 Opus 编码器一样的频带转换，作者称 Bark Frequency 低频带宽太窄，会导致样本太少参数估计不准。下图中共用了 22 个频带，最高频到 20KHz, 对于 16KHz 采样的语音，最高频只需到 8KHz 即可，因此去掉高频段的 4 个频带，剩下 18 个频带。   代码中准备了 55 维特征，包括:

• 18 BFCC
• 18 Bark-Frequency Energy (BFE) 互相关系数，为 x[n] 和 x[n−T] ( T 为 pitch) 对应BFE的互相关系数，这部分特征并没有真正使用，代码中直接置零，可能是之前代码遗留的冗余
• pitch
• gain (和 correlation function 有关，for removing doubling pitch)
• log(e) (e 为 LPC residual)
• 16 LPC ( LPC 从 BFCC 计算获得，首先 BFCC 通过 IDCT 然后 EXP 恢复成 BFE, 然后通过线性插值得到线性频谱（功率谱），然后 IFFT 得到自相关函数，最后通过 Levinson Durbin 算法计算 LPC )

网络测试时使用了前 38 维特征，因为最后的 17 维和 LPC 有关的特征可以通过 BFCC 计算得到；网络训练时则使用了全部 55 维特征，以便更快训练。不过无论训练还是测试，代码中并没有真正使用 18 个 BFE 互相关系数，因此真正使用的特征正如论文所述 20 维。

特征提取

单独考虑声码器，特征从原始语音中提取。

• BFCC 通过如下过程获得（和 MFCC 提取非常一致，二者仅在频带划分有差异)
  • 波形数据通过 FFT 到频谱
  • 频谱按 Bark 频率分成 18 个频带，计算每个频带内的能量（通过三角窗加权，也可以理解为三角滤波获取频谱包络）
  • Log 压缩动态范围得到倒谱
  • DCT 去相关得到最终的 BFCC
• pitch 参数通过一个基于互相关函数的 open-loop search 获得

整体考虑一个合成系统时，特征从前端模型中预测获得，前端模型以文本为输入，输出预测的语音特征。这里又有个 mismatch, 前文提到单纯声码器部分的训练和测试的 mismatch 采用了噪声注入以缓解。 这里的 mismatch 可能用前端模型预测的语音特征（而不是真实语音提取的特征）来训练声码器会更好，细节我不清楚，论文中也未涉及完整语音合成系统的前端模型和声码器对接的问题。
 

DualFC 输出层

作者称使用 DualFC 层相比 FC 层在同等参数下最终生成语音效果会略好些，他的直觉是确定一个数值在 μ-law 的某个量化区间里需要两次比较，而每个 FC 可实现一次比较。可视化权重也发现这个直觉 make sense。
DualFC 的输出通过 softmax 激活函数产生概率分布，然后从这个分布中采样激励信号（或线性预测残差), 激励信号加上线性预测信号就得到最终的输出信号。
返回大纲

采样过程

直接采样会引入太多噪声，引入一个常数 c 来控制采样过程，总体思路是给浊音的采样更多确定性，当当前帧为浊音有 pitch 时，给概率大的候选更大的权重，相当于冷却和降低随机性。  为 pitch correlation， T = 0.002 砍掉概率太小的候选。
 

量化和预加重

量化编码方面本文和WaveNet都使用了 8-bit μ-law，而 WaveRNN 使用 16-bit pcm。pcm 是线性线性编码均匀量化，优点是解码简单，缺点是压缩到 8-bit 时量化噪声很大，因此通常都用 16-bit。常见的 wav 格式文件就是采用 pcm16 量化编码。 8-bit μ-law 考虑了语音样值的统计分布，发现语音样值其实主要集中在 0 附近幅值较小的地方，且幅值越大概率越小，这很好理解，比如常见的高斯分布和拉普拉斯分布都有这样的特点。因此，一方面考虑语音的统计分布后，给幅值小的地方更多比特更小的量化误差，幅值大的地方更少比特更大的量化误差可以整体最优；另一方面，人类对于噪声的感知可能主要是对信噪比敏感，因此让量化噪声正比于信号幅度也很合理，这正好可以推导出对数特性的压缩曲线。8-bit μ-law 只有 256 个可能值，因此作为神经网络的输出层更为简单。 非均匀量化本质上是先通过一个非线性函数映射到另一空间，然后在映射的空间中做均匀量化，下图是两种常见的非均匀量化 μ-law 和 A-law 的映射函数。 下图是 μ-law 量化编码时具体采用的折线近似，这里仅考虑大于零的情况，另一半以原点中心对称可得。( 注：下图中分成 8 段用 3 bit, 然后每段再细分为 16 段用 4 bit, 符号 1 bit, 共 8 bit)  本文还采用了预加重滤波来提升高频能量，传输函数为  ， 相当于  ，是个高通滤波器。采用预加重的理由是语音信号能量通常集中在低频段，那么分频带考虑信噪比时就会出现高频段信噪比太小，量化噪声在高频处过于显著，因此事先提升一下高频能量，最后合成完语音后再用  压一压高频能量, 这可以显著降低合成语音的感知噪声。
 

噪声注入

为了缓解声码器训练和测试的 mismatch，训练时往输入语音里注入噪声，作者发现如果仅仅往输入语音里加噪，而使用干净的参考激励训练，生成语音会不太自然；输入语音加噪后，线性预测和激励都基于加噪的语音重新计算，使得网络输入和参考激励都同步引入噪声效果更好。作者也发现在 μ-law 域加噪更好。如下图所示。
更新：作者更新了代码，目前的噪声注入方式有些改变，直接对  的 μ-law 进行加噪。如下图所示：
 

矩阵稀疏化

这部分主要是 WaveRNN 的工作， 其作者发现 RNN 里同等参数量时权重用大而稀疏的矩阵会比小而稠密的矩阵好，因此初期正常训练一定 iter 后，就开始每隔一定 iter 让 weight 乘以一个二值 mask 强制稀疏化，并且训练越往后非零权重数量越少。权重稀疏化原则上根据稀疏度设置硬阈值砍掉小权重，不过考虑到计算和存储效率，稀疏化以 16x1 或 4x4 的分块为单位（要么去掉整个分块要么保留整个分块）。本文作者做的改动是一直保留对角位置的权重。稀疏化的主要目的是降低测试时计算复杂度（增加了训练复杂度），因此本工作中仅对  的 3 个和循环相关的矩阵  做稀疏化（因为  比较小可不做)。
 

Embedding 以及计算简化

这部分主要是为了加速合成语音，是在测试阶段，权重都训练好固定了。那么计算最大开销就在 sample rate 的 GRU 环节。作者的思路是对非循环部分都预先计算好。显然 μ-law 的输入  都只有 256 种可能，因此作者先将 μ-law Embedding 转成 128 维，然后把 256 个可能 embeding 和 GRU 中相关 非循环 矩阵相乘结果存储，这样合成时就可以通过查找表完成该部分计算。同时条件向量 f 也是一帧仅需计算一次，因此在帧内也可以把 f 和 GRU 里对应矩阵相乘结果存储复用。
 

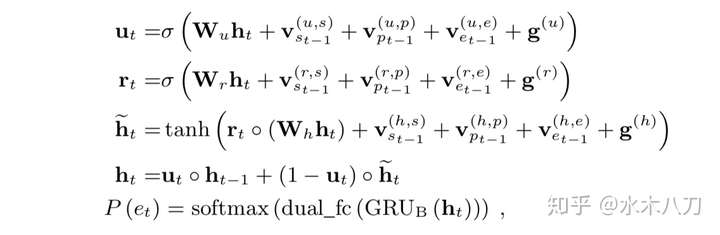
性能评估

计算复杂度

显然合成语音时的计算量主要在 Sample Rate Network 里的两个 GRU 部分（因为 Frame Rate Network 一帧才计算一次）。假设一个 weight 涉及 2 次运算(乘法和加法各一次），因此 LPCNet Inference 复杂度约为：  分别为  神经元数，  为稀疏矩阵的density （也即非零值）比例，仅  采用稀疏矩阵，  比较小采用稠密矩阵。非循环部分已经预先计算好了，因此仅考虑循环部分计算量。Q为输出层大小，Fs为采样率。 实验中取  , 其余计算量预估再加 0.5 GFLOPS， 这样整个声码器计算量约为2.8 GFLOPS。FFTNet (声称比原始 WaveNet 计算复杂度低）约 16 GFLOPS, WaveRNN 约 10 GFLOPS, SampleRNN 约 50 GFLOPS。  

合成语音质量

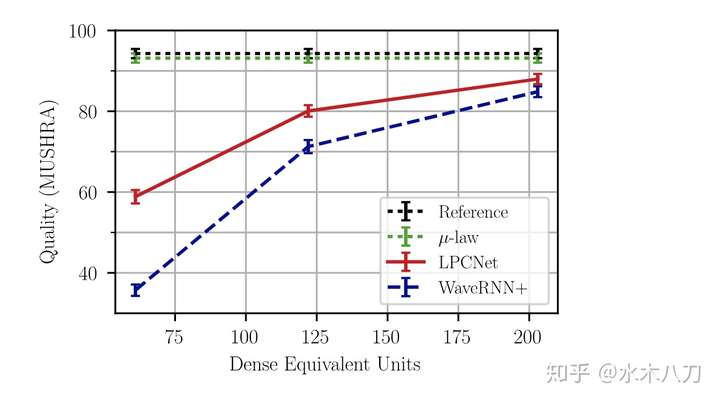
作者提到 LPCNet 可以应用于 speaker-dependent 和 speaker-independent 场景，作者挑战了更难的 speaker-independent 语音合成。这里 speaker-independent 具体含义我不太清楚。 不过根据本人实验，单说话人效果非常好；男女混合多说话人训练的模型倾向于平均模型，合成的语音有些含糊不清。另外一个有趣的实验现象是用一个女生的语音训练了单说话人模型，用另外一个女生的数据测试也能合成非常自然的语音，不确定是否是偶然现象。
作者的实验中训练语料使用了 4 小时 NTT Multi-Lingual Speech Database for Telephonometry，评价准则采用 MUSHRA-like listening test。 MUSHRA-like Listening Test: 两男两女说的 8 句话，分别让 100 个人听然后打分，分数越高说明语音质量越好，满分为 100。黑线为原始 PCM16 的 Reference, 绿线为 μ-law 的 Reference，可见 μ-law 压缩后语音质量几乎没有下降。 
红线和蓝线分别是 LPCNet 和 WaveRNN 的合成语音，横轴是  的等价神经元数  ，越大模型越复杂。对比测试了三个不同大小的网络，分别对应  的神经元数  =192, 384, 640, 对应等价神经元数为  = 61, 122, 203, 同时 WaveRNN 测试了同等复杂度的网络。可见同等复杂度下 LPCNet 比 WaveRNN 合成语音质量更高。
 

总结

本文展示了通过结合传统线性预测技术显著提高神经网络声码器合成效率的尝试。此外，本文的其他贡献还包括：信号 embedding, 改进的采样机制，μμ-law 量化前预加重滤波。作者认为这个模型可以应用到 Text-to-Speech、Speech Compression（低比特率编码）、Time Stretching（变速不变调）、Packet Loss Concealment（丢包补偿）等领域。因为本文使用的线性预测模块还没有包含长时预测部分（ 线性预测  除了包含  还加入  等 )，作者下一步也会探索把长时预测部分结合进来进一步减小网络复杂度。

个人感想

• 从这篇工作来看，DSP + NN 的门槛非常高，首先必须对 DSP 非常熟才可能有相关 insight, 其次更重要的是要有非常强的工程能力处理好各种细节将结合的优势真正凸显（可能还要加上坚定的信念去优化细节），普通人还是老老实实调调参做端到端吧。
• 其实 DSP + NN 在语音识别中倒是并不陌生，MFCC 就是 DSP 部分，简单稳定优雅，似乎也一直很难被端到端神经网络超越。本文给我的启示是：鲁棒语音识别中的 MFCC 模块从能效比角度考虑是否必须保留？ 也即如果某个前端模型相比传统 MFCC 性能有优势，是否可以通过把该前端增加的复杂度转移到后端声学模型中让 MFCC 前端继续保持优势？ 那么鲁棒语音识别前端的优化该何去何从？
• 有些场景只看性能无需考虑效率，因此复杂的 WaveNet 或复杂的语音识别前端仍然有其价值。

 

参考文献

1. https://zhuanlan.zhihu.com/p/54952637
2. https://blog.csdn.net/qingkongyeyue/article/details/52149839
3. https://blog.csdn.net/kaixinshier/article/details/72142889

LPCNet Demo
LPCNet paper
WaveRNN paper
Source Filter Model