DBSCAN clustering - Wikipedia

Density-based spatial clustering of applications with noise (DBSCAN) is a data clustering algorithm proposed by Martin Ester, Hans-Peter Kriegel, Jörg Sander and Xiaowei Xu in 1996. [1] It is a density-based clustering algorithm: given a set of points in some space, it groups together points that are closely packed together (points with many nearby neighbors), marking as outliers points that lie alone in low-density regions (whose nearest neighbors are too far away). substantial [səb'stænʃ(ə)l]：adj. 大量的，实质的，内容充实的 n. 本质，重要材料 In 2014, the algorithm was awarded the test of time award (an award given to algorithms which have received substantial attention in theory and practice) at the leading data mining conference, KDD. ACM SIGKDD Conference on Knowledge Discovery and Data Mining，KDD Association for Computing Machinery's (ACM) Special Interest Group (SIG) on Knowledge Discovery and Data Mining，SIGKDD

History

In 1972, Robert F. Ling published “The Theory and Construction of $k$-Clusters” [2] in The Computer Journal with a closely related, with an estimated runtime complexity of O($n^3$). [2] In 1996, DBSCAN has a worst-case of O($n^2$), and the database-oriented range-query formulation of DBSCAN allows for index acceleration. The algorithms differ in their handling of border points. worst-case ['wə:stkeis]：adj. 作最坏打算的，最糟情况的 query ['kwɪərɪ]：n. 疑问，质问，疑问号，查询 vt. 询问，对…表示疑问，vi. 询问，表示怀疑 border ['bɔːdə]：n. 边境，边界，国界 vt. 接近，与…接壤；在…上镶边 vi. 接界，近似

Preliminary

Consider a set of points in some space to be clustered. Let $epsilon$ be a parameter specifying the radius of a neighborhood with respect to some point. For the purpose of DBSCAN clustering, the points are classified as core points, (density-) reachable points and outliers, as follows:
为了进行 DBSCAN 聚类，所有的点被分为核心点，(密度) 可达点及局外点，详请如下：

• A point $p$ is a core point if at least $minPts$ points are within distance $epsilon$ of it (including $p$).
  如果一个点 $p$ 在距离 $epsilon$ 范围内有至少 minPts 个点 (包括自己)，则这个点被称为核心点。
• A point $q$ is directly reachable from $p$ if point $q$ is within distance $epsilon$ from core point $p$. Points are only said to be directly reachable from core points.
• A point $q$ is reachable from $p$ if there is a path $p_{1}$, …, $p_{n}$ with $p_{1} = p$ and $p_{n} = q$, where each $p_{i+1}$ is directly reachable from $p_{i}$. Note that this implies that all points on the path must be core points, with the possible exception of $q$.
• All points not reachable from any other point are outliers or noise points.
  所有不由任何点可达的点都被称为 outliers or noise points。

Now if $p$ is a core point, then it forms a cluster together with all points (core or non-core) that are reachable from it. Each cluster contains at least one core point; non-core points can be part of a cluster, but they form its “edge”, since they cannot be used to reach more points.
如果 $p$ 是核心点，则它与所有由它可达的点 (包括核心点和非核心点) 形成一个聚类，每个聚类拥有最少一个核心点，非核心点也可以是聚类的一部分，但它是在聚类的边缘位置，因为它不能达至更多的点。 preliminary [prɪ'lɪmɪn(ə)rɪ]：n. 准备，预赛，初步措施 adj. 初步的，开始的，预备的 radius ['reɪdɪəs]：n. 半径，半径范围，桡骨，辐射光线，有效航程 outlier ['aʊtlaɪə]：n. 异常值，露宿者，局外人，离开本体的部分
In this diagram, minPts = 4. Point A and the other red points are core points, because the area surrounding these points in an $epsilon$ radius contain at least 4 points (including the point itself). Because they are all reachable from one another, they form a single cluster. Points B and C are not core points, but are reachable from A (via other core points) and thus belong to the cluster as well. Point N is a noise point that is neither a core point nor directly-reachable.
在这幅图里，minPts = 4，点 A 和其他红 {MOD}点是核心点，因为它们的 $epsilon$-邻域 (图中红 {MOD}圆圈) 里包含最少 4 个点 (包括自己)，由于它们之间相互相可达，它们形成了一个聚类。点 B 和点 C 不是核心点，但它们可由 A 经其他核心点可达，所以也属于同一个聚类。点 N 是局外点，它既不是核心点，又不由其他点可达。 one another：彼此，互相 Reachability is not a symmetric relation since, by definition, no point may be reachable from a non-core point, regardless of distance (so a non-core point may be reachable, but nothing can be reached from it). Therefore, a further notion of connectedness is needed to formally define the extent of the clusters found by DBSCAN. Two points $p$ and $q$ are density-connected if there is a point $o$ such that both $p$ and $q$ are reachable from $o$. Density-connectedness is symmetric.
可达性 (Reachability) 不是一个对称关系，因为根据定义，没有点是由非核心点可达的，但非核心点可以是由其他点可达的。所以为了正式地界定 DBSCAN 找出的聚类，进一步定义两点之间的连结性 (Connectedness)：如果存在一个点 $o$ 使得点 $p$ 和点 $q$ 都是由 $o$ 可达的，则点 $p$ 和点 $q$ 被称为 (密度) 连结的，而连结性是一个对称关系。 A cluster then satisfies two properties:

• All points within the cluster are mutually density-connected.
• If a point is density-reachable from any point of the cluster, it is part of the cluster as well.

定义了连结性之后，每个聚类都符合两个性质：

• 一个聚类里的每两个点都是互相连结的；
• 如果一个点 $p$ 是由一个在聚类里的点 $q$ 可达的，那么 $p$ 也在 $q$ 所属的聚类里。

mutually [ˈmjuːtʃuəli]：adv. 互相地，互助 reachable ['riːtʃəbl]：adj. 可获得的，可达成的 symmetric [sɪ'metrɪk]：adj. 对称的，匀称的 notion ['nəʊʃ(ə)n]：n. 概念，见解，打算 connectedness [kə'nektidnis]：n. 连通性

Algorithm

Original Query-based Algorithm

DBSCAN requires two parameters: $epsilon$ (eps) and the minimum number of points required to form a dense region (minPts). It starts with an arbitrary starting point that has not been visited. This point’s $epsilon$-neighborhood is retrieved, and if it contains sufficiently many points, a cluster is started. Otherwise, the point is labeled as noise. Note that this point might later be found in a sufficiently sized $epsilon$-environment of a different point and hence be made part of a cluster.
DBSCAN 需要两个参数：$epsilon$ (eps) 和形成高密度区域所需要的最少点数 (minPts)，它由一个任意未被访问的点开始，然后探索这个点的 $epsilon$-邻域，如果 $epsilon$-邻域里有足够的点，则建立一个新的聚类，否则这个点被标签为 noise。注意这个点之后可能被发现在其它点的 $epsilon$-邻域里，而该 $epsilon$-邻域可能有足够的点，届时这个点会被加入该聚类中。 sufficiently [sə'fɪʃəntlɪ]：adv. 充分地，足够地 If a point is found to be a dense part of a cluster, its $epsilon$-neighborhood is also part of that cluster. Hence, all points that are found within the $epsilon$-neighborhood are added, as is their own $epsilon$-neighborhood when they are also dense. This process continues until the density-connected cluster is completely found. Then, a new unvisited point is retrieved and processed, leading to the discovery of a further cluster or noise.
如果一个点位于一个聚类的密集区域里，它的 $epsilon$-邻域里的点也属于该聚类，当这些新的点被加进聚类后，如果它 (们) 也在密集区域里，它 (们) 的 $epsilon$-邻域里的点也会被加进聚类里。这个过程将一直重复，直至不能再加进更多的点为止，这样，一个密度连结的聚类被完整地找出来。然后，一个未曾被访问的点将被探索，从而发现一个新的聚类或 noise。 retrieve [rɪ'triːv]：vt. 检索，恢复，重新得到 vi. 找回猎物 n. 检索，恢复，取回 DBSCAN can be used with any distance function [1][3] (as well as similarity functions or other predicates).[4] The distance function (dist) can therefore be seen as an additional parameter. predicate [ˈprɛdɪˌkeɪt]：vt. 断定为…，使…基于 vi. 断言，断定 n. 谓语，述语 adj. 谓语的，述语的 The algorithm can be expressed in pseudocode as follows: [3] DBSCAN(DB, distFunc, eps, minPts) { C = 0 /* Cluster counter */ for each point P in database DB { if label(P) ≠ undefined then continue /* Previously processed in inner loop */ Neighbors N = RangeQuery(DB, distFunc, P, eps) /* Find neighbors */ if |N| < minPts then { /* Density check */ label(P) = Noise /* Label as Noise */ continue } C = C + 1 /* next cluster label */ label(P) = C /* Label initial point */ Seed set S = N {P} /* Neighbors to expand */ for each point Q in S { /* Process every seed point */ if label(Q) = Noise then label(Q) = C /* Change Noise to border point */ if label(Q) ≠ undefined then continue /* Previously processed */ label(Q) = C /* Label neighbor */ Neighbors N = RangeQuery(DB, distFunc, Q, eps) /* Find neighbors */ if |N| ≥ minPts then { /* Density check */ S = S ∪ N /* Add new neighbors to seed set */ } } } } where RangeQuery can be implemented using a database index for better performance, or using a slow linear scan: RangeQuery(DB, distFunc, Q, eps) { Neighbors = empty list for each point P in database DB { /* Scan all points in the database */ if distFunc(Q, P) ≤ eps then { /* Compute distance and check epsilon */ Neighbors = Neighbors ∪ {P} /* Add to result */ } } return Neighbors } DBSCAN 算法使用以下伪代码表述，当中变量根据原文刊登时的命名： DBSCAN(D, eps, MinPts) { C = 0 for each point P in dataset D { if P is visited continue next point mark P as visited NeighborPts = regionQuery(P, eps) if sizeof(NeighborPts) < MinPts mark P as NOISE else { C = next cluster expandCluster(P, NeighborPts, C, eps, MinPts) } } } expandCluster(P, NeighborPts, C, eps, MinPts) { add P to cluster C for each point P' in NeighborPts { if P' is not visited { mark P' as visited NeighborPts' = regionQuery(P', eps) if sizeof(NeighborPts') >= MinPts NeighborPts = NeighborPts joined with NeighborPts' } if P' is not yet member of any cluster add P' to cluster C } } regionQuery(P, eps) return all points within P's eps-neighborhood (including P) 这个算法可以按照如下方式简化：
(1) “has been visited” 和 “belongs to cluster C” 可结合起来。
(2) “expandCluster” 程序不必抽出来，因为它只在一个位置被调用。
以上算法没有以简化方式呈现，以反映原本出版的版本。此外，regionQuery 是否包含 P 并不重要，它等价于改变 MinPts 的值。

Abstract Algorithm

The DBSCAN algorithm can be abstracted into the following steps: [3]

1. Find the points in the $epsilon$ (eps) neighborhood of every point, and identify the core points with more than minPts neighbors.
2. Find the connected components of core points on the neighbor graph, ignoring all non-core points.
3. Assign each non-core point to a nearby cluster if the cluster is an $epsilon$ (eps) neighbor, otherwise assign it to noise.

A naive implementation of this requires storing the neighborhoods in step 1, thus requiring substantial memory. The original DBSCAN algorithm does not require this by performing these steps for one point at a time. component [kəm'pəʊnənt]：adj. 组成的，构成的n. 成分，组件，元件 naive [naɪ'iːv; nɑː'iːv]：adj. 天真的，幼稚的 substantial [səb'stænʃ(ə)l]：adj. 大量的，实质的，内容充实的 n. 本质，重要材料

Complexity

DBSCAN visits each point of the database, possibly multiple times (e.g., as candidates to different clusters). For practical considerations, however, the time complexity is mostly governed by the number of regionQuery invocations. DBSCAN executes exactly one such query for each point, and if an indexing structure is used that executes a neighborhood query in O(log n), an overall average runtime complexity of O(n log n) is obtained (if parameter ε is chosen in a meaningful way, i.e. such that on average only O(log n) points are returned). Without the use of an accelerating index structure, or on degenerated data (e.g. all points within a distance less than $epsilon$), the worst case run time complexity remains O($n^{2}$). The distance matrix of size $(n^{2}-n)/2$ can be materialized to avoid distance recomputations, but this needs O($n^{2}$) memory, whereas a non-matrix based implementation of DBSCAN only needs O(n) memory.
DBSCAN 对数据库里的每一点进行访问，可能多于一次 (例如作为不同聚类的候选者)，但在现实的考虑中，时间复杂度主要受 regionQuery 的调用次数影响，DBSCAN 对每点都进行刚好一次调用，且如果使用了特别的编号结构，则总平均时间复杂度为 O(n log n) ，最差时间复杂度则为 O($n^{2}$)。可以使用 O($n^{2}$) 空间复杂度的距离矩阵以避免重复计算距离，但若不使用距离矩阵，DBSCAN 的空间复杂度为 O(n)。 invocation [,ɪnvə(ʊ)'keɪʃ(ə)n]：n. 祈祷，符咒，(法院对另案的) 文件调取，(法权的) 行使 govern ['gʌv(ə)n]：vt. 管理，支配，统治，控制 vi. 居支配地位，进行统治 materialize [mə'tɪrɪəlaɪz]：vt. 使具体化，使有形，使突然出现，使重物质而轻精神 vi. 实现，成形，突然出现 recomputation ['ri:kəmpju:'teiʃən]：n. 重新计算，重新估计 degenerate [dɪ'dʒen(ə)rət]：vt. 使退化，恶化 vi. 退化，堕落 adj. 退化的，堕落的 n. 堕落的人

Advantages

(1) DBSCAN does not require one to specify the number of clusters in the data a priori, as opposed to $k$-means.
(2) DBSCAN can find arbitrarily shaped clusters. It can even find a cluster completely surrounded by (but not connected to) a different cluster. Due to the MinPts parameter, the so-called single-link effect (different clusters being connected by a thin line of points) is reduced.
(3) DBSCAN has a notion of noise, and is robust to outliers.
(4) DBSCAN requires just two parameters and is mostly insensitive to the ordering of the points in the database. (However, points sitting on the edge of two different clusters might swap cluster membership if the ordering of the points is changed, and the cluster assignment is unique only up to isomorphism.)
(5) DBSCAN is designed for use with databases that can accelerate region queries, e.g. using an R* tree.
(6) The parameters minPts and $epsilon$ can be set by a domain expert, if the data is well understood.
(1) 相比 $k$-means，DBSCAN 不需要预先声明聚类数量。
(2) DBSCAN 可以找出任何形状的聚类，甚至能找出一个聚类，它包围但不连接另一个聚类，另外，由于 MinPts 参数，single-link effect (不同聚类以一点或极幼的线相连而被当成一个聚类) 能有效地被避免。
(3) DBSCAN 能分辨噪音 (局外点)。
(4) DBSCAN 只需两个参数，且对数据库内的点的次序几乎不敏感 (两个聚类之间边缘的点有机会受次序的影响被分到不同的聚类，另外聚类的次序会受点的次序的影响)。
(5) DBSCAN 被设计成能配合可加速范围访问的数据库结构，例如 R* 树。
(6) 如果对数据有足够的了解，可以选择适当的参数以获得最佳的分类。 priori [praɪ'ɔ:raɪ]：adj. 先验的，优先的 (等于 a priori) adv. 先验地 (等于 a priori) specify ['spesɪfaɪ]：vt. 指定，详细说明，列举，把…列入说明书 as opposed to：与…截然相反，对照 domain expert：n. 领域专家 insensitive [ɪn'sensɪtɪv]：adj. 感觉迟钝的，对…没有感觉的 isomorphism [,aɪsəʊ'mɔːfɪzəm]：n. 类质同像，类质同晶，同形 expectation-maximization，EM：最大期望
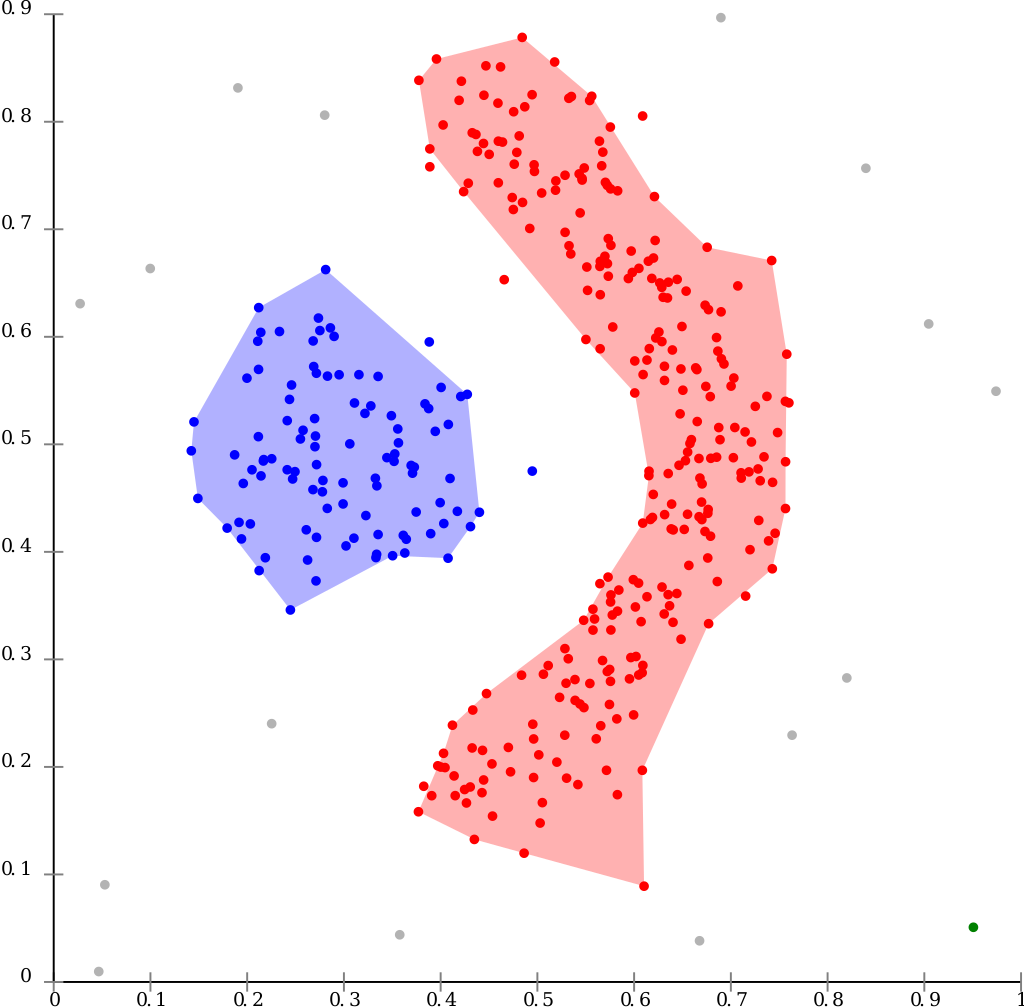
DBSCAN can find non-linearly separable clusters. This dataset cannot be adequately clustered with k-means or Gaussian Mixture EM clustering.

Disadvantages

(1) DBSCAN is not entirely deterministic: border points that are reachable from more than one cluster can be part of either cluster, depending on the order the data are processed. For most data sets and domains, this situation does not arise often and has little impact on the clustering result: [3] both on core points and noise points, DBSCAN is deterministic. DBSCAN* [6] is a variation that treats border points as noise, and this way achieves a fully deterministic result as well as a more consistent statistical interpretation of density-connected components.
(2) The quality of DBSCAN depends on the distance measure used in the function regionQuery(P, $epsilon$). The most common distance metric used is Euclidean distance. Especially for high-dimensional data, this metric can be rendered almost useless due to the so-called “Curse of dimensionality”, making it difficult to find an appropriate value for $epsilon$. This effect, however, is also present in any other algorithm based on Euclidean distance.
(3) DBSCAN cannot cluster data sets well with large differences in densities, since the minPts-$epsilon$ combination cannot then be chosen appropriately for all clusters. [5]
(4) If the data and scale are not well understood, choosing a meaningful distance threshold $epsilon$ can be difficult.
(1) DBSCAN 不是完全决定性的：在两个聚类交界边缘的点会视乎它在数据库的次序决定加入哪个聚类，幸运地，这种情况并不常见，而且对整体的聚类结果影响不大。DBSCAN 对 core points and noise points 都是决定性的。DBSCAN* 是一种变化了的算法，把边界点视为噪音，达到完全决定性的结果。
(2) DBSCAN 聚类分析的质量受函数 regionQuery(P, $epsilon$) 里所使用的度量影响，最常用的度量是欧几里得距离，尤其在高维度数据中，由于受所谓维数灾难影响，很难找出一个合适的 $epsilon$，但事实上所有使用欧几里得距离的算法都受维数灾难影响。
(3) 如果数据库里的点有不同的密度，而该差异很大，DBSCAN 将不能提供一个好的聚类结果，因为不能选择一个适用于所有聚类的 minPts-$epsilon$ 参数组合。
(4) 如果没有对资料和比例的足够理解，将很难选择适合的 $epsilon$ 参数。 meaningful ['miːnɪŋfʊl; -f(ə)l]：adj. 有意义的，意味深长的 render ['rendə]：vt. 致使，提出，实施，着 {MOD}，以…回报 vi. 给予补偿 n. 打底，交纳，粉刷 curse [kɜːs]：n. 诅咒，咒骂 vt. 诅咒，咒骂 vi. 诅咒，咒骂 deterministic [dɪ,tɜːmɪ'nɪstɪk]：adj. 确定性的，命运注定论的 entirely [ɪn'taɪəlɪ; en-]：adv. 完全地，彻底地 arise [ə'raɪz]：vi. 出现，上升，起立 consistent [kən'sɪst(ə)nt]：adj. 始终如一的，一致的，坚持的 interpretation [ɪntɜːprɪ'teɪʃ(ə)n]：n. 解释，翻译，演出 See the section below on extensions for algorithmic modifications to handle these issues.

Parameter estimation

Every data mining task has the problem of parameters. Every parameter influences the algorithm in specific ways. For DBSCAN, the parameters $epsilon$ and minPts are needed. The parameters must be specified by the user. Ideally, the value of $epsilon$ is given by the problem to solve (e.g. a physical distance), and minPts is then the desired minimum cluster size. ideally [aɪ'dɪəl(l)ɪ; aɪ'diːəl(l)ɪ]：adv. 理想地，观念上地 MinPts: As a rule of thumb, a minimum minPts can be derived from the number of dimensions D in the data set, as minPts ≥ D + 1. The low value of minPts = 1 does not make sense, as then every point on its own will already be a cluster. With minPts ≤ 2, the result will be the same as of hierarchical clustering with the single link metric, with the dendrogram cut at height $epsilon$. Therefore, minPts must be chosen at least 3. However, larger values are usually better for data sets with noise and will yield more significant clusters. As a rule of thumb, minPts = 2 * dim can be used, [4] but it may be necessary to choose larger values for very large data, for noisy data or for data that contains many duplicates. [3] rule of thumb：拇指规则，大拇指规则，经验法则 derive [dɪ'raɪv]：vt. 源于，得自，获得 vi. 起源 make sense：有意义，讲得通，言之有理 hierarchical [haɪə'rɑːkɪk(ə)l]：adj. 分层的，等级体系的 dendrogram ['dendrəgræm]：n. 系统树图 $epsilon$: The value for $epsilon$ can then be chosen by using a $k$-distance graph, plotting the distance to the $k$