http://www.songho.ca/dsp/convolution/convolution2d_separable.html
By the definition of Convolution 2D; 
Since convolution is commutative (x[n] * y[n] = y[n] * x[n]), swap the order of convolution; 
And, if h[m, n] is separable to (M×1) and (1×N); 
Therefore, substitute h[m, n] into the equation; 
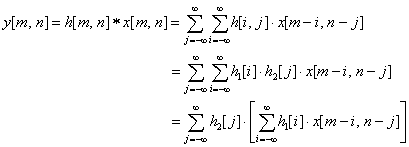Since the definition of convolution 1D is; 
 
it is convolving with input and h1, then convolve once again with the result of previous convolution and h2. Therefore, the separable 2D convolution is performing twice of 1D convolution in horizontal and vertical direction. 
And, convolution is associative, it does not matter which direction perform first. Therefore, you can convolve withh2[n] first then convolve with h1[m] later.

Example

Compute y[1,1] by using separable convolution method and compare the result with the output of normal convolution 2D.  
Input  
Separable Kernel i) Using convolution 2D 
ii) Using Separable Convolution 2D 
First, do the vertical convolution 1D where the row is n=1, and the column is m=0,1,2; 
 

Then, do the horizontal convolution with above result where column is m=1;