对于初学数字信号（Digital Signal Processing，DSP）的人来说，这几种变换是最为头疼的，它们是数字信号处理的理论基础，贯穿整个信号的处理。 FS：时域上任意连续的周期信号可以分解为无限多个正弦信号之和，在频域上就表示为离散非周期的信号，即时域连续周期对应频域离散非周期的特点，这就是傅立叶级数展开（Fourier Series，FS），它用于分析连续周期信号。 FT：是傅立叶变换（Fourier Transform，FT），它主要用于分析连续非周期信号，由于信号是非周期的，它必包含了各种频率的信号，所以具有时域连续非周期对应频域连续非周期的特点。

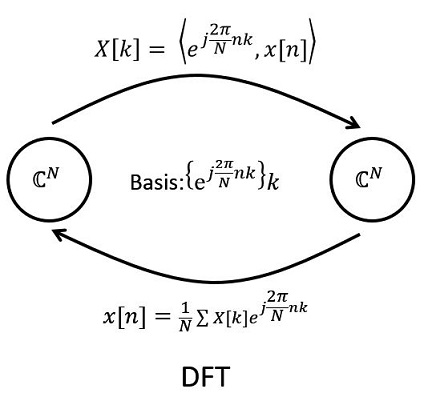
FS和FT 都是用于连续信号频谱的分析工具，它们都以傅立叶级数理论问基础推导出的。时域上连续的信号在频域上都有非周期的特点，但对于周期信号和非周期信号又有在频域离散和连续之分。 在自然界中除了存在温度，压力等在时间上连续的信号，还存在一些离散信号，离散信号可经过连续信号采样获得，也有本身就是离散的。例如，某地区的年降水量或平均增长率等信号，这类信号的时间变量为年，不在整数时间点的信号是没有意义的。用于离散信号频谱分析的工具包括DFS，DTFT和DFT。 DTFT：是离散时间傅立叶变换（Discrete-time Fourier Transform，DTFT） ，它用于离散非周期序列分析，根据连续傅立叶变换要求连续信号在时间上必须可积这一充分必要条件，那么对于离散时间傅立叶变换，用于它之上的离散序列也必须满足在时间轴上级数求和收敛的条件；由于信号是非周期序列，它必包含了各种频率的信号，所以DTFT对离散非周期信号变换后的频谱为连续的，即有时域离散非周期对应频域连续周期的特点。

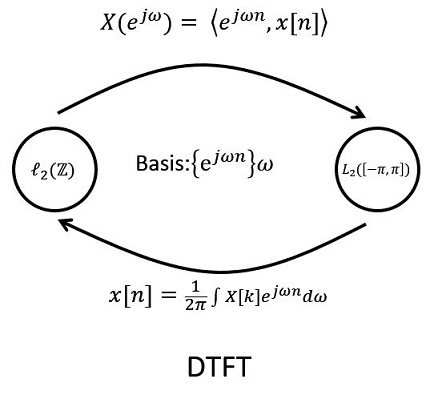
当离散的信号为周期序列时，严格的讲，傅立叶变换是不存在的，因为它不满足信号序列绝对级数之和收敛（绝对可和）这一傅立叶变换的充要条件，但是采用离散傅立叶级数（Discrete Fourier Series ，DFS）这一分析工具仍然可以对其进行傅立叶分析。 我们知道周期离散信号是由无穷多相同的周期序列在时间轴上组成的，假设周期为N，即每个周期序列都有N个元素，而这样的周期序列有无穷多个，由于无穷多个周期序列都相同，所以可以只取其中一个周期就足以表示整个序列了，这个被抽出来表示整个序列特性的周期称为主值周期，这个序列称为主值序列。然后以N对应的频率作为基频构成傅立叶级数展开所需要的复指数序列ek(n)=e−j2πnk/N，用主值序列与复指数序列（代表各个频率的基序列）取相关（乘加运算），得出每 个主值在各频率上的频谱分量，这样就表示出了周期序列的频谱特性。 根据DTFT，对于有限长序列作Z变换（Z-transformation）或离散傅立叶变换都是可行的，或者说有限长序列的频域和复频域分析在理论上都已经解决；但对于数字系统，无论是Z变换还是离散傅立叶变换的适用方面都存在一些问题，重要是因为频率变量的连续性性质（DTFT变换出连续频谱），不便于数字运算和储存。 参考DFS，可以采用类似DFS的分析方法对解决以上问题。可以把有限长非周期序列假设为一无限长周期序列的一个主直周期，即对有限长非周期序列进行周期延拓，延拓后的序列完全可以采用DFS进行处理，即采用复指数基频序列和此有限长时间序列取相关，得出每个主值在各频率上的频谱分量以表示出这个“主值周期”的频谱信息。 由于DFT借用了DFS，这样就假设了序列的周期无限性，但在处理时又对区间作出限定（主值区间），以符合有限长的特点，这就使DFT带有了周期性。另 外，DFT只是对一周期内的有限个离散频率的表示，所以它在频率上是离散的，就相当于DTFT变换成连续频谱后再对其采样，此时采样频率等于序列延拓后的周期N，即主值序列的个数。 引入一篇博客中的图组，来进一步说明：


补充两条性质：

1 在一个域的相乘等于另一个域的卷积 2 与脉冲函数的卷积，在每个脉冲的位置上将产生一个波形的镜像

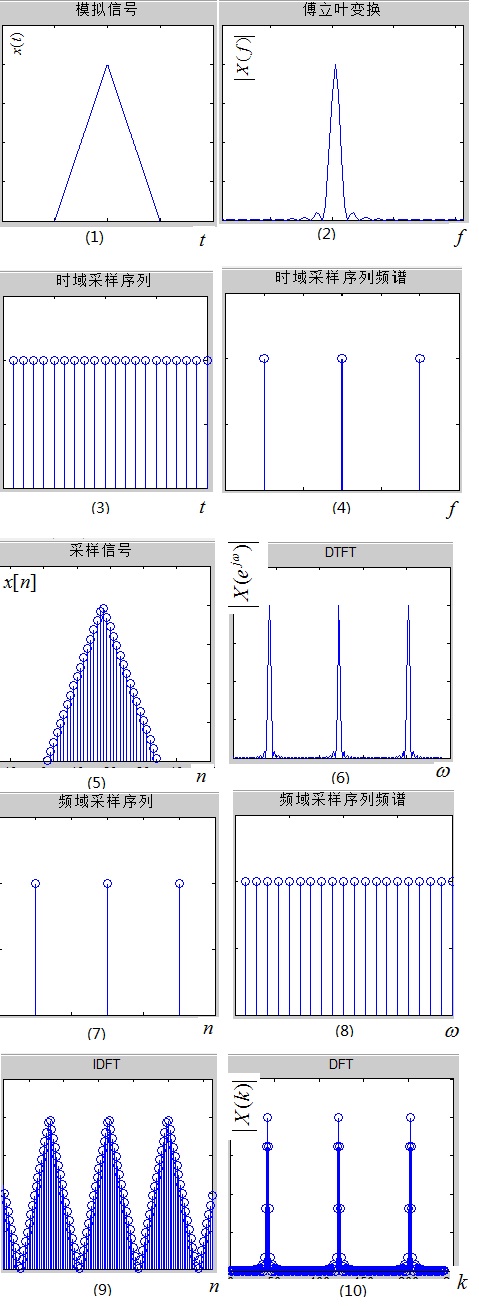
首先来说图(1)和图(2)，对于一个模拟信号，如图(1)所示，要分析它的频率成分，必须变换到频域，这是通过傅立叶变换（FT）得到的，于是有了模拟信号的频谱，如图(2)。（PS：此时时域和频域都是连续的！） 计算机只能处理数字信号，需要将原模拟信号在时域离散化，即在时域对其进行采样，采样脉冲序列如图(3)所示，该采样序列的频谱如图(4)，可见它的频谱也是一系列的脉冲。所谓时域采样，就是在时域对信号进行相乘，(1)×(3)后可以得到离散时间信号x[n]，如图(5)所示。由性质1知，时域的相乘相当于频域的卷积，那么，图(2)与图(4)进行卷积，由于性质2，在每个脉冲的位置上将产生一个波形的镜像，于是得到图(6)，它就是图(5)所示离散时间信号x[n]的DTFT。（PS：此时时域是离散的，而频域依然是连续的。) 经过上面两个步骤，我们得到的信号依然不能被计算机处理，因为频域既连续，又周期。我们自然就想到，既然时域可以采样，为什么频域不能采样呢？这样不就时域与频域都离散化了吗？没错，接下来对频域在进行采样，频域采样信号的频谱如图(8)所示，它的时域波形如图(7)。现在我们进行频域采样，即频域相乘，图(6)×图(8)得到图(10)，由性质1，频域相乘相当于时域卷积，图(5)和图(7)卷积得到图(9)，不出所料的，镜像会呈周期性出现在各个脉冲点处。我们取图(10)周期序列的主值区间，并记为X(k)，它就是序列x[n]的DFT。可见，DFT只是为了计算机处理方便，在频率域对DTFT进行的采样并截取主值而已。有人可能疑惑，对图(10)进行IDFT（逆离散傅里叶变换），回到时域即图(9)，它与原离散信号图(5)所示的x[n]不同呀，它是x[n]的周期性延拓！没错，因此你去查找一个IDFT的定义式，是不是对n的取值区间进行限制了呢？这一限制的含义就是，取该周期延拓序列的主值区间，即可还原x[n]！ FFT呢？FFT的提出完全是为了快速计算DFT而已，它的本质就是DFT！我们常用的信号处理软件MATLAB或者DSP软件包中，包含的算法都是FFT而非DFT。 DFS，是针对时域周期信号提出的，如果对图(9)所示周期延拓信号进行DFS，就会得到图(10)，只要截取其主值区间，则与DFT是完全的一一对应的精确关系。这点对照DFS和DFT的定义式也可以轻易的看出。因此DFS与DFT的本质是一样的，只不过描述的方法不同而已。 结束语：

• 如此折腾，为伊消得人憔悴，不过是为了打破现实模拟世界与计算机数字世界的界限。

参考资料：

• http://www.cnblogs.com/BitArt/archive/2012/11/24/2786390.html