作者：BerenCamlost

参考资料：

1. 老师PPT：百度 {MOD}链接 提取码: dhn4
2. 数字信号处理课本
3. 超星视频：B站视频链接

第三章 DFT

3.1 各种傅里叶变换

傅里叶变换前（时域） 傅里叶变换后（频域） 非周期连续 非周期连续 周期连续 非周期离散 非周期离散 周期连续 周期离散 周期离散 一个域的离散对应另外一个域的周期
一个域的连续对应另外一个域的非周期

3.2 DFS——离散傅里叶级数

3.2.1 一个重要的算子

$W_N=e^{-j(2pi /N)}$

3.2.2 计算公式

$ilde{X}[K]= sum_{n=0}^{N-1} ilde{x}[n]e^{-j(2pi/N)kn}= sum_{n=0}^{N-1} ilde{x}[n]W_N^{kn}$

3.3 DFT——（有限长序列的）离散傅里叶变换

3.3.1 主值序列和周期延拓

$x[n]=left{egin{matrix} ilde{x}[n] & 0leqslant nleqslant N-1\ 0 & others end{matrix} ight.$
$x[n]= ilde{x}[n]R_N[n]$

3.3.2 计算公式

$X[K]=DFT[x[n]]=sum_{n=0}^{N-1}x[n]W_N^{kn},0leqslant kleqslant N-1$
$x[n]=IDFT[X[k]]=sum_{n=0}^{N-1}X[k]W_N^{-kn},0leqslant kleqslant N-1$

• 将这个公式和上面的DFS公式相对比，可以发现DFT是DFS的主值序列

3.3.3 DFT和DTFT的关系

• N点离散傅里叶变换X[k]是以$2pi /N$为采样间隔，对该序列的离散时间傅里叶变换$X(e^{jomega })$在一个周期内$(0leqslant omega < 2pi )$的等频率间隔采样。
• 对于Z变换，就是单位圆上等间隔取样。

3.3.4 频域采样

• 频域采样定理：如果序列x[n]长度为M，若对其$X(e^{jomega })$在$(0leqslant omega < 2pi )$进行等间隔采样，采样间隔为$Delta omega =2pi /N$，采样点频率为 $omega _k=2pi k/N$，得到N点的Y[k]，仅当采样点数N>=M
  时，才能由Y[k]恢复x[n]，即x[n]=IDFT [Y[k] ]，否则将产
  生时域的混叠失真，不能由Y[k]无失真的恢复原序列

3.4 DFT性质

3.4.1 线性

3.4.2 循环移位

1. 周期延拖，周期为N
2. 时移
3. 取主值区间

具体图示如下图所示：

• 循环移位也称为圆周移位，原因可以由下图解释：
  
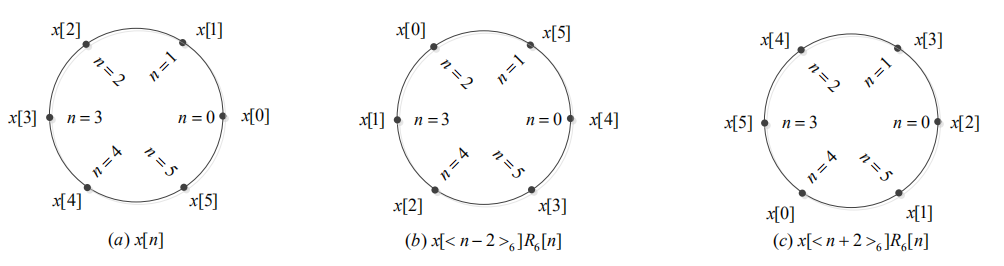
• 循环移位定理：
  $DFT[x[<n-m>_N]R_N[n]]=W_N^{km}X[k]$

3.4.3 圆周共轭对称

1. 圆周偶对称：x[n]=x[N-n]
2. 圆周奇对称：x[n]=-x[N-n]

圆周偶对称性 圆周奇对称性 X[k]的实部 X[k]的虚部 $egin{vmatrix}X[k]end{vmatrix}$ arg[X[k]]

3.4.4 循环卷积

$y[n]=sum_{m=0}^{N-1}x_1[m]x_2[<n-m>_N],0leqslant nleqslant N-1$
记作:

• 循环卷积定理：
  
• 循环卷积和线性卷积的关系：两个有限长序列的N点循环卷积yc[n]，是这两个有限长序列的线性卷积y1[n]以N为周期进行周期延拓后的主值序列。

循环卷积的一种简单算法

在我们计算循环卷积的时候，通常是先移位再相乘，然后求和。这种简单算法的思路是，先相乘，再移位，最后求和。这种方法类似于计算线性卷积时的列表法，或者是竖式法。这里用一个例子来说明：

【例】：设x1[N]={1,2,3,4}, x2[N]={2,1,3}, 求4点循环卷积
【答】：
先对x2[N]补1个零，然后列式：
1，2，3，4；；前两行是源数据
2，1，3，0
2，4，6，8；；先使2和{1，2，3，4}相乘
4，1，2，3；；然后让1和{1，2，3，4}相乘，但是起始位置和第二行的1对齐，并且将最后的4移动到最前面
9，12，3，6；；然后让3和{1，2，3，4}相乘，但是起始位置和第二行的3对齐，并且将最后的9，12移动到最前面
0，0，0，0
；；纵向求和，结果为
15，17，11，17

3.4.5 帕斯瓦尔定理

• x[N]和y[N]的N点DFT分别为X[k]、Y[k]，则有
  $sum_{n=0}^{N-1}x[n]y^*[n]=frac{1}{N}sum_{n=0}^{N-1}X[k]Y^*[k]$
• 当x[n]=y[n]时，有
  $sum_{n=0}^{N-1}egin{vmatrix} x[n] end{vmatrix}^2=frac{1}{N}sum_{n=0}^{N-1}egin{vmatrix} X[k] end{vmatrix}^2$