class="markdown_views prism-dracula">

1.基本概念

有向图：图间的连线有方向
完全图：每个对应定点之间相互连接。

2.图的存储

　2.1 邻接矩阵

　　用一个n阶方阵R来存放图中各结点的关联信息。有连线用1表示，否则用0表示。

上面的有向图和无向图对应的邻接矩阵如下：（无向图的邻接矩阵一定关于主对角线对称）

　2.2 邻接表

　　把每个顶点的邻接顶点用链表示出来，然后用一个一位数组来顺序存储上面每个链表的头指针。
上面的有向图对应的邻接表如下：

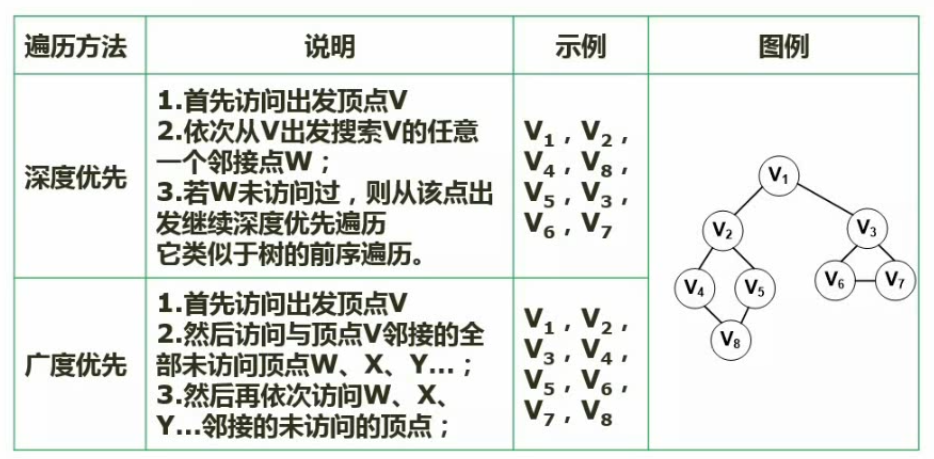
3.图的遍历

4.图的时间复杂度计算

查找所有顶点的邻接顶点的时间复杂度（n个顶点e条边）
（与深度优先和广度优先无关，只与存储方式有关）
邻接矩阵存储时：O（n^2）
邻接表存储时：O（n+e）

5.图的拓扑排序

我们把用有向边表示活动之间开始的先后关系，这种有向图称为用顶点表示活动网络，简称AOV网络。

上图的拓扑序列有：02143567 ， 01243657 ， 02143657 ， 01243567

6.图的最小生成树

图当中很多的线去掉，只留下若干条线，把所以结点连贯起来，留下来的线都是权值较小的，从而使得留下来的线的权值加起来是最小的。

数和图最大的区别在于数无法形成环路。树的节点数为n，其线的条数最多为n-1，否则就构成了图。
普里姆算法：从一个结点出发，比如A，将A定义为红点集，其他集为蓝点集，找出红点集到蓝点集里最短的距离。
①A-B 100 ， A-C 400 ， A-F 250 ， A-E 200，选择A-B，将B纳入红点集
②A-C 400 ， A-F 250 ， A-E 200 ， B-C 400 ， B-F 300 ， 选择A-E，将E纳入红点集
③A-C 400 ， A-F 250 ， B-C 400 ， B-F 300 ， E-F 400 ，选择A-F，将F纳入红点集
④A-C 400 ， B-C 400 ， F-C 400 ， F-D 200，选择F-D，将D纳入红点集
⑤A-C 400 ， B-C 400 ， F-C 400 ， D-C 300，选择D-C、
注意：过程中不能形成环路，选出的5条线即为最小生成树
克鲁斯卡尔算法：在不形成环路的前提下，依次选择最短距离的n-1连线
A-B ，A-E ， F-D ， A-F ， B-F（×） ， C-D ，