一、实验原理

1.时域离散信号的概念

在时间轴的离散点上取值的信号，称为离散时间信号。通常，离散时间信号用x(n)表示，其幅度可以在某一范围内连续取值。 由于信号处理所使用的设备和装置主要是计算机或专用的信号处理芯片，均以有限的位数来表示信号的幅度，因此，信号的幅度也必须“量化”，即取离散值。我们把时间和幅度上均取离散值的信号称为时域离散信号或数字信号。 在MATLAB语言中，时域的离散信号可以通过编写程序直接生成，也可以通过对连续信号等间隔抽样获得。 另外，抽样得到的离散信号只有在一定的抽样条件下，才能反映原连续时间信号的基本特征。

2.用MATLAB生成离散信号须注意的问题

1)有关数组与下标

MATLAB中处理的数组，将下标放在变量后面的小扩号内，且约定从1开始递增。
例如x＝［5，4，3，2，1，0］，表示x(1)＝5，x(2)＝4，x(3)＝3，x(4)＝2，x(5)＝1，x(6)＝0。 要表示一个下标不由1开始的数组x(n)，一般应采用两个矢量，如： n＝［－3：5］；
x＝［1，－1，3，2，0，－2，－1，2，1］； 这表示了一个含9个采样点的矢量。n为一组时间矢量，对应x有：x(－3)＝1，x(－2)＝－1，x(－1)＝3，…，x(5)＝1。 代码： n=-3:5; x=[1,-1,3,2,0,-2,-1,2,1]; stem(n,x,'filled') xlabel('时间n') ylabel('幅度x(n)') 输出：

2)信号的图形绘制

从本质上讲，MATLAB及其任何计算机语言处理的信号都是离散信号。当我们把信号的样点值取得足够密，作图时采用特殊的指令，就可以把信号处理成连续信号。 在MATLAB中，离散信号与连续信号有时在程序编写上是一致的，只是在作图时选用不同的绘图函数。 连续信号作图使用plot函数，绘制线性图；离散信号作图则使用stem函数，绘制脉冲杆图。

3.常用的时域离散信号及其程序

常用的时域离散信号主要有单位抽样序列、单位阶跃序列、实指数序列、复指数序列、正(余)弦序列、锯齿波序列、矩形波序列以及随机序列等典型信号。 有些信号的生成方法不止一种，下面对常用的时域离散信号进行介绍。

1)单位抽样序列

单位抽样序列的表示式为： 实例1： 代码： %用MATLAB的关系运算式来产生单位抽样序列 ：范围从-5到5 n0=0;%于n0处产生冲激 n1=-5;n2=5; n=n1:n2; x= n==n0;%生成离散信号x(n) stem(n,x,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([n1,n2,0,1.1*max(x)]) %确定横坐标和纵坐标的取值范围 title('单位脉冲序列'); xlabel('时间(n)'); ylabel('幅度x(n)'); 输出：
实例2： 代码： %用zeros函数和抽样点直接赋值来产生单位抽样序列：范围从-5到5 n0=0; n1=-5;n2=5; n=n1:n2; x=zeros(1,length(n));%生成离散信号x(n) x(n0-(n1)+1)=1;%于n0处产生冲激 stem(n,x,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([n1,n2,0,1.1*max(x)]) %确定横坐标和纵坐标的取值范围 title('单位脉冲序列'); xlabel('时间(n)'); ylabel('幅度x(n)'); 输出同上

2)单位阶跃序列

单位阶跃序列的表示式为 实例1： 代码： %用MATLAB的关系运算式来产生单位阶跃序列u(n)。 n0=0; n1=-5;n2=5; n=n1:n2; x= n>=n0;%于n0处产生冲激 stem(n,x,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([n1,n2,0,1.1*max(x)]) %确定横坐标和纵坐标的取值范围 title('单位阶跃序列'); xlabel('时间(n)'); ylabel('幅度x(n)'); 输出：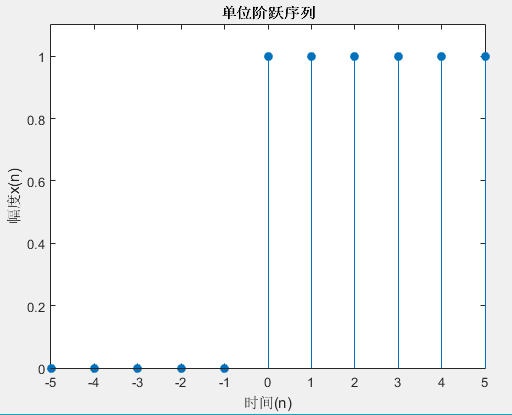
实例2： 代码： %用zeros和ones函数来产生单位阶跃序列u(n)。 n0=0; n1=-5;n2=5; n=n1:n2; x=[zeros(1,n0-n1),ones(1,n2-n0+1)];%于n0处产生冲激 stem(n,x,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([n1,n2,0,1.1*max(x)]) %确定横坐标和纵坐标的取值范围 title('单位阶跃序列'); xlabel('时间(n)'); ylabel('幅度x(n)'); 输出同上

3)实指数序列

实指数序列的表示式为其中a为实数。 当|a|<1时，x(n)的幅度随n的增大而减小，序列逐渐收敛； 当|a|>1时，x(n)的幅度随n的增大而增大，序列逐渐发散。 实例1： 代码： %产生a＝1/2和a＝2实指数连续信号和离散序列 n1=-10;n2=10; a1=0.5;a2=2; x1=a1.^(n1:0); x2=a2.^(0:n2); subplot(2,2,1),plot(n1:0,x1); title('实指数原信号(a<1)'); xlabel('时间(n)'); ylabel('幅度x(n)'); subplot(2,2,2),plot(0:n2,x2); title('实指数原信号(a>1)'); xlabel('时间(n)'); ylabel('幅度x(n)'); subplot(2,2,3),stem(n1:0,x1); title('实指数原信号(a<1)'); xlabel('时间(n)'); ylabel('幅度x(n)'); subplot(2,2,4),stem(0:n2,x2); title('实指数原信号(a>1)'); xlabel('时间(n)'); ylabel('幅度x(n)'); 输出：

4)复指数序列

复指数序列的表示式为: 当w＝0时，x(n)为实指数序列；当s＝0时，x(n)为虚指数序列，即 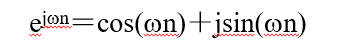　 由上式可知，其实部为余弦序列，虚部为正弦序列。 实例： 代码： %产生alpha＝-0.1,w=0.6的复指数连续信号 alpha=-0.1;w=0.6; n=-10:10; y=exp((alpha+j*w)*n); subplot(2,1,1),plot(n,real(y)); title('实部') subplot(2,1,2),plot(n,imag(y)); title('虚部') 输出：

4.例题

1）已知一时域周期性正弦信号的频率为1 Hz，振幅值幅度为1 V。在窗口上显示2个周期的信号波形，并对该信号的一个周期进行32点采样获得离散信号。试显示原连续信号和其采样获得的离散信号波形。 代码： f=1;%输入信号频率 Um=1;%振幅 nt=2;%显示周期数 N=32;%信号一个周期的采样点数 T=1/f;%信号周期 dt=T/N;%采样时间间隔 n=0:dt:2*N-1; x=Um*sin(2*pi*f*n); subplot(2,1,1),plot(n,x) axis([0,2*T,-1.1*Um,1.1*Um]) subplot(2,1,2),stem(n,x) axis([0,2*T,-1.1*Um,1.1*Um]) 输出：
2)一个连续的周期性矩形波信号频率为5 kHz，信号幅度在0～2 V之间，脉冲宽度与周期的比例为1∶4，且要求在窗口上显示其2个周期的信号波形，并对信号的一个周期进行16点采样来获得离散信号。试显示原连续信号和其采样获得的离散信号波形。 代码： f=5000;%输入信号频率 nt=2;%显示周期数 N=16;%信号一个周期的采样点数 T=1/f;%信号周期 dt=T/N;%采样时间间隔 n=0:dt:nt*N-1; x=square(2*pi*f*n,25)+1; subplot(2,1,1),plot(n,x) axis([0,2*T,0,2.1]) subplot(2,1,2),stem(n,x) axis([0,2*T,0,2.1]) 输出：
有点奇怪，生成的方波是 梯形的？！！