class="markdown_views prism-github-gist">
现研究一连续信号进行抽样转换为数字信号,经数字信号处理器(

其中采样/保持电路和
其中为抽样的周期。那么模拟信号经理想抽样后得到的抽样信号为
设信号的傅里叶变换为,并且其最高频率为,现研究抽样信号的傅里叶变换。
其中。 从上式中就可以看出抽样信号的频谱是原信号频谱的周期延拓。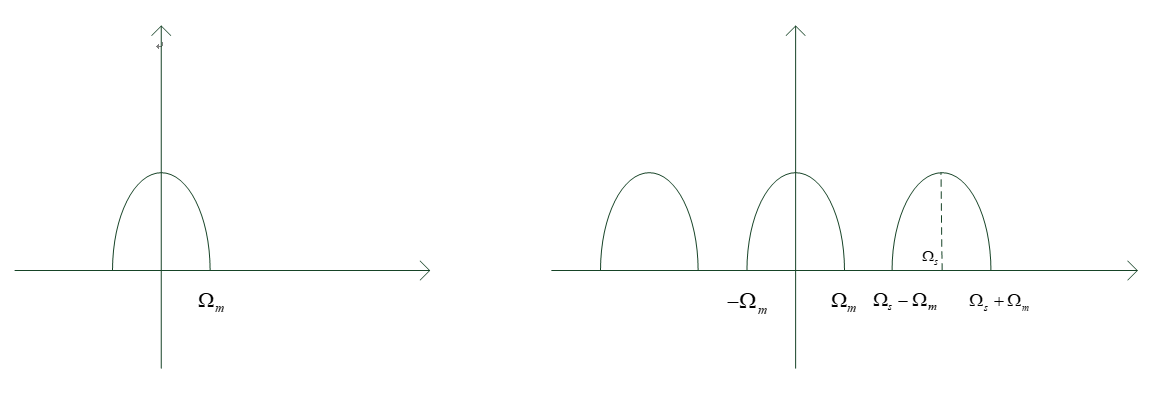 要保证频谱在周期延拓时不发生混叠,那么就要求
要保证频谱在周期延拓时不发生混叠,那么就要求
把称为奈奎斯特采样频率,这是频谱不发生混叠允许的最小采样频率,此时可以通过一低通滤波器将信号恢复出来,若频谱发生了混叠,则很难将信号重建出来。 考虑信号的重建,由频谱图可知,通过一低通滤波器即可将信号完全的恢复出来,假设以频率进行抽样,考虑这么一个低通滤波器:
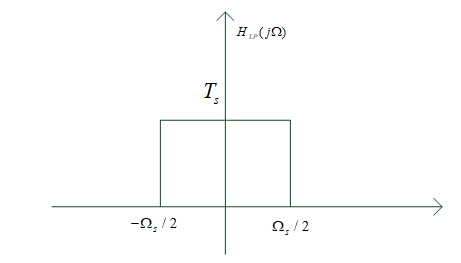
其傅里叶反变换为
其中 由频谱关系知
所以
DSP)或计算机处理后,再进行重建的过程,具体过程如下:

A/D转换电路可以看做是一个理想抽样的过程,而D/A转换和平滑录播可以看做是一个理想内插的过程。
假设理想抽样信号为其中为抽样的周期。那么模拟信号经理想抽样后得到的抽样信号为
设信号的傅里叶变换为,并且其最高频率为,现研究抽样信号的傅里叶变换。
其中。 从上式中就可以看出抽样信号的频谱是原信号频谱的周期延拓。
 要保证频谱在周期延拓时不发生混叠,那么就要求
要保证频谱在周期延拓时不发生混叠,那么就要求把称为奈奎斯特采样频率,这是频谱不发生混叠允许的最小采样频率,此时可以通过一低通滤波器将信号恢复出来,若频谱发生了混叠,则很难将信号重建出来。 考虑信号的重建,由频谱图可知,通过一低通滤波器即可将信号完全的恢复出来,假设以频率进行抽样,考虑这么一个低通滤波器:
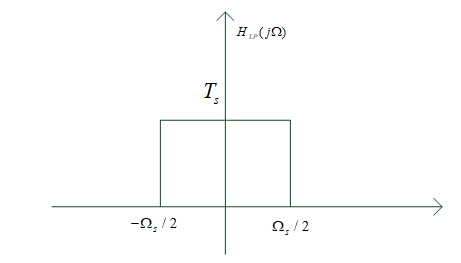
其中 由频谱关系知
所以