版权声明:转载请注明出处 https://blog.csdn.net/weixin_42183571/article/details/80615660
概述
ANC,英文名称:Active Noise Control,主动降噪。其原理是降噪系统电路产生降噪MIC接收的外界环境噪音相等的反相信号,将噪声抵消。
核心算法
ANC降噪实现核心算法为:FxLMS(最小均方差算法)。最小均方差算法以均方误差为代价函数,并使误差降到最小的算法。 具体算法推导这里不做具体介绍,这里直接列出表达式:
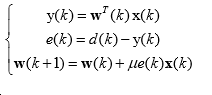 其中, x(k)为输入信号矩阵,W(k)为调整权值矩阵,d(k)为目标(理想)输出信号矩阵,y(k)为实际输出信号矩阵,e(k)为误差信号矩阵,第3个公式为权值调整公式,mu为收敛因子(值为随机的,0
其中, x(k)为输入信号矩阵,W(k)为调整权值矩阵,d(k)为目标(理想)输出信号矩阵,y(k)为实际输出信号矩阵,e(k)为误差信号矩阵,第3个公式为权值调整公式,mu为收敛因子(值为随机的,0Matlab仿真LMS滤波器
根据表达式设计滤波器

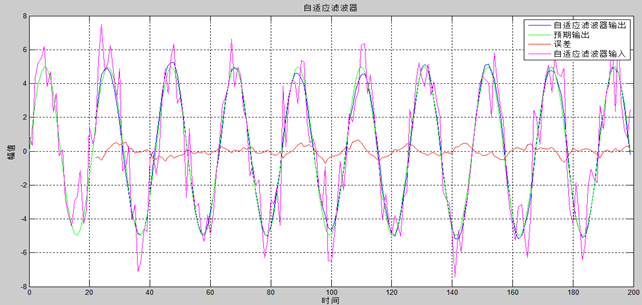
 结果分析
输入信号为正弦信号加噪声的混合信号,可见正弦信号受噪声影响失真较大;实验输出信号失真较小,噪声信号已经很小,这里可以调节M滤波器阶数来调节ANC降噪效果。可见,LMS算法可实现ANC降噪功能。
实际应用分析
实际应用中,ANC降噪对2KHZ以下的信号噪声降噪效果比较好,对高频噪声降噪效果很差。原因为高频信号波长短,对相位偏差也比较敏感,导致ANC对高频噪声降噪效果差。一般高频噪声可以被耳机物理的遮蔽屏蔽掉,这种降噪被称为被动降噪。 总结,一般2KHz噪声信号使用ANC,高频信号没有必要使用ANC。实际测试中的应用,测试步骤:1.关闭ANC时,声学测试软件测试声学参数FR;2.打开ANC时,声学测试软件测试声学参数FR,这里通过调节gain值,来调节降噪效果,使降噪效果适中。因为降噪效果差,达不到降噪的目的;降噪效果如果太好,噪声信号趋近于0,会使耳机产生自激。
通过书籍资料及网上资源学习,以上就是我对ANC的理解,如有什么不妥之处,还请指正。
结果分析
输入信号为正弦信号加噪声的混合信号,可见正弦信号受噪声影响失真较大;实验输出信号失真较小,噪声信号已经很小,这里可以调节M滤波器阶数来调节ANC降噪效果。可见,LMS算法可实现ANC降噪功能。
实际应用分析
实际应用中,ANC降噪对2KHZ以下的信号噪声降噪效果比较好,对高频噪声降噪效果很差。原因为高频信号波长短,对相位偏差也比较敏感,导致ANC对高频噪声降噪效果差。一般高频噪声可以被耳机物理的遮蔽屏蔽掉,这种降噪被称为被动降噪。 总结,一般2KHz噪声信号使用ANC,高频信号没有必要使用ANC。实际测试中的应用,测试步骤:1.关闭ANC时,声学测试软件测试声学参数FR;2.打开ANC时,声学测试软件测试声学参数FR,这里通过调节gain值,来调节降噪效果,使降噪效果适中。因为降噪效果差,达不到降噪的目的;降噪效果如果太好,噪声信号趋近于0,会使耳机产生自激。
通过书籍资料及网上资源学习,以上就是我对ANC的理解,如有什么不妥之处,还请指正。
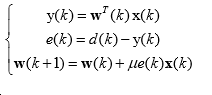 其中, x(k)为输入信号矩阵,W(k)为调整权值矩阵,d(k)为目标(理想)输出信号矩阵,y(k)为实际输出信号矩阵,e(k)为误差信号矩阵,第3个公式为权值调整公式,mu为收敛因子(值为随机的,0
其中, x(k)为输入信号矩阵,W(k)为调整权值矩阵,d(k)为目标(理想)输出信号矩阵,y(k)为实际输出信号矩阵,e(k)为误差信号矩阵,第3个公式为权值调整公式,mu为收敛因子(值为随机的,0-
function [yn,W,en]=LMS(xn,dn,M,mu,itr) -
% LMS(Least Mean Squre)算法 -
% 输入参数: -
% xn 输入的信号序列 (列向量) -
% dn 所期望的响应序列 (列向量) -
% M 滤波器的阶数 (标量) 滤波器的阶数,就是指过滤谐波的次数,其阶数越高,滤波效果就越好 -
% mu 收敛因子(步长) (标量) 要求大于0,小于xn的相关矩阵最大特征值的倒数 -
% itr 迭代次数 (标量) 默认为xn的长度,M -
% 输出参数: -
% W 滤波器的权值矩阵 (矩阵) -
% 大小为M : itr, -
% en 误差序列(itr : 1) (列向量) -
% yn 实际输出序列 (列向量) -
% 参数个数必须为4个或5个 -
if nargin == 4 % 4个时递归迭代的次数为xn的长度 -
itr = length(xn); -
elseif nargin == 5 % 5个时满足M -
if itr>length(xn) || itr -
error('迭代次数过大或过小!'); -
end -
else -
error('请检查输入参数的个数!'); -
end -
% 初始化参数 -
en = zeros(itr,1); % 误差序列,en(k)表示第k次迭代时预期输出与实际输入的误差 -
W = zeros(M,itr); % 每一行代表一个加权参量,每一列代表-次迭代,初始为0 -
% 迭代计算 -
for k = M:itr % 第k次迭代 -
x = xn(k:-1:k-M+1); % 滤波器M个抽头的输入 -
y = W(:,k-1).' * x; % 滤波器的输出 -
en(k) = dn(k) - y ; % 第k次迭代的误差 -
% 滤波器权值计算的迭代式 -
W(:,k) = W(:,k-1) + 2*mu*en(k)*x; -
end -
% 求最优时滤波器的输出序列 -
yn = inf * ones(size(xn)); -
for k = M:length(xn) -
x = xn(k:-1:k-M+1); -
yn(k) = W(:,end).'* x; -
end
-
close all -
% 正弦信号的产生 -
t=0:199; -
xs=5*sin(0.3*t); -
figure; -
subplot(2,1,1); -
plot(t,xs);grid; -
ylabel('幅值'); -
title('{输入正弦波信号}'); -
% 随机噪声信号的产生 -
randn('state',sum(100*clock)); -
xn=randn(1,200); -
zn=randn(1,200); -
xn=xn+zn; -
subplot(2,1,2); -
plot(t,xn);grid; -
ylabel('幅值'); -
xlabel('时间'); -
title('{输入随机噪声信号}'); -
% 信号滤波 -
xn = xs+xn; -
xn = xn.' ; % 输入信号序列 -
dn = xs.' ; % 预期理想结果序列 -
M = 23 ; % 滤波器的阶数 -
rho_max = max(eig(xn*xn.')); % 输入信号相关矩阵的最大特征值 -
mu = rand()*(1/rho_max) ; % 收敛因子 0 < mu < 1/rho_max -
[yn,W,en] = LMS(xn,dn,M,mu); -
% 绘制滤波器输入信号 -
figure; -
subplot(2,1,1); -
plot(t,xn);grid; -
ylabel('幅值'); -
xlabel('时间'); -
title('{滤波器输入信号}'); -
% 绘制自适应滤波器输出信号 -
subplot(2,1,2); -
plot(t,yn);grid; -
ylabel('幅值'); -
xlabel('时间'); -
title('{自适应滤波器输出信号}'); -
% 绘制自适应滤波器输出信号,预期输出信号和两者的误差 -
figure -
plot(t,yn,'b',t,dn,'g',t,dn-yn,'r',t,xn,'m');grid; -
legend('自适应滤波器输出','预期输出','误差','自适应滤波器输入'); -
ylabel('幅值'); -
xlabel('时间'); -
title('{自适应滤波器}'); -
%绘制最优权值点 -
figure -
mm=0:M-1; -
plot(mm,W(:,end)','m*');grid; -
title('{最优权值点}');


 结果分析
输入信号为正弦信号加噪声的混合信号,可见正弦信号受噪声影响失真较大;实验输出信号失真较小,噪声信号已经很小,这里可以调节M滤波器阶数来调节ANC降噪效果。可见,LMS算法可实现ANC降噪功能。
实际应用分析
实际应用中,ANC降噪对2KHZ以下的信号噪声降噪效果比较好,对高频噪声降噪效果很差。原因为高频信号波长短,对相位偏差也比较敏感,导致ANC对高频噪声降噪效果差。一般高频噪声可以被耳机物理的遮蔽屏蔽掉,这种降噪被称为被动降噪。 总结,一般2KHz噪声信号使用ANC,高频信号没有必要使用ANC。实际测试中的应用,测试步骤:1.关闭ANC时,声学测试软件测试声学参数FR;2.打开ANC时,声学测试软件测试声学参数FR,这里通过调节gain值,来调节降噪效果,使降噪效果适中。因为降噪效果差,达不到降噪的目的;降噪效果如果太好,噪声信号趋近于0,会使耳机产生自激。
通过书籍资料及网上资源学习,以上就是我对ANC的理解,如有什么不妥之处,还请指正。
结果分析
输入信号为正弦信号加噪声的混合信号,可见正弦信号受噪声影响失真较大;实验输出信号失真较小,噪声信号已经很小,这里可以调节M滤波器阶数来调节ANC降噪效果。可见,LMS算法可实现ANC降噪功能。
实际应用分析
实际应用中,ANC降噪对2KHZ以下的信号噪声降噪效果比较好,对高频噪声降噪效果很差。原因为高频信号波长短,对相位偏差也比较敏感,导致ANC对高频噪声降噪效果差。一般高频噪声可以被耳机物理的遮蔽屏蔽掉,这种降噪被称为被动降噪。 总结,一般2KHz噪声信号使用ANC,高频信号没有必要使用ANC。实际测试中的应用,测试步骤:1.关闭ANC时,声学测试软件测试声学参数FR;2.打开ANC时,声学测试软件测试声学参数FR,这里通过调节gain值,来调节降噪效果,使降噪效果适中。因为降噪效果差,达不到降噪的目的;降噪效果如果太好,噪声信号趋近于0,会使耳机产生自激。
通过书籍资料及网上资源学习,以上就是我对ANC的理解,如有什么不妥之处,还请指正。