今天翻书正好翻到这个,就把一些想法给记录下来,免得以后又忘记自己当初是怎么想的。
Δf 的定义是
Δf=1NTS=1T
其中Ts=1fs 为采样周期,N 时域为窗口长度(点数),T=NTs=Nfs 为时域采样时间长度。
通俗的说频率分辨率就是你在一条直线(频率轴)上画竖线,相邻的两个竖线之间的间隔(你要分得清这两根线,不能黑乎乎的黏在一起)就是频率分辨率了,这种线画得越多频率分辨率自然就越高。
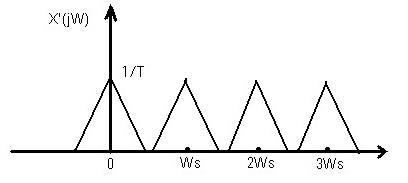
然后我们对原信号以fs 的频率进行采样,那么对应到频域上就是卷积以fs 为间隔的冲激串,如图所示:
这里插入一个证明,就是在时域上进行N点的采样,DFT对应到频域上也是N点的采样:
将频域信号转化为有限长离散信号。与对时域信号的处理类似,经过离散化,即可得到有限长离散信号。设时域信号限于[0, T]时,采样周期为Ts ,则时域采样点数N=TTs 。依据采样定理,时域采样若要能完全重建原信号,频域信号应当带限于(0,12∗Ts ),由采样定理以及时频对偶的关系,频域的采样间隔应为1T 。故,频域采样点数为:
1/T1/L=N
即频域采样的点数和时域采样同为N。
然后回归正题,如果我们对一开始的那段信号在时域上一共采样了N个点,也就是说对刚刚得到的CTFT在[0,fs ]上进行N个点采样,那么得到的就是我们的结果频率分辨率Δf 了
Δf=1NTS
物理含义也很清晰,就是频域上两个频率成分之间的间隔。值得注意的是Δf 越小,反而说明频率分辨率越高。
好了,那么第二个等号是什么物理含义呢?
Δf=1T
就是连续信号的信号长度越长(时间分辨率越低),频率分辨率越好,又是一个对偶的属性!这个的物理含义一开始我也是想得不是太明白,不过我的一个同学给了一个不错的解释,大家可以参考一下:
长度为T的一段信号因为是连续的,比较难想象,我们不妨将它转换为离散的,也就是说我们将它看成N个点的一段信号。这段信号的N越长,就意味着信号对应到频域上的点数越多,那Δf 自然是越小啦。
这里也有一个值得注意的地方,就是如果长度固定了,就是说采样率跟采样点数是成反比的,这就不存在说我们增加采样率或者是采样点数会让频率分辨率变好的情况,从公式就可以的出来的结论嘛~
Sa 函数,就有主瓣了,自然就变粗了。所以我们只能在尽量减少主瓣的宽度,这样频率分辨率就会变得更加接近于理想情况(但是绝对不会比原分辨率更好),这就是在用矩形窗的时候所说的提高截断长度可以“提高”频率分辨率(因为矩形窗的窗越长主瓣就越小)。
定义
频率分辨率其中
证明
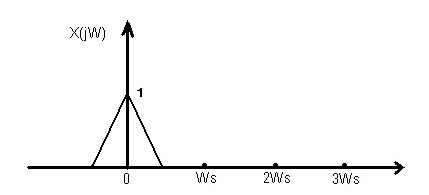
对于这个公式我是这么理解的,首先我们截取信号待处理的区域,得到一段连续非周期信号(虽然计算机里面只能存储离散的信号,可是我们现在先假设为理论的情况),根据对偶定理,可以知道这段信号经过傅里叶变换后会变为一段连续非周期信号。大概就是这样的一个一段信号(假设为带限):
然后我们对原信号以

这里插入一个证明,就是在时域上进行N点的采样,DFT对应到频域上也是N点的采样:
将频域信号转化为有限长离散信号。与对时域信号的处理类似,经过离散化,即可得到有限长离散信号。设时域信号限于[0, T]时,采样周期为
即频域采样的点数和时域采样同为N。
然后回归正题,如果我们对一开始的那段信号在时域上一共采样了N个点,也就是说对刚刚得到的CTFT在[0,
物理含义也很清晰,就是频域上两个频率成分之间的间隔。值得注意的是
好了,那么第二个等号是什么物理含义呢?
就是连续信号的信号长度越长(时间分辨率越低),频率分辨率越好,又是一个对偶的属性!这个的物理含义一开始我也是想得不是太明白,不过我的一个同学给了一个不错的解释,大家可以参考一下:
长度为T的一段信号因为是连续的,比较难想象,我们不妨将它转换为离散的,也就是说我们将它看成N个点的一段信号。这段信号的N越长,就意味着信号对应到频域上的点数越多,那