增采样与减采样

普通DSP课本里可能没有增采样和减采样的内容。有些大学的DSP课程内容比较深。相信，很多包括通信专业的学生对于信号处理的精髓不是很明白。下面分析一下这个增采样过程。
大家知道采样的原理是：X(n)=Xc(t)|t=nT =Xc(nT). Xc(t)是连续时间信号。x(n)是相应的离散时间信号。T是采样率。Xc(Ω)是Xc(t)的连续时间傅里叶变换。 X（ΩT)=1T(∑k=0∞Xc(Ω−k2πT)) X(w)=1T(∑k=0∞Xc(wT−k2πT))

---

The truth of sampling

采样的实质是什么？模拟频率Ω到数字频率w。
数字频率w，指的是采样点之间的弧度，一般|w|<=π。若采用w，exp(jw)在单位圆上，光于2π的周期性离散信号周期为2π。由此我们不用计算就可以证明就能得到奈奎斯特定理。y(t) = sin(Ωt)，w = Ω/T; 对于信号y(t)的最大频域截止Ω = π/T。为了不尝生混迭， Ωs = 2π/T。故Ωs = 2Ω ；

upsampling

在没有经过滤波器之前是这样的： xi[n]=xc(nT′);T′=T/L;xi[n]=x[n/L]=xc(nT/L) 当n=kL(k为整数),xe[n]=x[n/L]=∑k=−∞∞x[k]δ[n−kL] 其他情况，xe[n]=0; Xe(ejw)=∑n=−∞∞(∑k=−∞∞x[k]δ[n−kL])e−jwn=∑k=−∞∞x[k]e−jwkL=X(ejwL) 维基百科有这样的说明。点此进入查看upsampling;
类似的推导之后：

---

downsampling

点此进入查看downsampling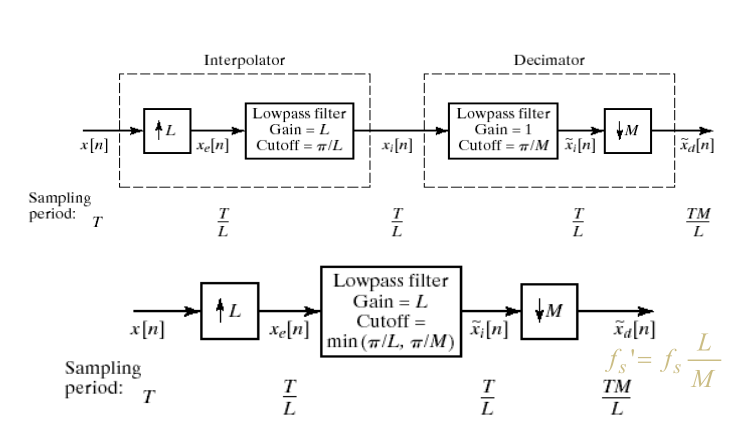 Xd（ejw)=1M(∑i=0M−1X(ewM−2πiM)
[这是奥本海默的DSP里的一张图] 然而有些人可能不明白为什么这里的增采样之后，只是填充零，为什么会在幅度上引起L的变化。根据帕斯瓦尔定理，能量是不变的，因为0是没有能量的。采样导致频率周期性，低通滤波器，把频域上中间那段取出来了，能量降低为1/I*I ,为了恢复想x(0),低通滤波器增益为I。下面是MATLAB的仿真说明。 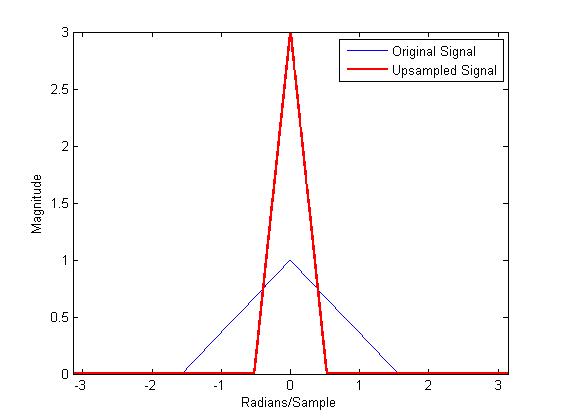增采样之后滤波后的幅度变化。。
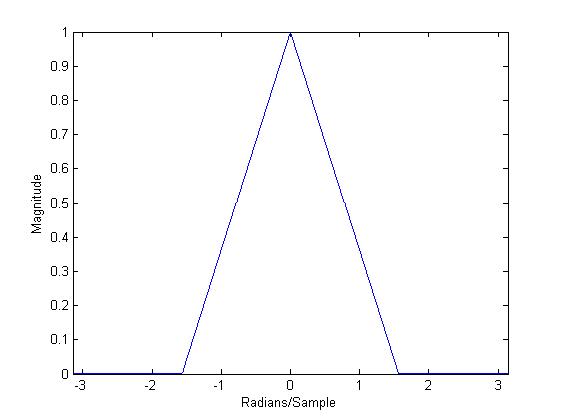
matlab代码： F = [0 0.250 0.500 0.7500 1]; A = [1.0000 0.5000 0 0 0]; Order = 511; B = fir2(Order,F,A); [Hx,W] = freqz(B,1,8192,'whole'); Hx = [Hx(4098:end) ; Hx(1:4097)]; omega = -pi+(2*pi/8192):(2*pi)/8192:pi; plot(omega,abs(Hx)) xlim([-pi pi]) xlabel('Radians/Sample') ylabel('Magnitude') F = [0 0.250 0.500 0.7500 1]; A = [1.0000 0.5000 0 0 0]; Order = 511; B = fir2(Order,F,A); [Hx,W] = freqz(B,1,8192,'whole'); Hx = [Hx(4098:end) ; Hx(1:4097)]; omega = -pi+(2*pi/8192):(2*pi)/8192:pi; plot(omega,abs(Hx)) xlim([-pi pi]) xlabel('Radians/Sample') ylabel('Magnitude') y = interp(B,2); [Hy,W] = freqz(y,1,8192,'whole'); Hy = [Hy(4098:end) ; Hy(1:4097)]; hold on 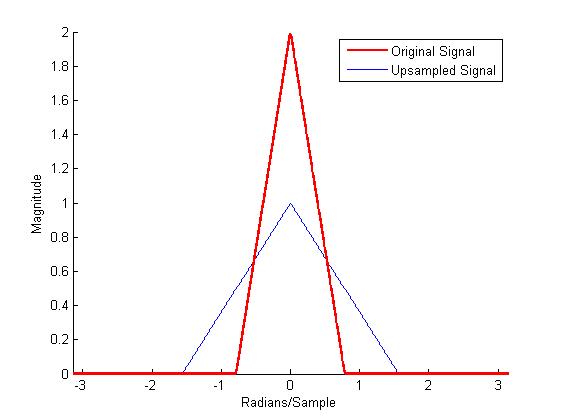plot(omega,abs(Hy),'r','linewidth',2) legend('Original Signal','Upsampled Signal')
“`