DSP

交换排序之冒泡排序优化源码及时间复杂度

2019-07-13 17:04发布

站内文章 / DSP
14686 0 1427
常见的交换排序包括冒泡排序和快速排序。 用于显示的代码：show.cpp #include using namespace std; template <class T> void showww(T* t, int n) { for(int i=0; icout << *(t+i) << endl; }

冒泡排序

bubble.cpp template <class T> int bubble_sort(T* t, int n) { int camp_times = 0; for(int j=0; j1; j++) { for(int k=j+1; kif(t[j] > t[k]) { T tmp = t[j]; t[j] = t[k]; t[k] = tmp; } } } return camp_times; } 主函数： #include "bubble.cpp" #include "show.cpp" int main() { double num[] = {1.2, 4.55, 2.34, 56.56, 78.3, -23.5, 9.8}; int numi[] = {1, 2, 3, 4, 5, 6, 7}; int n = 7; cout << "--------------before-------------- "; showww(num, n); int campare_times = bubble_sort(num,n); cout << "--------------after-------------- "; showww(num,n); cout << "---------compare_times: " << campare_times << "--------- " << endl; cout << "--------------before-------------- "; showww(numi, n); campare_times = bubble_sort(numi,n); cout << "--------------after-------------- "; showww(numi,n); cout << "---------compare_times: " << campare_times << "---------" << endl; return 0; } 执行结果：
这里写图片描述

时间复杂度

o(n2)

空间复杂度

o(1)
空间复杂度不受问题规模影响，为就地排序。

优化后的冒泡排序

优化原理：当某一次排序不再发生冒泡（大小交换）时，说明已经有序了，则不再进行下一轮排序。
最好的情况下(排序前就已经有序)，时间复杂度为：
o(n)
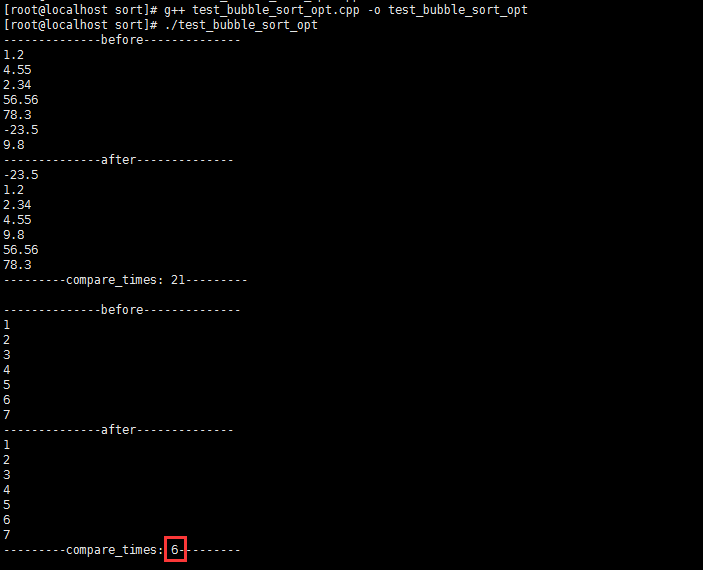
bubble_sort.cpp template <class T> int bubble_sort(T* t, int n) { int camp_times = 0; bool exchange = false; for(int j=0; j1; j++) { for(int k=j+1; kif(t[j] > t[k]) { T tmp = t[j]; t[j] = t[k]; t[k] = tmp; exchange = true; } } if(!exchange) break; } return camp_times; } 执行结果：
这里写图片描述

热门文章