class="markdown_views prism-github-gist">
 程序
程序

后来对应程序也许有个更好的函数, 思路,先用residuez或者residue算出留数和极点,但是此时会发现其中有些是复数共轭的形式,对于复数共轭的形式需要再利用residuez或者residue,然后取实,算出对应框图的系数.
程序
思路,先用residuez或者residue算出留数和极点,但是此时会发现其中有些是复数共轭的形式,对于复数共轭的形式需要再利用residuez或者residue,然后取实,算出对应框图的系数.
程序
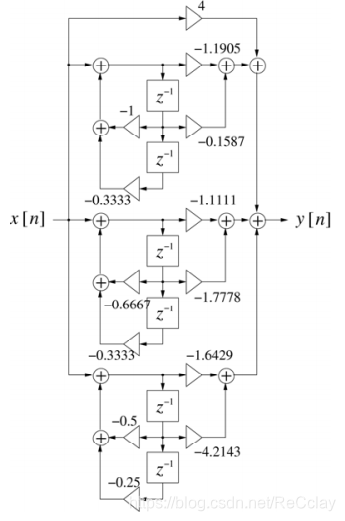 并联II
并联II

一、生成如下因果无限冲激响应传输函数的级联实现,画出级联实现的结构图。
 程序
程序
clc;
clear;
format rat;
num = input('分子系数向量 = ');
den = input('分母系数向量 = ');
[z,p,k] = tf2zp(num,den);%由传递函数转换为零极点增益
sos = zp2sos(z,p,k)%由零极点增益转换为二次分式
过程及结果
分子系数向量 = [3 8 12 7 2 -2]
分母系数向量 = [16 24 24 14 5 1]
sos =
3/16 -1/16 0 1 1/2 0
1 2 2 1 1/2 1/4
1 1 1 1 1/2 1/2
对应框图
后来对应程序也许有个更好的函数,
clc;
clear;
format rat;
num = input('分子系数向量 = ');%[3 8 12 7 2 -2]
den = input('分母系数向量 = ');%[16 24 24 14 5 1]
[sos g] = tf2sos(num,den)%由传递函数转换为零极点增益
过程及结果
分子系数向量 = [3 8 12 7 2 -2]
分母系数向量 = [16 24 24 14 5 1]
sos =
1 -1/3 0 1 1/2 0
1 2 2 1 1/2 1/4
1 1 1 1 1/2 1/2
g =
3/16
好在何方呢?
增益和系数分离,对应系数就直接就是框图系数了,增益在整个框图最前面!!!
二、生成如下因果无限冲激响应传输函数的并联实现,画出并联实现的结构图。
 思路,先用residuez或者residue算出留数和极点,但是此时会发现其中有些是复数共轭的形式,对于复数共轭的形式需要再利用residuez或者residue,然后取实,算出对应框图的系数.
程序
思路,先用residuez或者residue算出留数和极点,但是此时会发现其中有些是复数共轭的形式,对于复数共轭的形式需要再利用residuez或者residue,然后取实,算出对应框图的系数.
程序
clc;
clear;
format short;
num = input('分子系数向量 = ');%[2 10 23 34 31 16 4]
den = input('分母系数向量 = ');%[36 78 87 59 26 7 1]
[r1,p1,k1] = residuez(num,den);
[r2,p2,k2] = residue(num,den);
disp('并联 I')
disp('留数:');disp(r1);
disp('极点:');disp(p1);
disp('常量:');disp(k1);
disp('并联 II')
disp('留数:');disp(r2);
disp('极点:');disp(p2);
disp('常量:');disp(k2);
disp('并联I 的复共轭对,对应框图系数');
disp('并联I-First:');
R1 = [r1(1) r1(2)];P1 = [p1(1) p1(2)];
[b1 a1] = residuez(R1, P1, 0);%并联I用residuez
disp('分子');disp(real(b1));
disp('分母');disp(real(a1));
disp('并联I-Second:');
R1 = [r1(3) r1(4)];P1 = [p1(3) p1(4)];
[b1 a1] = residuez(R1, P1, 0);%并联I用residuez
disp('分子');disp(real(b1));
disp('分母');disp(real(a1));
disp('并联I-Third:');
R1 = [r1(5) r1(6)];P1 = [p1(5) p1(6)];
[b1 a1] = residuez(R1, P1, 0);%并联I用residuez
disp('分子');disp(real(b1));
disp('分母');disp(real(a1));
disp('并联II 的复共轭对,对应框图系数');
disp('并联II-First:');
R2 = [r2(1) r2(2)];P2 = [p2(1) p2(2)];
[b2 a2] = residue(R2, P2, 0);%并联II用residue
disp('分子');disp(real(b2));
disp('分母');disp(real(a2));
disp('并联II-Second:');
R2 = [r2(3) r2(4)];P2 = [p2(3) p2(4)];
[b2 a2] = residue(R2, P2, 0);%并联II用residue
disp('分子');disp(real(b2));
disp('分母');disp(real(a2));
disp('并联II-Third:');
R2 = [r2(5) r2(6)];P2 = [p2(5) p2(6)];
[b2 a2] = residue(R2, P2, 0);%并联II用residue
disp('分子');disp(real(b2));
disp('分母');disp(real(a2));
注意,并联I 用residuez;并联II 用residue…
过程及结果
分子系数向量 = [2 10 23 34 31 16 4]
分母系数向量 = [36 78 87 59 26 7 1]
并联 I
留数:
-0.5556 - 2.2785i
-0.5556 + 2.2785i
-0.5952 - 0.7561i
-0.5952 + 0.7561i
-0.8214 + 4.3920i
-0.8214 - 4.3920i
极点:
-0.3333 + 0.4714i
-0.3333 - 0.4714i
-0.5000 + 0.2887i
-0.5000 - 0.2887i
-0.2500 + 0.4330i
-0.2500 - 0.4330i
常量:
4
并联 II
留数:
1.2593 + 0.4976i
1.2593 - 0.4976i
0.5159 + 0.2062i
0.5159 - 0.2062i
-1.6964 - 1.4537i
-1.6964 + 1.4537i
极点:
-0.3333 + 0.4714i
-0.3333 - 0.4714i
-0.5000 + 0.2887i
-0.5000 - 0.2887i
-0.2500 + 0.4330i
-0.2500 - 0.4330i
常量:
0.0556
并联I 的复共轭对,对应框图系数
并联I-First:
分子
-1.1111 1.7778 0
分母
1.0000 0.6667 0.3333
并联I-Second:
分子
-1.1905 -0.1587 0
分母
1.0000 1.0000 0.3333
并联I-Third:
分子
-1.6429 -4.2143 0
分母
1.0000 0.5000 0.2500
并联II 的复共轭对,对应框图系数
并联II-First:
分子
2.5185 0.3704
分母
1.0000 0.6667 0.3333
并联II-Second:
分子
1.0317 0.3968
分母
1.0000 1.0000 0.3333
并联II-Third:
分子
-3.3929 0.4107
分母
1.0000 0.5000 0.2500
并联I
 并联II
并联II
