class="markdown_views prism-atom-one-light"> 注：本文是程序的说明和实现思路，代码见：https://download.csdn.net/download/hnxyxiaomeng/10301718 一、主要思路
原始信号：OrgSig
信号长度：DWT_SIG_LEN
小波分解层数：N
与MATLAB类似，小波分解后产生2个数组DWT_L和DWT_C，但定义与MATLAB不同。定义如下：
DWT_L：[DWT_SIG_LEN,cD1_LEN,cD2_LEN…,cDN_LEN]，其中xxx_LEN代表该数组的长度
DWT_C：[cD1 | cD2 | … cDN | cAN]，其中cDx代表第x层的细节系数，cAN代表第N层的近似系数
二、函数原型
1、 小波变换函数DWT_Dwt
函数原型： /**************************************** **小波变换，即1层小波分解 //V1.00 实现基本功能 2016-9-18 21:41:50 * @原理： DWT_FILTER_LEN-1 1、cA(n) = ∑ DWT_Lo_D[k]*Sig[2*n-k+1] k=0 2、上述公式实现了卷积后再降采样，并且降采样时采的是第偶数个点 3、Sig的下标加1就是为了保证采样的是偶数点（C中下标从0开始，偶数点是第1，3，5....），若不加1，则采的是奇数点 4、cD(n)的实现原理同上 5、信号边沿采用对称延拓 * @return正常则返回变换后近似系数和细节系数的长度，错误则返回0 *****************************************/ uint16_t DWT_Dwt( float32_t* p_OrgSig, //原始信号 uint16_t OrgSigLen, //信号长度 float32_t *cA, //近似系数 float32_t *cD //细节系数 ) 2、 小波逆变换函数DWT_Idwt /**************************************** **小波逆变换，即1层小波重构 //V1.00 实现基本功能 2016-9-18 14:48:24 * @原理： cA_LEN-1 1、Sig(n) = ∑ DWT_Lo_R[n-2*k + DWT_FILTER_LEN -2]*cA[k] + DWT_Hi_R[n-2*k + DWT_FILTER_LEN -2]*cD[k] k=0 2、上述公式实现了升采样后卷积，然后再相加 * @return 正常则返回逆变换后信号的长度，错误则返回0 *****************************************/ uint16_t DWT_Idwt( float32_t *cA, //近似系数 float32_t *cD, //细节系数 uint16_t cALen, //系数长度 uint16_t recLen, //重构的信号长度 float32_t* p_OrgSig //重构的信号 ) 3、 小波分解函数DWT_WaveDec
函数原型： /**************************************** **小波分解，可实现N层小波分解 //V1.00 实现基本功能 2016-10-8 10:14:56 * @原理： 1、逐层调用DWT_Dwt函数进行小波变换 2、建立临时变量DWT_temp0和DWT_temp1用于存储各层变换中临时产生的近似变量 3、将cD1~cDN和cAN依次存入DWT_C中 4、DWT_L已经在变量定义时初始化 * @return 正常则返回1，错误则返回0 *****************************************/ uint16_t DWT_WaveDec( float32_t* p_OrgSig, //原始信号 uint16_t OrgSigLen, //信号长度 uint16_t DecLevel //分解层数 ) 4、 小波重构函数DWT_WaveRec
函数原型： /**************************************** **小波重构，由DWT_L和DWT_C可实现N层小波重构 //V1.00 实现基本功能 2016-10-8 10:25:25 * @原理： 1、从DWT_C中取cD1~cDN和cAN进行逆变换 1、逐层调用DWT_Idwt函数进行小波变换 2、建立临时变量DWT_temp0和DWT_temp1用于存储各层逆变换中临时产生的近似变量 * @return 正常则返回1，错误则返回0 *****************************************/ uint16_t DWT_WaveRec( float32_t* p_C, //DWT_L uint16_t* p_L, //DWT_C uint16_t DecLevel, //小波分解的层数 float32_t* p_OrgSig //重构出的原始信号 ) 三、移植过程
1、 根据算法研究结果，确定需要进行小波分解的信号长度、小波函数和分解层数
2、 修改.h文件
a、修改信号长度、分解层数和小波系数长度 #define DWT_SIG_LEN 30 //信号的长度 #define DWT_DEC_LEVEL 3 //小波分解的层数 #define DWT_FILTER_LEN 6 //小波系数的长度，根据选择小波的不同而不同 b、修改DWT_L中的元素 #define DWT_L1 (DWT_SIG_LEN+DWT_FILTER_LEN-1)>>1 #define DWT_L2 ((DWT_L1)+DWT_FILTER_LEN-1)>>1 #define DWT_L3 ((DWT_L2)+DWT_FILTER_LEN-1)>>1 //#define DWT_L4 ((DWT_L3)+DWT_FILTER_LEN-1)>>1 c、修改DWT_C的长度 #define DWT_C_LEN (DWT_L1)+(DWT_L2)+(DWT_L3 )*2//+(DWT_L2)+(DWT_L3)+(DWT_L4)+(DWT_L5)+(DWT_L6)+(DWT_L7) //数组C的长度 3、 修改.c文件
a、修改DWT_C中的元素 uint16_t DWT_L[DWT_L_LEN] = {DWT_SIG_LEN, DWT_L1, DWT_L2, DWT_L3 };//需要根据DWT_L中元素的声明依次向里添加 b、修改小波系数 //db3 const float32_t DWT_Lo_D[DWT_FILTER_LEN] = { 0.0352, -0.0854, -0.1350, 0.4599, 0.8069, 0.3327}; const float32_t DWT_Hi_D[DWT_FILTER_LEN] = { -0.3327, 0.8069, -0.4599, -0.1350, 0.0854, 0.0352}; const float32_t DWT_Lo_R[DWT_FILTER_LEN] = { 0.3327, 0.8069, 0.4599, -0.1350, -0.0854, 0.0352}; const float32_t DWT_Hi_R[DWT_FILTER_LEN] = { 0.0352, 0.0854, -0.1350, -0.4599, 0.8069, -0.3327}; 4、 使用分解和重构函数
在程序中合适的位置，缓存或预定义一段原始数据OrgSig，并定义另一个与之长度的相同的数组，用于存储重构后的数据。使用例程如下： float32_t OrgSig[DWT_SIG_LEN] = {1, 2, 1, -1, 1, 2, -1, -2, 1, 2, 3, 4, 5, 6, 7, 8, 1, 12, 13, 1, 3, 6, 8, 1, 4, 4, 4, 2, 8, 10}; float32_t OrgSig1[DWT_SIG_LEN] = {0}; DWT_WaveDec( OrgSig, DWT_SIG_LEN, DWT_DEC_LEVEL ); DWT_WaveRec( DWT_C,DWT_L, DWT_DEC_LEVEL,OrgSig1 ); 四、注意事项
1、 堆栈设置问题
小波变换需要的临时变量较大，当信号长度较大时，可能会引起HardFault，进而进入函数HardFault_Handler死循环。这时，需要在启动文件startup_stm32f40_41xxx.s中修改堆区大小。
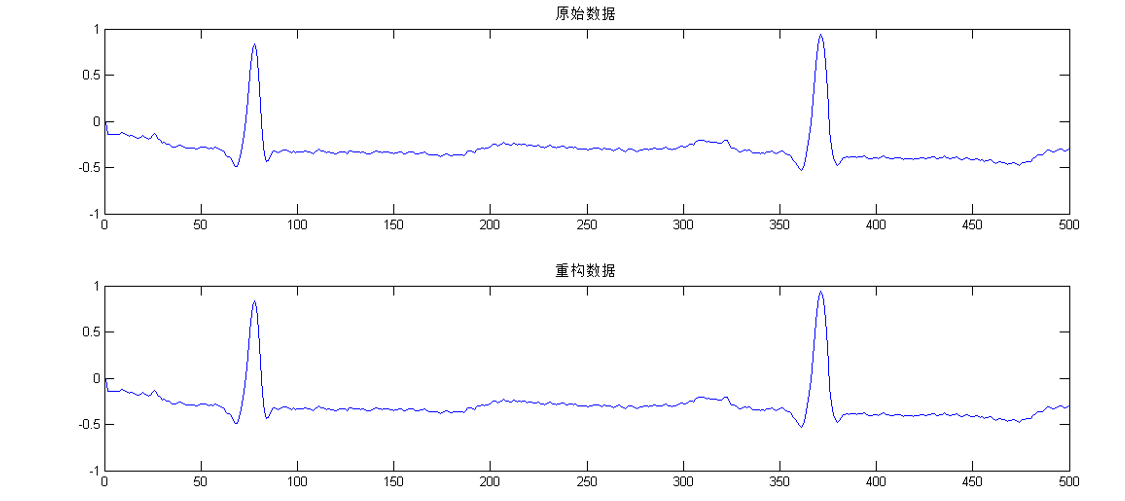
如： ; Stack_Size EQU 0x00000400 //默认设置是这个 Stack_Size EQU 0x0000FF00 五、测试结果
1、 对于采样率为360Hz的ECG信号，利用db3对500个点进行4层小波分解后再重构，得到结果对比如下图，二者相关系数为1.0000。
六、说明
程序为原创，文章是程序的说明。