原文链接:
最近实习的时候,发现自己的 DSP 基本功还是不够扎实,关于模拟/数字角频率,频率,采样速率等一些概念理解的都不太深刻,愧对老师和这么多年的学习,Google 到一些讲解的比较清楚的 blog,备忘(抄袭)过来,温故而知新。
首先从最基本的三角函数的定义开始: 三角函数的定义方式有很多种,我觉得基于单位圆的定义是最形象,对之后理解各种角频率的物理/数学含义最有帮助。 我们应该是在初中的时候第一次接触到三角函数,那时候三角函数的定义是直接给个三角形,然后直接定义 sin(cos) 为哪条边比哪条边的值,然后给出 sin(cos) 的波形如下图所示: "Sine cosine one period" by Geek3 - Own work.
Licensed under CC BY 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Sine_cosine_one_period.svg#/media/File:Sine_cosine_one_period.svg
当我们将这个三角形和单位圆联系在一起的时候,sin(cos) 的几何意义就很明显了:
"Sine cosine one period" by Geek3 - Own work.
Licensed under CC BY 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Sine_cosine_one_period.svg#/media/File:Sine_cosine_one_period.svg
当我们将这个三角形和单位圆联系在一起的时候,sin(cos) 的几何意义就很明显了:
 "Circle-trig6" by This is a vector graphic version of Image:Circle-trig6.png by user:Tttrung which was licensed under the GFDL. Based on en:Image:Circle-trig6.png, which was donated to Wikipedia under GFDL by Steven G. Johnson. - This is a vector graphic version
of Image:Circle-trig6.png by user:Tttrung which was licensed under the GFDL. ; Based on en:Image:Circle-trig6.png, which was donated to Wikipedia under GFDL by Steven G. Johnson.. Licensed under CC BY-SA 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Circle-trig6.svg#/media/File:Circle-trig6.svg
图中红 {MOD}的线段长度就是 sin 的值,蓝 {MOD}的线段长度就是 cos 的值,如果我们假设坐标系的原点和单位圆重合,脑补一下下面的场景:有个小球(只能)沿着单位圆的圆周做运动。这时候,我们就会发现一个事实:
sin(t) 是小球 t 时刻在 y 轴上的投影,cos(t) 是小球 t 时刻在 x 轴上的投影。
进一步,当小球的运动速率是匀速率的时候,就有了上面提到的波形,更加形象的图如下:
"Circle-trig6" by This is a vector graphic version of Image:Circle-trig6.png by user:Tttrung which was licensed under the GFDL. Based on en:Image:Circle-trig6.png, which was donated to Wikipedia under GFDL by Steven G. Johnson. - This is a vector graphic version
of Image:Circle-trig6.png by user:Tttrung which was licensed under the GFDL. ; Based on en:Image:Circle-trig6.png, which was donated to Wikipedia under GFDL by Steven G. Johnson.. Licensed under CC BY-SA 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Circle-trig6.svg#/media/File:Circle-trig6.svg
图中红 {MOD}的线段长度就是 sin 的值,蓝 {MOD}的线段长度就是 cos 的值,如果我们假设坐标系的原点和单位圆重合,脑补一下下面的场景:有个小球(只能)沿着单位圆的圆周做运动。这时候,我们就会发现一个事实:
sin(t) 是小球 t 时刻在 y 轴上的投影,cos(t) 是小球 t 时刻在 x 轴上的投影。
进一步,当小球的运动速率是匀速率的时候,就有了上面提到的波形,更加形象的图如下:
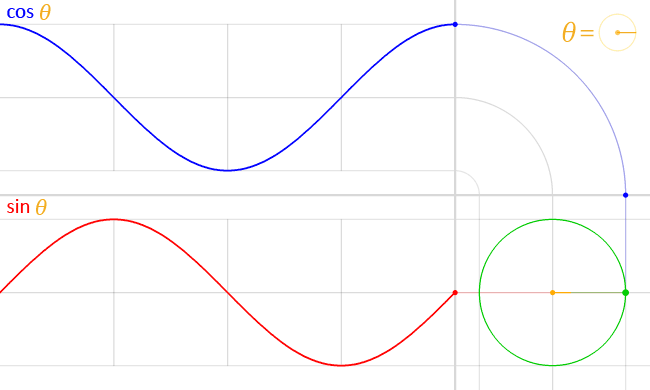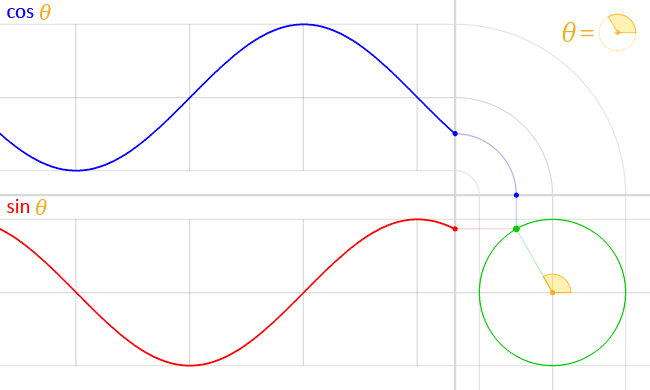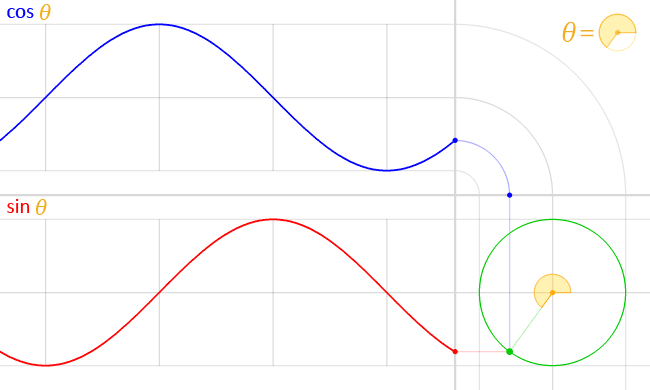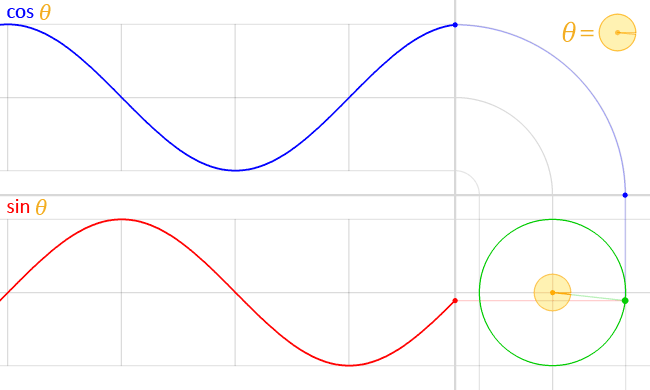 "Circle cos sin" by LucasVB - Own work. Licensed under Public Domain via Commons - https://commons.wikimedia.org/wiki/File:Circle_cos_sin.gif#/media/File:Circle_cos_sin.gif
P.S. 关于投影,wiki 上有个解释欧拉公式的图特别好:
"Sine and Cosine fundamental relationship to Circle (and Helix)" by Tdadamemd - Own work by uploader (.gif frames created in Powerpoint). Licensed under CC BY-SA 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Sine_and_Cosine_fundamental_relationship_to_Circle_(and_Helix).gif#/media/File:Sine_and_Cosine_fundamental_relationship_to_Circle_(and_Helix).gif
"Circle cos sin" by LucasVB - Own work. Licensed under Public Domain via Commons - https://commons.wikimedia.org/wiki/File:Circle_cos_sin.gif#/media/File:Circle_cos_sin.gif
P.S. 关于投影,wiki 上有个解释欧拉公式的图特别好:
"Sine and Cosine fundamental relationship to Circle (and Helix)" by Tdadamemd - Own work by uploader (.gif frames created in Powerpoint). Licensed under CC BY-SA 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Sine_and_Cosine_fundamental_relationship_to_Circle_(and_Helix).gif#/media/File:Sine_and_Cosine_fundamental_relationship_to_Circle_(and_Helix).gif
有了上面简单的背景,就可以开始逐个讨论信号处理中的概念了。
我们已经知道小球在圆周上做匀速率的圆周运动时,它在两个坐标轴上的投影就分别是 sin(cos),如果我们想进一步描述小球的运动速率的快慢呢? 假设小球完整转一圈所花费的时间为 T,转动的角度为 2π,则我们可以定义 模拟角频率
小球在二维平面上的圆周运动投影到一维的坐标轴 x(y) 轴上看,则是左右(上下)振动。和 Ω 类似,我们也可以定义一个物理量来描述这种振动的快慢: 小球完成一次完整的圆周运动所花费的时间为 T,也就是完成一次振动花费了 T 时间,我们定义 频率
计算机的世界是离散的,所以当连续信号经过采样、量化得到离散信号后: y = sin(Ωt) = sin(ΩnTs) = sin(ΩTsn) = sin(wn) 从数学上我们就可以得到: 数字角频率Item
Min
Mid
Max
n
0
(N-1)/2
N
Ω
0
Ωs/2
Ωs
f
0
Fs/2
Fs
w
0
π
2*π
由频谱的搬移过程可以知道,w 从 π 到 2π 是负频率搬移的结果,所以通常分析的时候 w 的范围为 [-π, π),如下
Item
Min
Mid
Max
Ω
-Ωs/2
0
Ωs/2
f
-Fs/2
0
Fs/2
w
-π
0
π
最近实习的时候,发现自己的 DSP 基本功还是不够扎实,关于模拟/数字角频率,频率,采样速率等一些概念理解的都不太深刻,愧对老师和这么多年的学习,Google 到一些讲解的比较清楚的 blog,备忘(抄袭)过来,温故而知新。
unit circle & sin(cos)
首先从最基本的三角函数的定义开始: 三角函数的定义方式有很多种,我觉得基于单位圆的定义是最形象,对之后理解各种角频率的物理/数学含义最有帮助。 我们应该是在初中的时候第一次接触到三角函数,那时候三角函数的定义是直接给个三角形,然后直接定义 sin(cos) 为哪条边比哪条边的值,然后给出 sin(cos) 的波形如下图所示:
 "Sine cosine one period" by Geek3 - Own work.
Licensed under CC BY 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Sine_cosine_one_period.svg#/media/File:Sine_cosine_one_period.svg
当我们将这个三角形和单位圆联系在一起的时候,sin(cos) 的几何意义就很明显了:
"Sine cosine one period" by Geek3 - Own work.
Licensed under CC BY 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Sine_cosine_one_period.svg#/media/File:Sine_cosine_one_period.svg
当我们将这个三角形和单位圆联系在一起的时候,sin(cos) 的几何意义就很明显了:
 "Circle-trig6" by This is a vector graphic version of Image:Circle-trig6.png by user:Tttrung which was licensed under the GFDL. Based on en:Image:Circle-trig6.png, which was donated to Wikipedia under GFDL by Steven G. Johnson. - This is a vector graphic version
of Image:Circle-trig6.png by user:Tttrung which was licensed under the GFDL. ; Based on en:Image:Circle-trig6.png, which was donated to Wikipedia under GFDL by Steven G. Johnson.. Licensed under CC BY-SA 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Circle-trig6.svg#/media/File:Circle-trig6.svg
图中红 {MOD}的线段长度就是 sin 的值,蓝 {MOD}的线段长度就是 cos 的值,如果我们假设坐标系的原点和单位圆重合,脑补一下下面的场景:有个小球(只能)沿着单位圆的圆周做运动。这时候,我们就会发现一个事实:
sin(t) 是小球 t 时刻在 y 轴上的投影,cos(t) 是小球 t 时刻在 x 轴上的投影。
进一步,当小球的运动速率是匀速率的时候,就有了上面提到的波形,更加形象的图如下:
"Circle-trig6" by This is a vector graphic version of Image:Circle-trig6.png by user:Tttrung which was licensed under the GFDL. Based on en:Image:Circle-trig6.png, which was donated to Wikipedia under GFDL by Steven G. Johnson. - This is a vector graphic version
of Image:Circle-trig6.png by user:Tttrung which was licensed under the GFDL. ; Based on en:Image:Circle-trig6.png, which was donated to Wikipedia under GFDL by Steven G. Johnson.. Licensed under CC BY-SA 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Circle-trig6.svg#/media/File:Circle-trig6.svg
图中红 {MOD}的线段长度就是 sin 的值,蓝 {MOD}的线段长度就是 cos 的值,如果我们假设坐标系的原点和单位圆重合,脑补一下下面的场景:有个小球(只能)沿着单位圆的圆周做运动。这时候,我们就会发现一个事实:
sin(t) 是小球 t 时刻在 y 轴上的投影,cos(t) 是小球 t 时刻在 x 轴上的投影。
进一步,当小球的运动速率是匀速率的时候,就有了上面提到的波形,更加形象的图如下:
 "Circle cos sin" by LucasVB - Own work. Licensed under Public Domain via Commons - https://commons.wikimedia.org/wiki/File:Circle_cos_sin.gif#/media/File:Circle_cos_sin.gif
P.S. 关于投影,wiki 上有个解释欧拉公式的图特别好:
"Sine and Cosine fundamental relationship to Circle (and Helix)" by Tdadamemd - Own work by uploader (.gif frames created in Powerpoint). Licensed under CC BY-SA 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Sine_and_Cosine_fundamental_relationship_to_Circle_(and_Helix).gif#/media/File:Sine_and_Cosine_fundamental_relationship_to_Circle_(and_Helix).gif
"Circle cos sin" by LucasVB - Own work. Licensed under Public Domain via Commons - https://commons.wikimedia.org/wiki/File:Circle_cos_sin.gif#/media/File:Circle_cos_sin.gif
P.S. 关于投影,wiki 上有个解释欧拉公式的图特别好:
"Sine and Cosine fundamental relationship to Circle (and Helix)" by Tdadamemd - Own work by uploader (.gif frames created in Powerpoint). Licensed under CC BY-SA 3.0 via Commons - https://commons.wikimedia.org/wiki/File:Sine_and_Cosine_fundamental_relationship_to_Circle_(and_Helix).gif#/media/File:Sine_and_Cosine_fundamental_relationship_to_Circle_(and_Helix).gif
有了上面简单的背景,就可以开始逐个讨论信号处理中的概念了。
Ω
我们已经知道小球在圆周上做匀速率的圆周运动时,它在两个坐标轴上的投影就分别是 sin(cos),如果我们想进一步描述小球的运动速率的快慢呢? 假设小球完整转一圈所花费的时间为 T,转动的角度为 2π,则我们可以定义 模拟角频率
Ω = 2π/T,单位是 rad / s
来描述小球的转动速率的快慢。
当 t = 2π 时,y = sin(Ω*2π),这时候可以看出 Ω 的物理含义:在 2π 的时间内,小球所完成的圈数。
下面的 Matlab 小程序演示了 2π 时间内 Ω 和周期的对应关系:
1
2
3
4
5
6
7
8
t = 0: pi/50: 2*pi;
for OMEGA = 1:4
y(:,OMEGA) = sin(OMEGA*t);
str{OMEGA} = ['OMEGA=', num2str(OMEGA)];
end
h = plot(t, y); grid on;
xlabel('t / s'); ylabel('amp'); title('y = sin(OMEGA*t)');
legend(h, str);
结果如下图:

f
小球在二维平面上的圆周运动投影到一维的坐标轴 x(y) 轴上看,则是左右(上下)振动。和 Ω 类似,我们也可以定义一个物理量来描述这种振动的快慢: 小球完成一次完整的圆周运动所花费的时间为 T,也就是完成一次振动花费了 T 时间,我们定义 频率
f = 1 / T,单位是 Hz
来描述振动的快慢。由前面 Ω 的定义式可知,Ω = 2π * f,有 y = sin(2π * f * t)。
当 t = 1s 时,y = sin(2π * f),这时候可以看出 f 的物理意义:在 1s 的时间内,小球所完成的振动次数。
下面的 Matlab 小程序演示了 1s 时间内 f 和振动周期的对应关系:
1
2
3
4
5
6
7
8
t = 0: 1/100: 1;
for f = 1:4
y(:,f) = sin(2*pi*f*t);
str{f} = ['f=', num2str(f)];
end
h = plot(t,y); grid on;
xlabel('t / s'); ylabel('amp'); title('y = sin(2*pi*f*t)');
legend(h, str);
结果如下图:

w
计算机的世界是离散的,所以当连续信号经过采样、量化得到离散信号后: y = sin(Ωt) = sin(ΩnTs) = sin(ΩTsn) = sin(wn) 从数学上我们就可以得到: 数字角频率
w = Ω*Ts = Ω / Fs,单位是 rad
可以看到,w 是用采样频率 Fs 对 Ω 进行归一化得到的,所以 w 准确地应该叫做归一化数字角频率。
连接模拟和数字的桥梁就是采样频率 Fs,由计算过程可以知道,w 相同的两个信号,它们的 Ω 不一定相同。因为丢失了 Fs 信息,所以单独讨论 w 是没有意义的。
虽然单独讨论 w 是没有意义的,但是这不代表 w 没有物理意义,当小球的振动频率为 f 时,每秒在圆周上转过的角度为 Ω = 2π * f,而采样频率为 Fs 就是说每秒钟对小球进行 Fs 次采样(拍照),显然有 Fs 个样值(照片)。这些样值(照片)是均匀分布的,所以每两个样值点之间的弧度为 2π * f / Fs = w,这也就是 w 的物理含义:相邻两个样值点之间的弧度数。
================================== summary ====================================
这几个频率之间是线性关系,可以得到下面的对应关系: