一、实验目的

(1)进一步了解离散时间序列时域的基本运算。 (2)通过实验进一步理解卷积定理，了解卷积的过程。 (3)了解MATLAB语言进行离散序列运算的常用函数，掌握离散序列运算程序的编写方法。

二、实验涉及的MATLAB子函数

1.find
功能：寻找非零元素的索引号。 调用格式：find((n>＝min(n1))&(n<＝max(n1)))；在符合关系运算条件的范围内寻找非零元素的索引号。 2.fliplr
功能：对矩阵行元素进行左右翻转。 调用格式：x1＝fliplr(x)；将x的行元素进行左右翻转，赋给变量x1。 3.conv
功能：进行两个序列间的卷积运算。 调用格式：y＝conv(x，h)；用于求取两个有限长序列x和h的卷积，y的长度取x、h长度之和减1。 例如，x(n)和h(n)的长度分别为M和N，则y＝conv(x，h)，y的长度为N＋M－1。 使用注意事项：conv默认两个信号的时间序列从n＝0开始，因此默认y对应的时间序号也从n＝0开始。 4.sum 功能：求各元素之和。 调用格式：Z＝sum(x)；求各元素之和，常用于等宽数组求定积分 5.hold 功能：控制当前图形是否刷新的双向切换开关。 调用格式：
holdon；使当前轴及图形保持而不被刷新，准备接受此后将绘制的新曲线。 holdoff；使当前轴及图形不再具备不被刷新的性质。 6.pause
功能：暂停执行文件。 调用格式：
pause；暂停执行文件，等待用户按任意键继续。 pause(n)；在继续执行之前，暂停n秒。 三、实验原理 离散序列的时域运算包括信号的相加、相乘，信号的时域变换包括信号的移位、反折、倒相及信号的尺度变换等。 在MATLAB中，离散序列的相加、相乘等运算是两个向量之间的运算，因此参加运算的两个序列向量必须具有相同的维数，否则应进行相应的处理。 下面用实例介绍各种离散序列的时域运算和时域变换的性质。 1.序列移位
将一个离散信号序列进行移位，形成新的序列：x1(n)＝x(n－m) 当m>0时，原序列x(n)向右移m位，形成的新序列称为x(n)的延时序列； 当m<0时，原序列x(n)向左移m位，形成的新序列称为x(n)的超前序列。 实例：
代码： %绘制u(n)、u(n+4)、u(n-4) n1=-5;n2=5; n=n1:n2; x= n>=0;%于n0处产生冲激 subplot(3,1,1),stem(n,x,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([n1,n2,0,1.1*max(x)]) %确定横坐标和纵坐标的取值范围 title('u(n)') xlabel('时间(n)'); ylabel('幅度x(n)'); x1= n>=-4; subplot(3,1,2),stem(n,x1,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([n1,n2,0,1.1*max(x)]) %确定横坐标和纵坐标的取值范围 title('u(n+4)') xlabel('时间(n)'); ylabel('幅度x(n)'); x2=n>=4; subplot(3,1,3),stem(n,x2,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([n1,n2,0,1.1*max(x)]) %确定横坐标和纵坐标的取值范围 title('u(n-4)') xlabel('时间(n)'); ylabel('幅度x(n)'); 输出：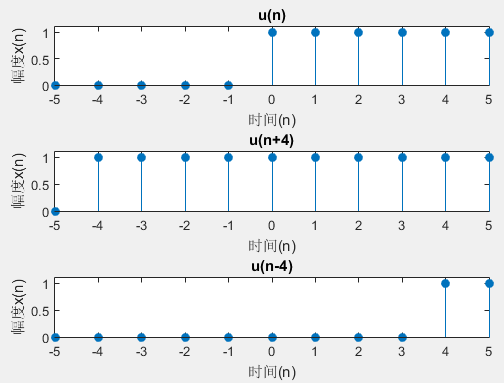
2.序列相加
两个离散序列相加是指两个序列中相同序号n(或同一时刻)的序列值逐项对应相加，构成一个新的序列：
情况1： 参加运算的两个序列具有相同的维数。 实例，求 (0< n <10) 代码： n1=-5;n2=5; n=n1:n2; x= n==2;%于n0处产生冲激 subplot(3,1,1),stem(n,x,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([n1,n2,0,1.1*max(x)]) %确定横坐标和纵坐标的取值范围 title('u(n)') xlabel('时间(n)'); ylabel('幅度x(n)'); x1= n==4; subplot(3,1,2),stem(n,x1,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([n1,n2,0,1.1*max(x)]) %确定横坐标和纵坐标的取值范围 title('u(n+4)') xlabel('时间(n)'); ylabel('幅度x(n)'); x2= n==4|n==2; subplot(3,1,3),stem(n,x2,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([n1,n2,0,1.1*max(x)]) %确定横坐标和纵坐标的取值范围 title('u(n-4)') xlabel('时间(n)'); ylabel('幅度x(n)'); 输出：
情况2：参加运算的两个序列的维数不同。
实例，已知，求 代码： n1=-3:5;k1=-2; n2=-4:7;k2=4; x1= n1-k1>=0;%x1信号 x2= n2-k2>=0;%x2信号 n=min([n1,n2]):max([n1,n2]); N=length(n); y1=zeros(1,N); y2=zeros(1,N); y1(find(n>=min(n1)&n<=max(n1)))=x1; y2(find(n>=min(n2)&n<=max(n2)))=x2; y=y1+y2; min_n=min(n); max_n=max(n); min_y=min(y); max_y=max(y); subplot(3,1,1),stem(n1,x1,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([min_n,max_n,min_y,1.1*max_y]) %确定横坐标和纵坐标的取值范围 title('u(n+2)(-4) subplot(3,1,2),stem(n2,x2,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([min_n,max_n,min_y,1.1*max_y]) %确定横坐标和纵坐标的取值范围 title('u(n+4)(-5) subplot(3,1,3),stem(n,y1+y2,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([min_n,max_n,min_y,1.1*max_y]) %确定横坐标和纵坐标的取值范围 title('信号叠加') 输出：
3.序列相乘 两个离散序列相乘是指两个序列中相同序号n(或同一时刻)的序列值逐项对应相乘，构成一个新的序列x(n)＝x1(n)×x2(n)，这里同样存在着序列维数相同和不同两种情况，处理方法与序列相加相同。 实例，已知，求 x(n)＝x1(n)×x2(n) 代码： n1=-3:5;k1=-2; n2=-4:7;k2=4; x1= n1-k1>=0;%x1信号 x2= n2-k2>=0;%x2信号 n=min([n1,n2]):max([n1,n2]); N=length(n); y1=zeros(1,N); y2=zeros(1,N); y1(find(n>=min(n1)&n<=max(n1)))=x1; y2(find(n>=min(n2)&n<=max(n2)))=x2; y=y1.*y2; min_n=min(n); max_n=max(n); min_y=min(y); max_y=max(y); subplot(3,1,1),stem(n1,x1,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([min_n,max_n,min_y,1.1*max_y]) %确定横坐标和纵坐标的取值范围 title('u(n+2)(-4) subplot(3,1,2),stem(n2,x2,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([min_n,max_n,min_y,1.1*max_y]) %确定横坐标和纵坐标的取值范围 title('u(n+4)(-5) subplot(3,1,3),stem(n,y,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([min_n,max_n,min_y,1.1*max_y]) %确定横坐标和纵坐标的取值范围 title('信号相乘') 输出： 4.序列反折
离散序列反折是指离散序列的两个向量以零时刻的取值为基准点，以纵轴为对称轴反折。在MATLAB中提供了fliplr函数，可以实现序列的反折。 实例：已知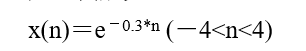，　求它的反折序列x(－n)。 代码： n=-3:3; x=exp(-0.3*n); x1=fliplr(x); subplot(2,1,1),stem(n,x,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([-4,4,min(x),1.1*max(x)]) %确定横坐标和纵坐标的取值范围 subplot(2,1,2),stem(n,x1,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([-4,4,min(x),1.1*max(x)]) %确定横坐标和纵坐标的取值范围 输出：
5.序列倒相 离散序列倒相是求一个与原序列的向量值相反，对应的时间序号向量不变的新的序列。 实例：给定，　求-x(n)。
代码： n=-3:3; x=exp(-0.3*n); x1=-1*x; subplot(2,1,1),stem(n,x,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([-4,4,min(x),1.1*max(x)]) %确定横坐标和纵坐标的取值范围 subplot(2,1,2),stem(n,x1,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 axis([-4,4,1.1*min(x1),max(x1)]) %确定横坐标和纵坐标的取值范围 输出：
6.序列的尺度变换
对于给定的离散序列x(n)，序列x(mn)是x(n)每隔m点取一点形成，相当于时间轴n压缩了m倍；
反之，序列x(n/m)是x(n)作m倍的插值而形成的，相当于时间轴n扩展了m倍。 实例： 已知信号x(n)＝sin(2* pi *n)，求x(2n)和x(n/2)的信号波形。为研究问题的方便，取0<=n<=20，并将n缩小20倍进行波形显示。 代码： n=(0:20)/20;%记得除以20，将n缩小20倍后比较容易观察出区别 x=sin(2*pi*n); x1=sin(2*pi*2*n); x2=sin(2*pi*n/2); subplot(3,1,1),stem(n,x,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 title('x(n)') subplot(3,1,2),stem(n,x1,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 title('x(2n)') subplot(3,1,3),stem(n,x2,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 title('x(n/2)') 输出：
7.直接使用conv进行卷积运算
求解两个序列的卷积，很重要的问题在于卷积结果的时宽区间如何确定。在MATLAB中，卷积子函数conv默认两个信号的时间序列从n＝0开始，y对应的时间序号也从n＝0开始。 已知两个信号序列：　f1＝0.8^n (0<=n<=20)、f2＝u(n) (0<=n<=10),求两个序列的卷积和。 代码： n1=0:20; f1=0.8.^n1; n2=0:10; f2= ones(1,length(n2));%若是使用 f2= n2>=0的话，conv函数会报错 f3=conv(f1,f2); subplot(3,1,1),stem(n1,f1,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 title('f1') subplot(3,1,2),stem(n2,f2,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 title('f2') subplot(3,1,3),stem(f3,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 title('f1卷积f2') 输出：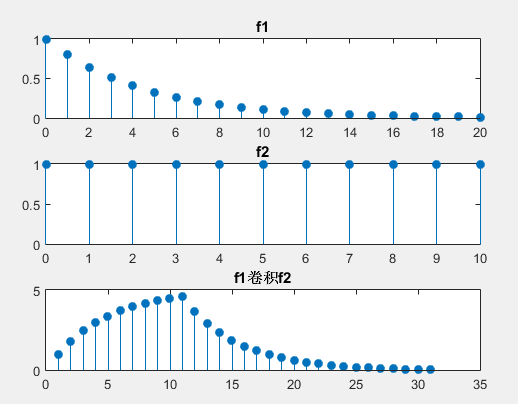

很奇怪，如果f2是logical类型conv函数就会报错。比如改成：f2=double(n2>=0);也bu不会报错。 8.复杂序列的卷积运算
由于MATLAB中卷积子函数conv默认两个信号的时间序列从n＝0开始，因此，如果信号不是从0开始，则编程时必须用两个数组确定一个信号，其中，一个数组是信号波形的幅度样值，另一个数组是其对应的时间向量。此时，程序的编写较为复杂，我们可以将其处理过程编写成一个可调用的通用子函数，如下。 %convnew.m function [y,ny]= convnew(x,nx,h,nh)%建立convnew子函数 %x为一信号幅度样值向量，nx为x对应的时间向量 %h为另一信号或系统冲激函数的非零样值向量，nh为h对应的时间向量 %y为卷积积分的非零样值向量，ny为其对应的时间向量 n1=nx(1)+nh(1); %计算y的非零样值的起点位置 n2=nx(length(x))+nh(length(h));%计算y的非零样值的宽度 ny=n1:n2; %确定y的非零样值时间向量 y=conv(x,h); 实例：给定两个信号序列：f1为0.5n(0 < n <10)的斜变信号序列；f2为一个u(n＋2)(－2 < n < 10)的阶跃序列，求两个序列的卷积和。 思考： 从信号序列n的范围可见，f2的时间轴起点不是n＝0，因此，该程序需使用卷积子函数convnew进行计算。 代码： n1=0:10; f1=0.5*n1; n2=-2:10; f2=ones(1,length(n2));%若是使用 f2= n2>=0的话，conv函数会报错 [f3,n3]=convnew(f1,n1,f2,n2); subplot(2,2,1),stem(n1,f1,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 title('f1') subplot(2,2,2),stem(n2,f2,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 title('f2') subplot(2,1,2),stem(n3,f3,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 title('f1卷积f2') 输出：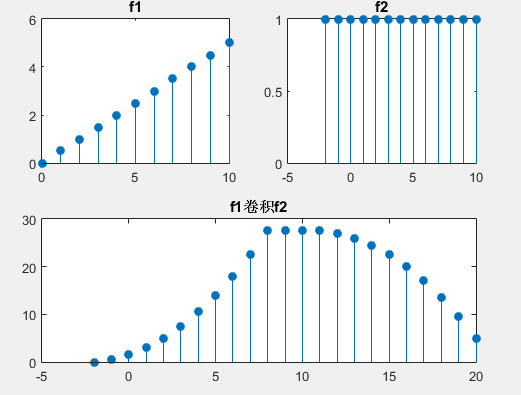
看到这里，如果是有详细操作过这个例子的话，可能会说“我用conv得到的结果也是这样的呀”。其实不然。若是用conv，那么其代码是这样写的： n1=0:10; f1=0.5*n1; n2=-2:10; f2=ones(1,length(n2));%若是使用 f2= n2>=0的话，conv函数会报错 %---------不同之处1---------start f3=conv(f1,f2); %---------不同之处1---------end subplot(2,2,1),stem(n1,f1,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 title('f1') subplot(2,2,2),stem(n2,f2,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 title('f2') %---------不同之处2---------start subplot(2,1,2),stem(f3,'filled');%绘制脉冲杆图，且圆点处用实心圆表示 %---------不同之处2---------end title('f1卷积f2') 输出为：
仔细和上面的例子相比，还是有区别的，比如n=20时，后者的结果明显比前者的大。 9.卷积积分的动态过程演示
为了更深入地理解两个序列卷积的原理，下面提供一段演示卷积积分的动态过程的MATLAB程序。 动态地演示 求解信号序列f1＝0.8n (0 < n < 20)和f2＝u(n) (0 < n < 10)卷积和的过程。 clf; %图形窗清屏 nf1=0:20; %建立f1的时间向量 f1=0.8.^nf1; %建立f1序列 lf1=length(f1);%取f1时间向量的长度 nf2=0:10; %f2的时间向量 lf2=length(nf2);%取f2时间向量的长度 f2=ones(1,lf2);%建立f2序列 lmax=max(lf2,lf1);%求最长的序列 if lf2>lf1 nf2=0;nf1=lf2-lf1;%若f2比f1长,对f1补nf1个0 elseif lf20;nf2=lf1-lf2;%若f1比f2长,对f2补nf2个0 else nf2=0;lf1=0; %若f1与f2同长,不补0 end lt=lmax; %取长者为补0长度基础 %先将f2补得与f1同长,再将两边补最大长度的0 u=[zeros(1,lt),f2,zeros(1,nf2),zeros(1,lt)]; t1=(-lt+1:2*lt);%先将f1补得与f2同长,再将左边补2倍最大长度的0 f1=[zeros(1,2*lt),f1,zeros(1,nf1)]; hf1=fliplr(f1); %将f1作左右反折 N=length(hf1); y=zeros(1,3*lt); %将y存储单元初始化 for k=0:2*lt %动态演示绘图 p=[zeros(1,k),hf1(1:N-k)];%使hf1向右循环移位 y1=u.*p; %使输入和翻转移位的脉冲过渡函数逐项相乘 yk=sum(y1); %相加 y(k+lt+1)=yk;%将结果放入数组y subplot(4,1,1);stem(t1,u); subplot(4,1,2);stem(t1,p); subplot(4,1,3);stem(t1,y1); subplot(4,1,4);stem(k,yk);%作图表示每一次卷积的结果 axis([-20,50,0,5]); hold on %在图形窗上保留每一次运行的图形结果 pause(1); %停顿1秒钟 end 修改代码，将动态过程保存为gif动图： clf; %图形窗清屏 nf1=0:20; %建立f1的时间向量 f1=0.8.^nf1; %建立f1序列 lf1=length(f1);%取f1时间向量的长度 nf2=0:10; %f2的时间向量 lf2=length(nf2);%取f2时间向量的长度 f2=ones(1,lf2);%建立f2序列 lmax=max(lf2,lf1);%求最长的序列 if lf2>lf1 nf2=0;nf1=lf2-lf1;%若f2比f1长,对f1补nf1个0 elseif lf20;nf2=lf1-lf2;%若f1比f2长,对f2补nf2个0 else nf2=0;lf1=0; %若f1与f2同长,不补0 end lt=lmax; %取长者为补0长度基础 %先将f2补得与f1同长,再将两边补最大长度的0 u=[zeros(1,lt),f2,zeros(1,nf2),zeros(1,lt)]; t1=(-lt+1:2*lt);%先将f1补得与f2同长,再将左边补2倍最大长度的0 f1=[zeros(1,2*lt),f1,zeros(1,nf1)]; hf1=fliplr(f1); %将f1作左右反折 N=length(hf1); y=zeros(1,3*lt); %将y存储单元初始化 for k=0:2*lt %动态演示绘图 p=[zeros(1,k),hf1(1:N-k)];%使hf1向右循环移位 y1=u.*p; %使输入和翻转移位的脉冲过渡函数逐项相乘 y(k+lt+1)=yk;%将结果放入数组y subplot(4,1,1);stem(t1,u); subplot(4,1,2);stem(t1,p); subplot(4,1,3);stem(t1,y1); subplot(4,1,4);stem(k,yk);%作图表示每一次卷积的结果 axis([-20,50,0,5]); hold on %在图形窗上保留每一次运行的图形结果 pause(1); %停顿1秒钟 %---------------------创建gif------------------------------- Filename='dynamicconv.gif';%文件名 f=getframe(gcf); imind=frame2im(f); [imind,cm] = rgb2ind(imind,256); if k==0 %起始值必须为0，对应循环中k的首个值 imwrite(imind,cm,Filename,'gif', 'Loopcount',inf ,'DelayTime', 1);%第一次必须创建！ else imwrite(imind,cm,Filename,'gif','WriteMode','append','DelayTime', 1); end %---------------------创建gif------------------------------- end 效果：