一直很想深入学习滤波器方面的知识,图书馆也去借了书然后准备看,结果就是:然后就没有然后了。DSP一直是自己的短板,因为这里面感觉小的技巧好多,而且都需要自己去琢磨,像滤波器这种东西,我脑海里也只有少的可怜点印象。比如什么FIR 和 IIR 之类的。理论尚且薄弱更不谈实践了,这也是制约自己进一步提高的重要方面。但是,现在的自己仿佛早已经没了以前那么耐心去啃书了,最多上网googling,再看点博文。所以,前今天看到导师改的msn签名:静心!觉得很有启发,确实啊现在这个急功近利的社会,要做到的确有难度。说到这,又不得不再次表达对杨鸿文老师的敬佩,我觉得他应该是真正做到了那点,现在是很难再找到这样热爱自己工作的老师了,除了敬佩只剩瞻仰! 貌似每次写正文前,我都要唠叨几句。哎,唠叨唠叨也就过去了,人一辈子也不就这样嘛。好了,言归正传,今天谈谈最常见的滤波器—-升余弦滤波器。先说说我们为什么这么喜欢这个滤波器,最主要的原因就是它的拖尾衰减的比Nyquist滤波器(sinc())快,这样的好处就是当我们出现了定时误差的时候,码间干扰尽可能降低了。另一方面,既然衰减快了,说明它的频率成分肯定是增加了,这就导致带宽的增加。所以,它是以带宽换取低ISI的典型应用。接下来给出升余弦滤波器时域和频域表达式:
 接下来我们就实践下,我们从时域来产生滤波器,再验证频域图像是否正确。
接下来我们就实践下,我们从时域来产生滤波器,再验证频域图像是否正确。
- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- % Author : ZXY
- % Email : zxy_ee@163.com
- % Version : 1.0
- % Date : 2012-2-16
- % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- 看代码,直接点左上角view plain!
- clear all
- fs = 20;
- %we define T = 1,so we ignore it!!
- % defining the sinc filter
- sincNum = sin(pi*[-fs:1/fs:fs]); % numerator of the sinc function
- sincDen = (pi*[-fs:1/fs:fs]); % denominator of the sinc function
- sincDenZero = find(abs(sincDen) < eps);%the eps is 2.2204e-016
- sincOp = sincNum./sincDen;
- sincOp(sincDenZero) = 1; % sin(pix/(pix) =1 for x =0 诺比达法则
- alpha = 0;
- cosNum = cos(alpha*pi*[-fs:1/fs:fs]);
- cosDen = (1-(2*alpha*[-fs:1/fs:fs]).^2);
- cosDenZero = find(abs(cosDen)<eps);
- cosOp = cosNum./cosDen;
- cosOp(cosDenZero) = pi/4;
- gt_alpha0 = sincOp.*cosOp;
- N = length(gt_alpha0);
- GF_alpha0 = fft(gt_alpha0,N);
- alpha = 0.5;
- cosNum = cos(alpha*pi*[-fs:1/fs:fs]);
- cosDen = (1-(2*alpha*[-fs:1/fs:fs]).^2);
- cosDenZero = find(abs(cosDen)<eps);
- cosOp = cosNum./cosDen;
- cosOp(cosDenZero) = pi/4;%诺比达法则直接计算
- gt_alpha5 = sincOp.*cosOp;
- N = length(gt_alpha5);
- GF_alpha5 = fft(gt_alpha5,N);
- alpha = 1;
- cosNum = cos(alpha*pi*[-fs:1/fs:fs]);
- cosDen = (1-(2*alpha*[-fs:1/fs:fs]).^2);
- cosDenZero = find(abs(cosDen)<eps);
- cosOp = cosNum./cosDen;
- cosOp(cosDenZero) = pi/4;
- gt_alpha1 = sincOp.*cosOp;
- N = length(gt_alpha5);
- GF_alpha1 = fft(gt_alpha1,N);
- close all
- figure
- plot([-fs:1/fs:fs],[gt_alpha0],'r','LineWidth',2)
- hold on
- plot([-fs:1/fs:fs],[gt_alpha5],'g','LineWidth',2)
- plot([-fs:1/fs:fs],[gt_alpha1],'b','LineWidth',2)
- legend('alpha=0','alpha=0.5','alpha=1');
- grid on
- xlabel('时间, t')
- ylabel('幅度, g(t)')
- title('时域图像')
- figure
- %除以fs的原因是因为采样导致幅度加权了。
- plot([-N/2:N/2-1]/N*fs, abs(fftshift(GF_alpha0))/fs,'r','LineWidth',2);
- hold on
- plot([-N/2:N/2-1]/N*fs, abs(fftshift(GF_alpha5))/fs,'g','LineWidth',2);
- plot([-N/2:N/2-1]/N*fs, abs(fftshift(GF_alpha1))/fs,'b','LineWidth',2);
- legend('alpha=0','alpha=0.5','alpha=1');
- axis([-2 2 0 1.2])
- grid on
- xlabel('频率, f')
- ylabel('幅值, |G(f)|')
- title('频域图像')
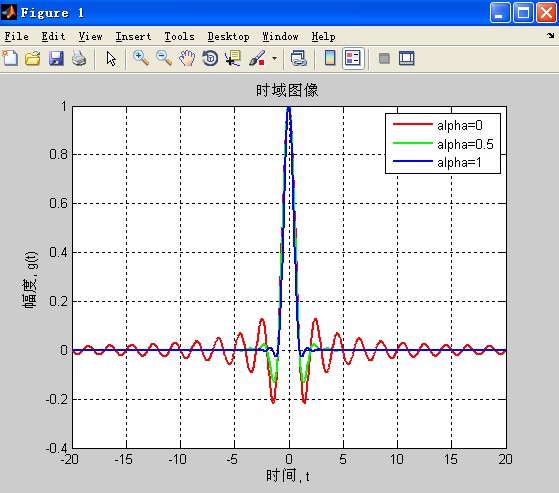
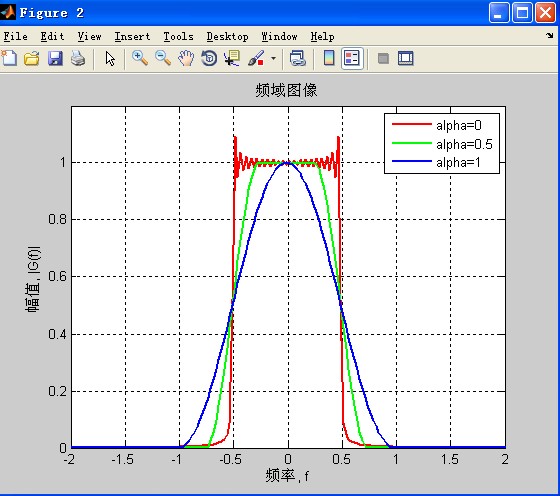 好了,我们可以看出与理论分析是一致的,由于我们用的是很粗暴的矩形窗,所以你能明显看见吉布斯现象。同样,当拖尾衰减更快时,它的频域也无情地展开了。这个仿真的难点还是写出它的时域表达式,其他的都还好说。原来仿真很少加窗,现在可以用上自己的升余弦了,不再去用自带的函数,参数不好记啊那些。关键是对原理更清楚了。比如:我们数据发送出去之前,要成形滤波,这样来抵抗ISI,那么我们就用数据与这里的滤波器(准确说是带根号,整体效果还是一个升余弦)做卷积运算。注意的是,这里的数据也要相应的过采样,关于采样,等自己弄明白来说,好多东西自己还没理解那么透彻。完!
本文转载自:https://blog.csdn.net/mike190267481/article/details/7264827
好了,我们可以看出与理论分析是一致的,由于我们用的是很粗暴的矩形窗,所以你能明显看见吉布斯现象。同样,当拖尾衰减更快时,它的频域也无情地展开了。这个仿真的难点还是写出它的时域表达式,其他的都还好说。原来仿真很少加窗,现在可以用上自己的升余弦了,不再去用自带的函数,参数不好记啊那些。关键是对原理更清楚了。比如:我们数据发送出去之前,要成形滤波,这样来抵抗ISI,那么我们就用数据与这里的滤波器(准确说是带根号,整体效果还是一个升余弦)做卷积运算。注意的是,这里的数据也要相应的过采样,关于采样,等自己弄明白来说,好多东西自己还没理解那么透彻。完!
本文转载自:https://blog.csdn.net/mike190267481/article/details/7264827