文章目录

• 信号处理与向量空间
• 向量表示信号
• 向量空间
• 向量的内积
• 基向量
• 基于子空间的近似估计
• 一个近似估计的例子：用多项式函数估计$sin t$
• 总结

信号处理与向量空间

向量表示信号

• 一个离散信号序列能够很自然的表示成向量：$x[n] = [x_0, x_1, cdots, x_{N-1}]^T$
• 为什么要用向量表示信号？因为更简单的数学表达和统一的信号处理框架
  1. 对不同类型的信号（四种：有限长、无限长、周期、有限支持）具有相同的处理框架
  2. 对连续信号具有相同的处理框架
  3. 更容易解释傅里叶变换
  4. 更容易解释采样与插值
  5. 在近似估计和压缩中非常有用
  6. 通讯系统设计中非常重要

向量空间

• 常见的向量空间。例如有$mathbb{R}^2$和$mathbb{R}^3$是二维和三维欧几里得空间
• $mathcal{l}_2(mathbb{Z})$：具有无限长度且平方可和的序列所构成的空间。例如矩形序列
• $L_2([a,b])$：在区间$[a,b]$上平方可积的函数所构成的空间（没错，向量可以是函数）。例如 ${x=sin(t), tin [-1, 1]}in L_2([-1,1])$，因为$sin(t)$在$[-1,1]$上平方可积
• 向量空间的基本性质和操作
  

向量的内积

• 内积是一个标量，内积用于衡量向量之间的相似度
• 两个向量的内积操作可以表示为：$<mathbf{x},mathbf{y}>=Vert mathbf{x}Vert Vert mathbf{y}Vert cos heta$，其中$heta$表示向量之间的夹角
• 如果两个向量的内积为0，那么它们正交（相似度为0，$heta=pi/2$）
• 向量内积的基本性质
  
• $L_2([-1,1])$的内积定义：$<mathbf{x},mathbf{y}> = int_{-1}^1x(t)y(t) mathbf{d}t$。下图是一个例子
  
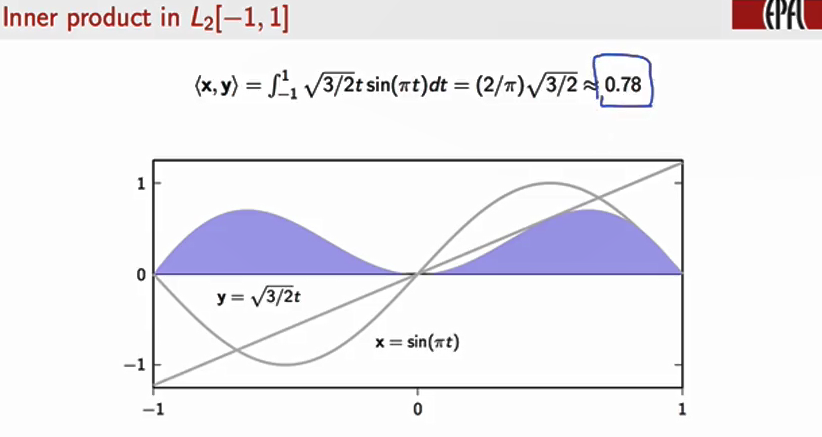
• 向量的长度用内积定义：$Vert xVert = sqrt{<mathbf{x},mathbf{x}> }$
• 向量之间的距离用内积定义：$mathbf{d}(mathbf{x},mathbf{y}) = Vert mathbf{x}-mathbf{y}Vert$。例如在二维空间中$Vert mathbf{x}-mathbf{y}Vert = sqrt{(x_0-y_0)^2 + (x_1-y_1)^2}$；在$L_2([-1,1])$上$Vert mathbf{x}-mathbf{y}Vert = int_{-1}^1vert x(t) - y(t) vert^2 mathbf{d}t$
• 一组信号可以表示成一个向量：$x[n] = [x_0, x_1, cdots, x_{N-1}]^T$，其中$x[n]$是一个复数，那么
  • 有限长度的信号的内积表示为：$<mathbf{x},mathbf{y}> = sum_{n=0}^{N-1}x^*[n]y[n]$，$*$表示共轭
  • 无限长度的信号的内积表示为：$<mathbf{x},mathbf{y}> = sum_{-infty}^{infty}x^*[n]y[n]$。其内积可能会无穷大，因此我们要求这个无限长度的信号属于$mathcal{l}_2(mathbb{Z})$空间，即要求$sum vert x[n]vert^2 < infty$

基向量

• 任意一个向量都通过线性组合基向量来得到。下图为二维空间的两个例子
  
  
• 基向量间要求线性无关，否则无法表示整个空间的向量
• 一组信号$x[n] = [x_0, x_1, cdots, x_{N-1}]^T$，可以看做一个N维的向量
• 一个无限长度的信号（向量）可以表示为：$mathbf{x}= sum_{k=0}^{infty} alpha_k w^{(k)}$，其中$alpha_k$为缩放系数，$w^{(k)}$为基向量。
• 函数向量空间：$f(t) = sum_k alpha_k h^{(k)}(t)$。其中