简单脉搏波波形分析系统设计与实现

@Author: J.Y.Liu @Date: 2012.03.22
转载自匆匆往站 https://blog.csdn.net/prog_6103/article/details/9121237 摘要 中医学是中国五千年文化的一块瑰宝。随着电子技术的发展，脉诊仪已民用化。为了探索脉诊仪得到的脉搏波数据所蕴含的信息，与脉诊仪相关的一系列定量数学模型将在文章中建立起来，包括脉搏波物理模型、病灶分析模型、中药与方剂模型。这些模型会被计算机程序一一实现，通过波形可视化，频谱计算，结合数据库技术，自动推荐出适用方剂，最终得到可以和特定脉诊仪配套使用的脉搏波波形分析系统。

Abstract
Traditional Chinese Medicine is a jade of Chinese culture in thousands of years. As electronic technique is developed, common people can use device for collecting pulse wave data easily. To discover deeply information in huge pulse wave data, a series of quantitative models related are established. They include physical pulse wave model, medical focus model and pharmacal model. They are implemented by a computer program, written in C#. The program is a pulse wave analysis system, which works with specified data that a pulse wave device collects. It gets features like pulse wave visualization, frequency spectrum histogram and an action to make a list of recommended prescriptions automatically with SQLite database technology.

目　　录

1.概述

1.1 中医面临的压力

1.2 西医新的起点

1.3 信息时代与中医

1.4 脉搏波与脉诊仪

2.硬件部分

2.1 脉诊仪测量原理

2.2 ARM平台与uClinux

3.数学第一部分：基础模型

3.1 血液波动模型

3.2 脉搏信号模型

4.软件第一部分：脉搏波处理

4.1 信号数据文件的分析

4.2 病灶分析算法

5.数学第二部分：中医信息模型

5.1 中药经验模型

5.2 方剂统计模型

6.软件第二部分：药物治疗分析

6.1 数据库构建

6.2 方剂推荐算法

7.结论
参考文献

1. 概述

1.1 中医面临的压力

中医是华夏民族千年文化的结晶。2006年国内再次掀起了一场中医存留的大讨论。为何会出现这么一场争论呢？首先中医的哲学基础没有被接受。其实马克思主义的辩证法早在中医的平衡哲学就有所体现了，马克思只是替这种体系取了个名字并牵引到政治经济领域。中医的哲学抽象性比较高，但这并不代表它就不能被大众接受。拒绝的原因不胜其数，翻阅文献，不难发现一些重要线索：中医的起源目前没有明确记载，所传承的文化直接告诉我们所有经络和基础知识；古代酷刑经常拆解人体，给古代人体解剖学提供了极大的方便。
中药的发展给人映像深刻，从《神农本草经》到《本草纲目》，再到目前的《中药大辞典》，药物逐渐增多，可以大概看出，中医的发展经过了定量的过程——像现代化学测定药物LD50、LE50等一样，中药也有过定量试验，使得很多方剂中都有中药用量的记载。我们可以大胆猜测，中医经历了西医的全部过程，从感性疾病的认识到定量准确的研究，然而随着时间的发展，经验足够应付所有疾病，导致人们逐渐抛弃定量研究，直接承接前人成果，最终形成知识断层。接着，地球环境的变迁，使得原有的经验开始产生误差，当中医的自我校正速率小于环境变化速率时，它开始变得不可靠，就是中医的压力了。于是大家这个时候就要怀疑中医的正确性了，这看上去是一种学科退化的过程，从中医哲学来说，是经验长期主导导致平衡转移的过程。所以我们现在要去使用定量研究去保持原有的平衡，正所谓拯救中医。

1.2 西医新的起点

西医按照中医可能原有的路线茁壮发展。在国人还在争论中医是否需要废止的同时，西方已经对中医理论进行了大量翻译。德国人以中医理论为基石，创立了能量医学，成为西医发展的一个新起点。加上生物学科的不断发展，技术不断成熟，能量医学正在试图达到中医原有的技术高度。中医基础理论的建设迫在眉睫，我们需要尽快理清中医的思路，这样才能让中医继续长久流传下去。

1.3 信息时代与中医

21世纪是信息时代。很多重复劳动都可以交给计算机完成。只要某项任务步骤简单，定量明确，就可以很好地利用计算机去自动解决。中医得到了发展的机遇，它拥有大量的临床经验，进入计算机，通过特定策略，便可以指导医师对病人进行治疗。同时它面临挑战，人工智能中数据挖掘技术尚未成熟，而偷懒的人们寄托于这项技术自动分析中医积累的经验，虽然会有一些成果，但这种优越感并不会长久。我们必须从最基础的理论开始，将中医离散的经验用数学知识进行压缩，形成连续的简单公式，然后再将它应用于计算机。

1.4 脉搏波与脉诊仪

美籍华人王维工教授在2006年出版了《气的乐章》一书，他从养生的角度，稍带学术地探讨了中医的基础理论。他便是能定位病灶的脉诊仪的设计人之一。人的心脏每时每刻都在跳动，这种跳动使血液在血管中波动循环。中医中手太阴肺经的列缺穴附近就能比较强烈的感觉到这种波动，古代医家大多数都是对这里进行脉诊测量的。

脉诊仪就是对脉搏波进行实时测量，并使用计算机对得到的数据进行自动分析，医生可以根据产生的结果对病人进行治疗。三部九候的脉诊方法得到的二十八脉象便是对脉搏波进行离散化分类，现代脉象的测量就是把古人脉诊的过程托管给机器操作。
后面我们将对脉诊仪的一整套体系展开调研。一方面通过使用Proteus等电路仿真软件，了解脉诊仪的硬件构造，探索其数据收集的原理；另一方面，为了让得到的数据更容易理解，我们还需要开发相应的软件对它们进行可视化，并能够自动分析得出数据供体的目前病理状态，再对这种状态通过打分的形式推荐一些相应的治疗方剂。

2. 硬件部分

2.1 脉诊仪测量原理

压力传感器是一种将压力转换为电信号输出的传感器。电阻性质和物质弹性是压力传感器的理论基础。
电阻计算公式为
R=ρ*l/S 现在有一个理想的长方形片状电阻，长a宽b，电流是沿着长的方向（不妨设为左右方向）流过。当给电阻上下施加压力的时候，由于弹性形变，使得其宽减小了△b，则电阻长度变为ab/(b-Δb)，因为△b大于0，所以变化后的电阻长度大于a，因为根据电阻计算公式R∝l，所以变化后的电阻阻值变大了。
由胡克弹性定理，有
F=-kΔb
其中k为电阻材质的弹性系数，则
Δb=-F/k
故电阻弹性形变后阻值为
R=ρ k/(kb+F)
在电阻两端加电压U，由欧姆定理
I=U/R
得
I=(U(kb+F))/ρk
所以在压力传感原理下的脉诊仪中，需要有一个能够弹性形变的电阻和一个电流计，压力传感器与电流放大电路相连，再加入电流计，我们只要记录电流计上的示数就可以得到脉搏波的波形数据了。

2.2 ARM平台与uClinux

嵌入式的技术正突飞猛进，ARM核已经十分普遍。目前小型脉诊仪还都需要与计算机进行交互，将传感器得到的数据送入电脑再进行处理。其实我们可以直接将脉诊的整个过程都集成在脉诊仪里，让它更加自动化，直接测量数据就能得出分析结果，并给出相应建议。

以上的设想，可以通过ARM核方便实现，因为Linux操作系统早已经被移植到了这一平台上。只要了解清楚ARM核的各项功能，配合开放源代码的uClinux，对数据处理和分析已经手到擒来。

3. 数学第一部分：基础模型

3.1 血液波动模型

首先，我们需要给出血液运动的基本模型，为硬件部分的实现提供可行性。众所周知，人体的血液是运行在血管内的。心脏在不停地向外泵血，它每跳动一次，都会喷射出一股血液，并以波的形式进行传播。而血管又是弹性的，所以在体表浅处如果有动脉血流经过，我们可以很容易通过触觉神经在其附近感觉到它的波动，它就是脉搏波了。伟大的祖先在几千年前就发现了这种存在。早在难经时就已经有了三部九候，到晋代王叔和在《脉经》中将脉象总结为二十四种，明代的李时珍将二十七种脉象的总结写在《濒湖脉学》里，后来李士材在《诊家正眼》中修订为二十八脉，就是现代脉象分类的雏形了。由此，我们便对脉象有了一个定性的认识。

为了对脉象进行数值测量，定性的知识是远远不够的，所以我们需要一个具体的数学模型去定量描述脉搏的跳动。目前，脉搏波的数学模型最成熟的要数弹性腔模型，而纯几何上我们可以使用三个高斯函数对脉搏波形进行拟合，而工程上则更注重实用性，所以工程师们发明了等效转换的方法，他们将血液循环系统等效成电子电路系统，然后通过计算电路的电阻、电感和电容来得到一组评估被测者身体状态的参数。深入浅出，这里我们只需要一个简单的公式说明人体血压存在，其实这并不复杂，高中的物理知识就能解决问题。以下，我们需要用到三个物理定理：
胡克弹性定理 F=-kx
F：弹性受力；k：弹性系数；x：弹性位移，即物体离平衡点的距离

力与压强关系定律 F=pS
F：压迫力；p：压强；S：受压物体与施压物体间的接触面积

流量与流速关系定律 Q=vA
Q：流体在单位时间内流过指定平面区域的体积；v：流体流过指定平面区域时的速度；A：指定平面区域的面积

我们对血管以及血液进行微元分析。取血管上某处dL长的部分，假设血管初始的半径是R0，这时血液在血管中衡定流动，则不会产生血压，且此时流量为Q0。射入血液后血管的半径就是一个变量R，血液流过区域的横截面就是半径为R的圆的面积了，最终代入基础的物理学公式，得 p=2k sqrt(πv/Q) |1- sqrt(Q0/Q)| 从上面的公式，我们可以得知，血管特定点的血压与血液流动的速率和血液流量有关。有了这个公式，我们不但有了机器测量脉搏波的数学基础，还可以合成各种脉搏波形，为后续理论分析脉搏波提供试验数据。
  3.2 脉搏信号模型 1948年，Claude Shannon在《Bell System Technical Journal》上发表了《AMathematical Theory of Communication 》的论文，建立了信息论学科。短短六十多年，它已经广泛应用于各个领域。通信系统以信息论为基础，它是完成信息传输过程的技术系统的总称。 当硬件传感器接收到脉搏跳动的压力后，会通过线路通信，将得到的压力以电压值的形式与计算机进行交互，一串数据样本就存储到计算机里了。对脉诊仪和计算机所组成的通信系统进行分析，不难得到压力值数据就是信号了，信道则主要是仪器和计算机间的连接线。 脉搏波是一种波，那么物理中研究波动的知识同样适用于它。为了让拥有时间和波幅二维空间的脉搏波更具细节性，很自然地联想到数学上的级数。其中，傅立叶级数最令人印象深刻，它将一个函数拆解为许多小谐波的组合，使函数拥有了更多细节。更具广泛性地讨论，傅立叶变换便产生了。由于傅立叶变换要求函数具有一定的收敛性，奥地利数学家Johann Radon在1917年提出了著名的拉东变换，而其最常用的形式则是Haar小波，它延续了傅立叶变换在数据分析上的出 {MOD}表现，并消除了傅立叶变换原有的限制性。傅立叶级数在经常使用之后，就逐渐演化成更通用的傅立叶变换。为了简化模型，这里采用高效易用的傅立叶变换X(k) = sum(x(n)*exp(-2πikn/N)), n=0,1,..,N-1去处理数据。
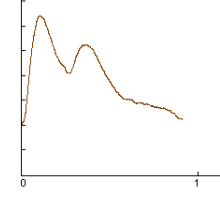
医管家多功能辨证仪在实验中使用，全文中所有实测数据都是通过它进行采集的。它每秒采集压力值样本量为1830，就是有∆x=1/1830；该仪器每次共收集N=109800个数据。所以最终有
ξ=k/60 这个公式在实现傅立叶变换时很有用，可以将k看成计算机程序的数组中某元素的序号，而ξ则是频率值。如果想知道一组数据经过离散傅立叶变换后1Hz谐波的权值，只需要查看计算机程序对应数组中第60号元素的值就可以了。

由于人体听力的范围一般在20Hz ~ 20000Hz，正常人通常是听不见自己的器官随着血液波动而发出声音的。实验证实，人体器官随着血液波动，其振动频率在0 ~ 16Hz。所以我们需要对得到的数据进行滤波，即把不需要的信息全部去处掉。由最近得到的公式，不难算出 k∈{[0,960]∩Z} 定义k的最大值为K，则此时K=960。这个范围初步确定了进行离散傅立叶变换所需要的计算量。本节主要探讨了数据的前期处理，至于数据后期的自动分析，将在第五节进行详细讨论。

4. 软件第一部分：脉搏波处理

4.1 信号数据文件的分析

医管家多功能辨证仪有一套自带的软件包，它不但负责收集仪器传回的数据，还可以对数据进行常规的分析。但是该软件并没有提供相应的分析结果输出接口，所以数据处理还须要自己完成。

多次进行测量实验后发现，医管家多功能辨证仪配套软件包在执行测量任务后会在特定文件夹创建一个扩展名为DAT的文件，文件大小固定为219624字节。分析后发现，该文件存储了109800个16位整数，另加5个32位整数，存储着用户选取的一个周期波形的文件偏移量。

4.2 病灶分析算法

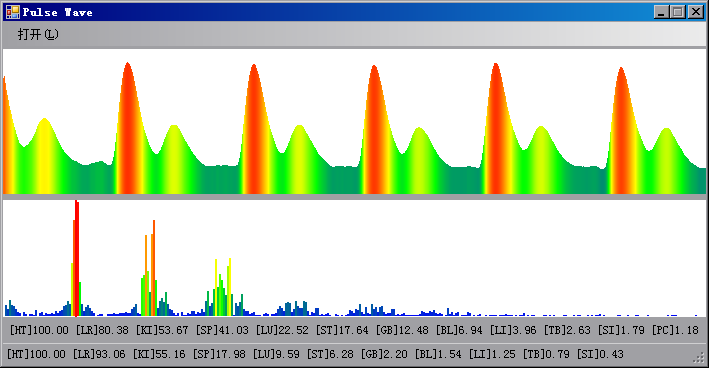
王维工教授在《气的乐章》最后一章中给出了一个年轻正常人脉搏波在频域下的参考标准值。以此为基础便很容易就能得到一些简单的病灶分析算法。

相关器官 能量振幅比率(%) 心脏 100.000000
肝脏 80.388410
肾脏 53.670830
脾脏 41.030000
肺脏 22.520010
胃脏 17.643980
胆脏 12.482200
膀胱 6.949338
大肠 3.963352
三焦 2.626356
小肠 1.791302
心包 1.183306

这十二组参考标准值可以用一个向量s来表示，令表示人体状态的这组值为m。要得到m，必须从离散傅立叶变换后的数据中取值，如何得到每个谐波的值呢？心谐波的频率当然是脉搏波的频率，因为最初的数据文件提供了一个周期中五个点的文件偏移量，每个数据之间间隔了1/1830秒，所以很容易得到一个脉搏波的周期T，那么自然就得到了其频率f，因为
f=1/T 利用第三节推出的公式
ξ=k/60
可以得到数据在数组中存储的位置，从而得到心谐波能量振幅比率。

由于心谐波生肝谐波，肝谐波生肾谐波，肾谐波生脾谐波，依次类推，凭借着谐波频率倍数的关系，很容易就能将所有比率值找到，并得到最终的m。 接着我们就可以定义各个器官的状态e了，有
e(i)=(m(i)-s(i))/s(i) ,i=心,肝,肾,脾,肺,胃,胆,膀胱,大肠,三焦,小肠,心包
当器官的e值大于0时，器官能量有剩余；当器官的e值小于0时，器官能量不足。按照《气的乐章》中的理论，器官能量有剩余是暂时可以不用处理的，我的思考是，在一定范围可以，大于一个阈值就应该算是上火或者其他情况了。最要注意的就是器官能量不足，说明它们已经开始缺血了，缺血意味这循环不通畅，氧气不能及时送到器官，细菌很多是厌氧的，于是它们便可以大量繁殖。当然，值得注意的是这样计算的话，心谐波永远不会得出有问题，所以这是这个算法最大的弊端。这就是病灶分析算法。

5. 数学第二部分：中医信息模型

5.1 中药经验模型

当代中药文献中充斥了大量的化学分析，各种有机物堆砌在一起，让人眼花缭乱。随着结构生物的迅猛发展，人们正在尝试建立物质更具体的模型。目前，我们对这些零散的模型只能望而却步，没有办法实际操作它们。一个是模型多而杂乱，没有一套统一的系统；另一方面由于势场函数计算的复杂性，导致很多模型必须要依赖高负荷的科学计算，这要有大型机或分布式网络的硬件支持，同时对可信计算的要求也非常高。不能从这些大规模药物的数据得到结果，我们就从另一个角度去思考中药。

现阶段我们只能以一个纯粹经验主义者的身份去分析中药。对古籍中药的描述进行概括，发现在大量文献记载中都有药物寒热、归经和味道。药物味道的分析会牵扯过多经络知识，所以这里我们仅对药物寒热和归经进行讨论。
我们将把重点先放在中药的一个基本假设上，并将其当作一个公理，贯穿在后面的理论中。假设（1）中药的寒热中，寒代表达到减少能量的效果，热则代表增加能量的效果；（2）归经则是指明药物会对哪种器官的谐波造成影响。在假设（1）中，寒热作为阴阳两种极端，我们所能和刚才的病灶分析中参数联系起来的，只有能量的强弱了，暂时并没有实验基础。而假设（2）则是背景的，因为药物归经后，说明吃的药物可以将血液很大程度地送到相应的器官，使得相应器官能得到比原先更多的氧气，于是缺氧的症状会相对减弱，器官的振动则会恢复正常，其谐波的能量也自然就改善了。 根据这两个假设，我们便可以建立起中药的数学模型，即一个表示药物治疗作用的向量
med≡(心，肝，肾，脾，肺，胃，胆，膀胱，大肠，三焦，小肠，心包)
该向量表示药物归经，比如某药物归心经，那么心值就为1，不归心经则为0；并且还需要有一个函数v去表示药物的寒热程度，其值1.0表示热，0.5表示温，0表示平，-0.5表示凉，-1.0表示寒。

5.2 方剂统计模型

基于中药经验模型的假设，我们将得到方剂的经验统计模型。方剂中，用药物时都有各自的剂量，定义方剂治疗作用模型为
p≡sum(w*med),
med∈M
M为方剂中所含有的药物，w为某个药物的重量，和符号表示所有药物混合在一起。

经过不少方剂的测试，我们发现方剂主要治疗对象所对应的p中的值是p中最大的元素。比如六味地黄丸滋补肝肾，方剂组成为熟地黄24g，山萸肉12g，干山药12g，泽泻9g，牡丹皮9g，茯苓9g，则 med(熟地黄) = (0,1,1,0,0,0,0,0,0,0,0,0)
med(山萸肉) = (0,1,1,0,0,0,0,0,0,0,0,0)
med(干山药) = (0,0,1,1,1,0,0,0,0,0,0,0)
med(泽泻) = (0,0,1,0,0,0,0,1,0,0,0,0)
med(牡丹皮) = (1,1,1,0,0,0,0,0,0,0,0,0)
med(茯苓) = (1,0,1,1,0,0,0,0,0,0,0,0)
p(六味地黄丸) = (18,45,75,21,12,0,0,9,0,0,0,0)
p中肝对应的值为45和肾对应的75分别为整个向量中第二大和最大的数。

再举一个例子，达原饮开达膜原，辟秽化浊，方剂组成为槟榔6g，厚朴3g，草果仁1.5g，知母3g，芍药3g，黄芩3g，甘草1.5g med(槟榔) = (0,0,0,0,0,1,0,0,1,0,0,0)
med(厚朴) = (0,0,0,1,1,1,0,0,1,0,0,0)
med(草果仁) = (0,0,0,1,0,1,0,0,0,0,0,0)
med(知母) = (0,0,1,0,1,1,0,0,0,0,0,0)
med(芍药) = (0,1,0,1,0,0,0,0,0,0,0,0)
med(黄芩) = (0,0,0,1,1,1,1,0,1,0,1,0)
med(甘草) = (1,0,0,1,1,1,0,0,0,0,0,0)
p(达原饮) = (1.5,3,3,12,10.5,18,3,0,9,0,3,0)
辟秽化浊可以看出对脾胃影响较大，脾对应的值是12，胃对应的为18，是p中最大的两个；对于开达膜原，虽然不是特别清楚它的含义，但从p来看，很可能是在说改善肺部的状况，因为批紧接着就是肺的10.5。

6. 软件第二部分：药物治疗分析

6.1 数据库构建

数据库的结构设计得相当简单，药物表就是存储序号ID、药物名称NAME、药物寒热MILD、药物归经的十二个布尔型变量HT, LR, KI, SP, LU, ST, GB, BL, LI, TB, SI, PC。方剂表则更为简洁，有序号ID、方剂名称NAME，方剂组成PRESCRIPT，其中方剂组成存储的是一个字符串。这个字符串中，一个药物有3个值，分别对应药物序号、药物用量和一个无用的预留值，以逗号隔开；每个药物间的数据用分号分割。

考虑到这是一个软件原型，并没有特别大量的数据，于是数据库使用的是轻量级的SQLite实现。它不需要任何安装和配置，所以在原型演示上有利；它操作起来方便快捷，易于上手；它使用SQL语句查询数据，所以可以很容易将它更换成正规的数据库，即可移植性很高。 数据收集方面，库中直接选用了全国高等中医药院校规划教材系列的《中药学》和《方剂学》。其中《中药学》中几乎所有中药都收录在了数据库中，共计478味中药；《方剂学》提供了68种配方，都是每种类型中比较有代表性的。

6.2 方剂推荐算法

自动推荐方剂算法就是一个打分函数。承接第三章节的模型，机体目前处于状态为m，与参考标准s对每一谐波的状况计算后得到差值比e，吃了方剂后，机体状态会变为m’，再与参考标准比对得到e’，如果e’优于e，那么这个方剂就可以推荐出来。这是方剂推荐的基本思路。
现在要求解出m’和e’。仿照第三章节病灶分析算法，可以得到
e’(i)=(m’(i)-s(i))/s(i)，i ∈ O = {心，肝，肾，脾，肺，胃，胆，膀胱，大肠，三焦，小肠，心包}。
这个公式是服用了方剂p后得到的状态，所以
m’=f(m,p)
现在我们将机体状况和方剂治疗状况转换成了可比较的两个向量e和e’，再定义打分函数score(x)。其中score(x)越大表示病人机体状况越差。当score(e)大于score(e’)时，就说明方剂p有疗效了，疗效评分为
ϵ≡(score(e’)-score(e))/(score(e))×100
这样遍历方剂数据，将方剂的分数算出；舍弃分数比基本分大的方剂，接着将得到的方剂按评分降序排列，得到方剂推荐列表。方剂推荐算法完成。

7. 结论

最终通过得到的全部数学模型，将其一一转化为计算机程序。通过Microsoft Visual Studio 2005集成开发环境，使用C#语言，开发出一个与脉诊仪配套使用的脉搏波分析软件。最终通过得到的全部数学模型，将其一一转化为计算机程序。通过Microsoft Visual Studio 2005集成开发环境，使用C#语言，开发出一个与脉诊仪配套使用的脉搏波分析软件。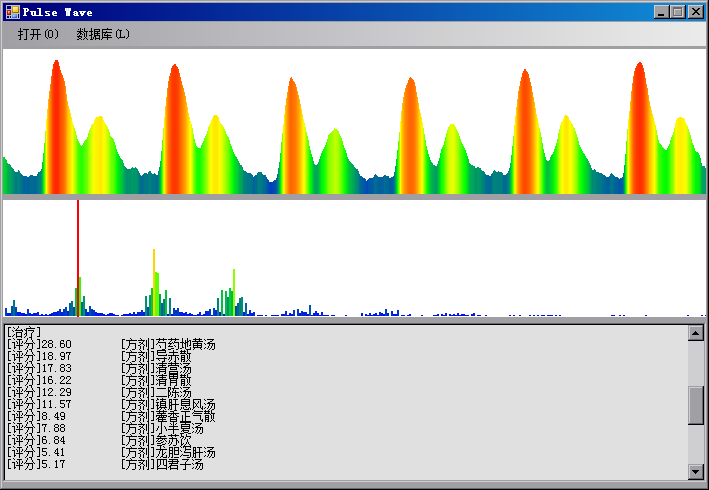

参考文献

[1] 王唯工. 气的乐章[M]. 人大出版社, 2006
[2] 罗志昌, 张松, 杨益民. 脉搏波的工程分析与临床应用[M]. 科学出版社, 2006
[3] 王唯工. 水的漫舞[M]. 中国人民大学出版社, 2007
[4] 李家邦. 中医学[M]. 第六版. 人民卫生出版社, 2005
[5] 潘欣祥, 马芳杰. 神奇养生[M]. 南方出版社, 2008
[6] Wikipedia. Pressure Sensor[OL/A]. http://en.wikipedia.org/wiki/Pressure_sensor, 访问时间：2012.01
[7] Rodger E. Ziemer, William H. Tranter. Principles of Communications[M]. Wiley, 2009
[8] Gallica Fourier, Jean Baptiste Joseph. Oeuvres de Fourier[M]. Gauthier-Villars, 1888
[9] Wikipedia. Fourier Seris[OL/A]. http://en.wikipedia.org/wiki/Fourier_series, 访问时间：2012.03
[10] Wikipedia. Fourier Transform[OL/A]. http://en.wikipedia.org/wiki/Fourier_transform, 访问时间：2012.03
[11] Gerald Kaiser. A Friendly Guide to Wavelets[M]. Birkhäuser, 1994
[12] 黄载禄, 殷蔚华, 黄本雄. 通信原理[M]. 科学出版社, 2007
[13] Colin Ware. Information Visualization - Perception for Design[M]. 2nd ed. Elsevier, 2004
[14] Wikipedia. RGB Color Model[OL/A].
http://en.wikipedia.org/wiki/RGB_color_model, 访问时间：2012.03
[15] 周仁郁. 中医药数学模型[M]. 中国中医药出版社, 2006
[16] 万德光, 肖崇厚. 中药化学[M]. 上海科学技术出版社, 1997
[17] 高学敏. 中药学[M]. 中国中医药出版社, 2002
[18] 邓中甲. 方剂学[M]. 中国中医药出版社, 2003
[19] 邓中甲. 方剂学[M]. 上海科学技术出版社, 2008