本文为转载,原博客地址为:http://blog.csdn.net/jorg_zhao/article/details/51328966

那么到底什么是病态问题呢? 给定图像f(x),如果x从x增加到x*,则△x=x-x*,其相对误差是△x/x,f(x*)的相对误差是(f(x)-f(x*))/ f(x),因此相对误差比是 |(f(x)-f(x∗) / f(x) )| / | Δx/x |= C_p C_p叫做条件数condition number。如果条件数足够大,相对误差比也将会很大,这种问题叫病态问题,简言之就是自变量变化,结果就会出现大的变化,从而导致问题不易求解。 那么到底如何求解病态问题呢?
病态问题必须要添加正则项或先验,有关正则项的研究,已经有很多相关论文给出了求解方法,在龚元浩老师的PPT中有下面的总结和描述:
分段常数、分段线性和分段平滑的意思,按我的理解,现在正在看相关的论文,还处在刚开始接触的阶段,可能会有误,在图像分割问题中,如果将原始图像有意图的分割成2个区域,那么每个区域中的像素值是近似的,在过两个分割区域的边界时,像素值变化是剧烈的,分段常数就是说分割之后的两个块区域的函数表达式是分段常数的,不同的区域有不同的值,那么引申而来的,分段线性就是分割函数是分段线性的,分段平滑也类似的理解。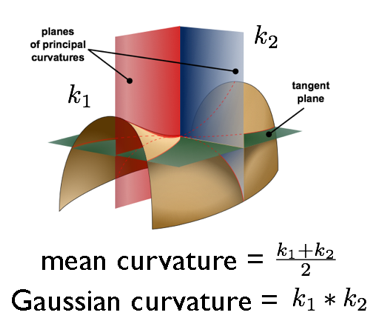
曲面上的一点有一切平面tangent plane,此点处会有各个方向上的曲率,但是必然会有最大主曲率和最小主曲率,k1是最小主曲率,k2是最大主曲率,则平均曲率和高斯曲率的定义如上,具体的微分几何求解过程可以参考附件中的文档《曲率滤波---微分几何理论基础》。
这里,T[y(x), delta y]对delta y而言是线性泛函,即主要部分,而后一项,是相对于max|delta y|的高阶无穷小,那么泛函的变分表示为: delta Q = T[y(x), delta y] 具体的详细过程请参考附件《曲率滤波---微分几何理论基础》。
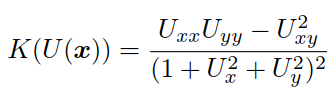
在去噪算法中,用到的变分模型是,总绝对高斯曲率变分模型: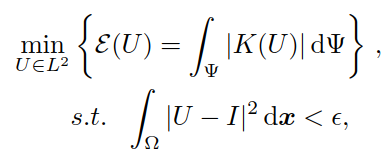
其中,E(U)是高斯曲率能量,e是演化终止阈值,是个很小的数。 很多文献已经给出了上述问题的求解方法,一般是基于扩散的方法,即diffusion-based algorithm,主要是通过加入伪时间t,直到达到稳定状态或满足终止条件: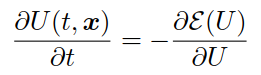
初始条件U(t=0,x) = I(x)。这个模型已经通过使用几何流的方法推广到各向异性扩散方法中(Lee and Seo, 2005):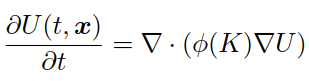
具体的算法可以参考相关文献,这里不详细介绍了。 但是,扩散的方法有两个问题: 1) 收敛速度慢 收敛速度慢,演化时间复杂度从而就高,迭代次数一般就会很高,会达到2,3000。 2) 平滑度的要求 从数值上要显式计算高斯曲率,因而必须要求图像是二次可微的,即可以对图像求微分。
本文提到的高斯曲率滤波器,由于无需显式计算高斯曲率,大大降低了计算复杂度,反而从微分几何的角度,由图像的分段可展曲面去估计图像,这在处理此问题时,就会有如下优势: 1) 在时间和收敛度上,比之前的算法都要快! 2) 滤波器无需显式计算高斯曲率! 3) 滤波器是无参的(备:迭代次数的参数不算在内的话,算无参),且易于实现,还可并行实现,matlab有40行代码,c++少于100行代码。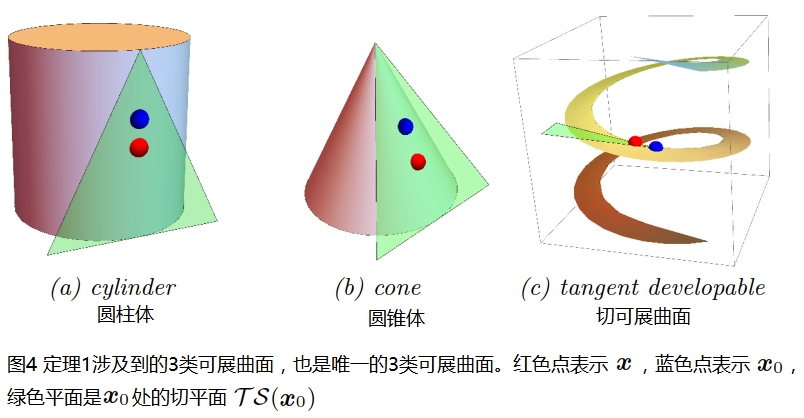
另外,微分几何中有定理1: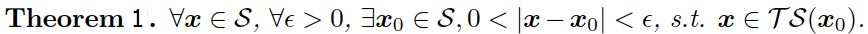
此定理的证明过程可以参考龚元浩老师的原文第134页6.1.2.1节的证明。前面我们已知,二维图像中的高斯曲率定义为两个主曲率的乘积,定理1告诉我们的是,任何可展曲面,虽然只有3个可展曲面,其任意点处的高斯曲率为零。因此,最小化其中任意一个主曲率,就相当于最小化高斯曲率! 定理1的结论即是高斯曲率滤波器的理论基础! 由此,我们即可实现高斯曲率的最小化而无需进行高斯曲率的显式计算,即如下式所示,最小化其中较小的主曲率即可实现高斯曲率的最小化: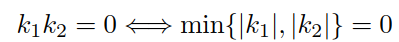
这种划分实际上有3个好处: 1) 去除了相邻像素之间的依赖性; 2) 由于相邻像素之间的独立性,当前像素值的更新可以利用周围已更新的像素值,因为4类像素的更新是独立进行的,没有先后次序,所以在更新某一类像素时,可以利用周围已经更新过的某些类像素值; 3)在3×3局部窗口中,所有切平面可以枚举出来(切平面如何表示后续会介绍),因此近邻投影(proximal projecting)能够用于使得图像曲面更加可展,这就意味着可以局部的降低高斯曲率; 通过定理1可知,我们需要将原始图像曲面U(x)投影到U`(x),使得U`(x)在相邻像素的闭合切平面上。 首先,确定如何表示其切平面; 然后,确定如何选取投影方法;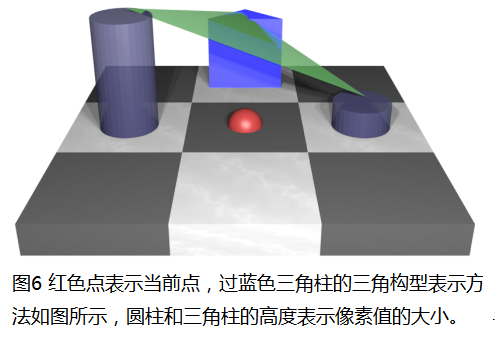
这是在此局部窗口中的一个三角切平面,其他的枚举示例下一小节会介绍,得到此切平面之后,我们将红 {MOD}点,即当前点投影到绿 {MOD}切平面上,就可以得到当前点到切平面的距离,如图7所示: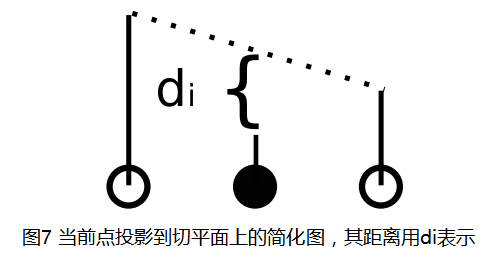
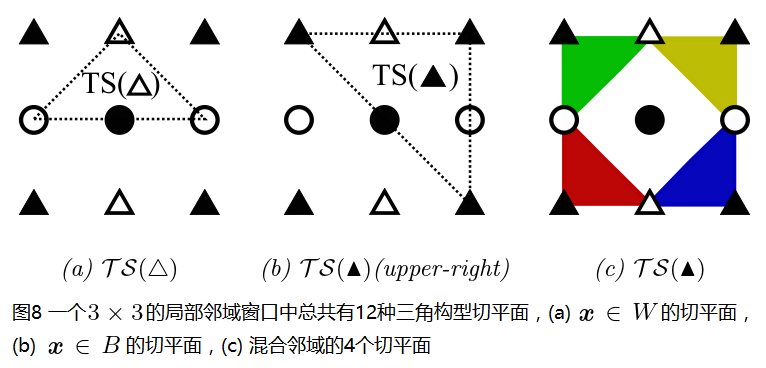
图8(a)给出了一个示例,实际上,以黑 {MOD}圆形点为中心点,切平面过白 {MOD}点的三角构型切平面还有3种,也就是说图8(a)中的切平面共有4种,如图9所示: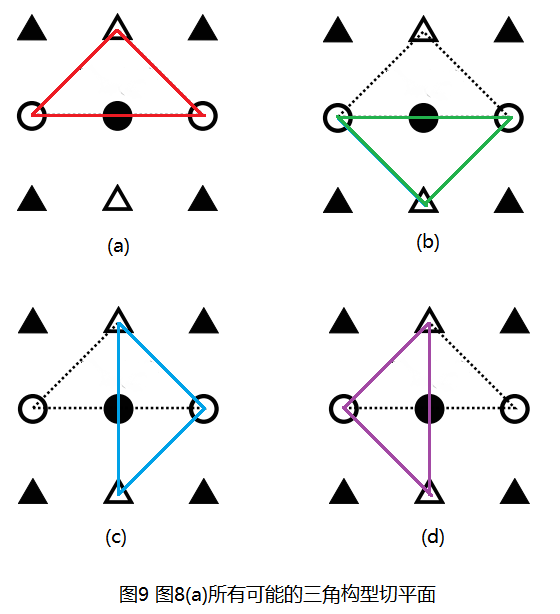
类似的图8(b)也有4种,图8(c)有4种,其全部给出,如此,在一个3×3的局部窗口中,三角构型切平面共有12种情况,但是仔细看图6和图7可以看出,到切平面的距离di的实际情况没有12种,按照图7所示,图8可以简化为下图: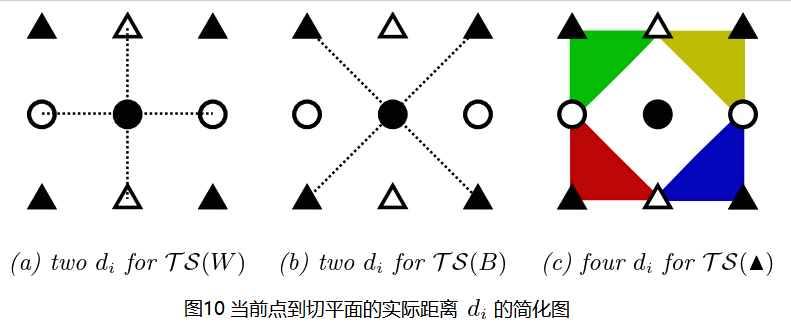
以图10(a)为例说明一下,黑 {MOD}圆点到切平面的距离实际上就是黑 {MOD}圆点到 ”白 {MOD}圆-黑 {MOD}圆-白 {MOD}圆” 线段的距离,这种距离看图7应该可以理解,图10(b)(c)均好理解,这里不赘述了。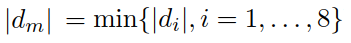
然后,利用下式对原始图像的三维曲面进行计算: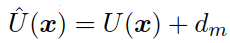
完整的算法数值实现伪代码如图11所示:
图11对应于原始论文的第140页 Algorithm 11 。需要说明的是,基于Euler Theorem,我们有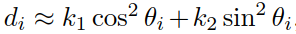
其实,这个欧拉定理原始论文中也是直接给出的,没有参考文献可以参考,暂时这么记住吧! 上式中,k1 k2是两个主曲率,theta(i) 是到主平面的角度,主平面可以参考图3理解。因此,如果角度采样theta(i) 在[-pi, +pi]内是足够致密的(dense enough),可得 | dm | ≈ min{| ki |},其中k1k2≥0,关于di的详细介绍在下一章节中会重点介绍。 由于此四类像素是相互独立的,其迭代是互不影响的,因而可以并行运算。
由于此四类像素是相互独立的,其迭代是互不影响的,因而可以并行运算。
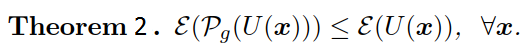
证明:4类像素只需要证明其中一种即可,其余类似,
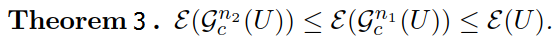
换句话说,高斯曲率能量是相对于n的单调函数,又能量肯定是对于零的,由单调有界定理可知,高斯曲率滤波器算法2是收敛的。
前言
大概是两个月之前开始学习曲率滤波,从一个完全一无所知的状态开始学习的,包括微分几何等相关基础知识也是未曾学习过的,从初学者的角度学习曲率滤波。现在新加坡南阳理工大学任教的龚元浩老师在其2015年博士论文中的第六章给出了理论基础和实际的应用,包括去噪平滑等,首先针对性的构造了高斯曲率滤波器,给出了详细的理论基础,主要是从微分几何的角度分析了其思想的根本来源,简言之就是通过某种合理的像素点投影映射将原始图像3维曲面映射成可展曲面,这里有个重要的知识点是:最小化平均曲率Mean Curvature会导致极小曲面,最小化高斯曲率Gaussian Curvature会导致可展曲面,可展曲面能够很好的保留边缘信息,因此就涉及了文中所说的ADAP-As Developable As Possible,使曲面尽可能可展。这是最基本的思想,具体的展开学习下面开始,或有理解错误的地方,才疏学浅,难免有误,见谅!1. 概述
曲率滤波解决的问题其实是求解变分模型,相比之前的扩散方法或梯度下降法等,曲率滤波是从微分几何的角度最小化相关曲率来实现最小化正则项的方法,作为一个初学者,在真正学习曲率滤波之前,必须要了解的几个问题,归纳整理一下,也是我在学习过程中,必须要迈过去的坎。1.1 适定性/病态问题
适定性问题,英文是well-posed problem,病态问题,英文是ill-posed problem,从离散样本中估计真实图像通常都是病态问题,比如去模糊deblurring,点云图像的曲面拟合estimated surface from point image
那么到底什么是病态问题呢? 给定图像f(x),如果x从x增加到x*,则△x=x-x*,其相对误差是△x/x,f(x*)的相对误差是(f(x)-f(x*))/ f(x),因此相对误差比是 |(f(x)-f(x∗) / f(x) )| / | Δx/x |= C_p C_p叫做条件数condition number。如果条件数足够大,相对误差比也将会很大,这种问题叫病态问题,简言之就是自变量变化,结果就会出现大的变化,从而导致问题不易求解。 那么到底如何求解病态问题呢?
病态问题必须要添加正则项或先验,有关正则项的研究,已经有很多相关论文给出了求解方法,在龚元浩老师的PPT中有下面的总结和描述:

分段常数、分段线性和分段平滑的意思,按我的理解,现在正在看相关的论文,还处在刚开始接触的阶段,可能会有误,在图像分割问题中,如果将原始图像有意图的分割成2个区域,那么每个区域中的像素值是近似的,在过两个分割区域的边界时,像素值变化是剧烈的,分段常数就是说分割之后的两个块区域的函数表达式是分段常数的,不同的区域有不同的值,那么引申而来的,分段线性就是分割函数是分段线性的,分段平滑也类似的理解。
1.2 微分几何基础知识
从“曲率滤波”字面意思就能看出,关键词是曲率,曲率的概念在高等数学中简单的提及到,但是当初的知识点无法支撑我们现在所要研究的领域,因此,简单的对曲率的学习是必不可少的,本文所及的曲率有两个重要类型---高斯曲率Gaussian Curvature和平均曲率Mean Curvature,如图3:
曲面上的一点有一切平面tangent plane,此点处会有各个方向上的曲率,但是必然会有最大主曲率和最小主曲率,k1是最小主曲率,k2是最大主曲率,则平均曲率和高斯曲率的定义如上,具体的微分几何求解过程可以参考附件中的文档《曲率滤波---微分几何理论基础》。
1.3 变分学基础
在一般高等数学框架中,我们都知道微分的概念,一般的dy=f'(x)dx,但是这不是最基础的形式,在我整理的文档《曲率滤波---变分学基础》中, 可以得到这样的结论: △y = f'(x) △x + O(△x) 可见,f'(x) △x是函数增量的主要部分,也是其线性部分,即“线性主要部分”,我们把函数增量的线性主要部分f'(x) △x叫做函数的微分,这才是微分的本质。 那么什么是变分呢? 变分指的是在泛函理论中的“微分”。 那么什么是泛函呢? 把具备某种性质的函数的集合记作D,对于D中的任何函数f(x),即对任意的f(x)∈D,变量Q都有唯一的值与之相对应,那么变量Q叫做依赖于f(x)的泛函,记为 Q = Q[f(x)] 或 Q = Q[f] 简言之就是一般的函数自变量是x,泛函的自变量是函数f(x),微分是一般函数的自变量x的微增量导致f(x)的变化,变分是泛函中的自变量f(x)的微增量导致的Q的变化。 根据一般函数的微分本质的表达方式,泛函中的微分本质的表达方式也可以类似的描述: △Q = T[y(x), delta y] + beta[y(x), delta y]这里,T[y(x), delta y]对delta y而言是线性泛函,即主要部分,而后一项,是相对于max|delta y|的高阶无穷小,那么泛函的变分表示为: delta Q = T[y(x), delta y] 具体的详细过程请参考附件《曲率滤波---微分几何理论基础》。
2. 高斯曲率滤波器
2.1 序言
根据1.2所述的相关微分几何知识,我们知道高斯曲率的定义,但是在二维图像中,高斯曲率的定义则是: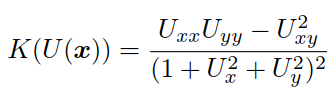
在去噪算法中,用到的变分模型是,总绝对高斯曲率变分模型:
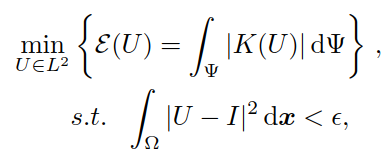
其中,E(U)是高斯曲率能量,e是演化终止阈值,是个很小的数。 很多文献已经给出了上述问题的求解方法,一般是基于扩散的方法,即diffusion-based algorithm,主要是通过加入伪时间t,直到达到稳定状态或满足终止条件:
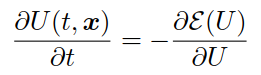
初始条件U(t=0,x) = I(x)。这个模型已经通过使用几何流的方法推广到各向异性扩散方法中(Lee and Seo, 2005):
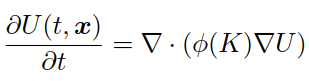
具体的算法可以参考相关文献,这里不详细介绍了。 但是,扩散的方法有两个问题: 1) 收敛速度慢 收敛速度慢,演化时间复杂度从而就高,迭代次数一般就会很高,会达到2,3000。 2) 平滑度的要求 从数值上要显式计算高斯曲率,因而必须要求图像是二次可微的,即可以对图像求微分。
本文提到的高斯曲率滤波器,由于无需显式计算高斯曲率,大大降低了计算复杂度,反而从微分几何的角度,由图像的分段可展曲面去估计图像,这在处理此问题时,就会有如下优势: 1) 在时间和收敛度上,比之前的算法都要快! 2) 滤波器无需显式计算高斯曲率! 3) 滤波器是无参的(备:迭代次数的参数不算在内的话,算无参),且易于实现,还可并行实现,matlab有40行代码,c++少于100行代码。
2.2 理论阐述
可展曲面可由其切平面局部估计得到,如图4所示:
另外,微分几何中有定理1:
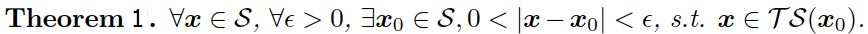
此定理的证明过程可以参考龚元浩老师的原文第134页6.1.2.1节的证明。前面我们已知,二维图像中的高斯曲率定义为两个主曲率的乘积,定理1告诉我们的是,任何可展曲面,虽然只有3个可展曲面,其任意点处的高斯曲率为零。因此,最小化其中任意一个主曲率,就相当于最小化高斯曲率! 定理1的结论即是高斯曲率滤波器的理论基础! 由此,我们即可实现高斯曲率的最小化而无需进行高斯曲率的显式计算,即如下式所示,最小化其中较小的主曲率即可实现高斯曲率的最小化:
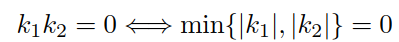
2.3 域分解方法
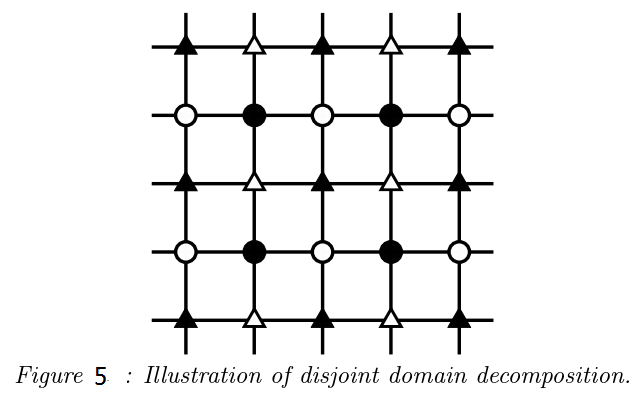
局部最小化主曲率绝对值的较小者,受限于相邻像素之间的关联性,因此,提出了一种域分解方法,以去除相邻像素之间的依赖性。 如图5所示,将二维图像中的像素点分成4类,即水平方向和垂直方向上的同类像素点均不相邻:
这种划分实际上有3个好处: 1) 去除了相邻像素之间的依赖性; 2) 由于相邻像素之间的独立性,当前像素值的更新可以利用周围已更新的像素值,因为4类像素的更新是独立进行的,没有先后次序,所以在更新某一类像素时,可以利用周围已经更新过的某些类像素值; 3)在3×3局部窗口中,所有切平面可以枚举出来(切平面如何表示后续会介绍),因此近邻投影(proximal projecting)能够用于使得图像曲面更加可展,这就意味着可以局部的降低高斯曲率; 通过定理1可知,我们需要将原始图像曲面U(x)投影到U`(x),使得U`(x)在相邻像素的闭合切平面上。 首先,确定如何表示其切平面; 然后,确定如何选取投影方法;
2.4 切平面的表示方法
其实,有很多种切平面的表示方法(这在后续实际的应用上体现出了这种表示方法的多样性),在本小节中,选取的是三角构型用于表示曲面的切平面,下面以黑 {MOD}圆x与其3×3邻域N(x)为例,如图6所示:
这是在此局部窗口中的一个三角切平面,其他的枚举示例下一小节会介绍,得到此切平面之后,我们将红 {MOD}点,即当前点投影到绿 {MOD}切平面上,就可以得到当前点到切平面的距离,如图7所示:

2.5 枚举所有类型的投影
为了在局部窗口N(x)中找到最小的投影距离di,需要将所有可能的三角构型切平面枚举出来,如图8所示:
图8(a)给出了一个示例,实际上,以黑 {MOD}圆形点为中心点,切平面过白 {MOD}点的三角构型切平面还有3种,也就是说图8(a)中的切平面共有4种,如图9所示:

类似的图8(b)也有4种,图8(c)有4种,其全部给出,如此,在一个3×3的局部窗口中,三角构型切平面共有12种情况,但是仔细看图6和图7可以看出,到切平面的距离di的实际情况没有12种,按照图7所示,图8可以简化为下图:

以图10(a)为例说明一下,黑 {MOD}圆点到切平面的距离实际上就是黑 {MOD}圆点到 ”白 {MOD}圆-黑 {MOD}圆-白 {MOD}圆” 线段的距离,这种距离看图7应该可以理解,图10(b)(c)均好理解,这里不赘述了。
2.6 最小投影算子
图2.5节可知,当前点到切平面的投影总共有8种,即当前点到切平面的距离共有8种,{di, i=1,2,...,8},这里使用8种投影距离的最小值作为投影算子,更确切的说,令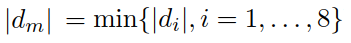
然后,利用下式对原始图像的三维曲面进行计算:
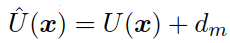
完整的算法数值实现伪代码如图11所示:

图11对应于原始论文的第140页 Algorithm 11 。需要说明的是,基于Euler Theorem,我们有
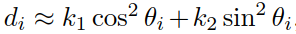
其实,这个欧拉定理原始论文中也是直接给出的,没有参考文献可以参考,暂时这么记住吧! 上式中,k1 k2是两个主曲率,theta(i) 是到主平面的角度,主平面可以参考图3理解。因此,如果角度采样theta(i) 在[-pi, +pi]内是足够致密的(dense enough),可得 | dm | ≈ min{| ki |},其中k1k2≥0,关于di的详细介绍在下一章节中会重点介绍。
2.7 高斯曲率算子
由于之前我们只是针对某一类,比如黑 {MOD}三角形进行的详细介绍,所以联合其他三类的投影操作就构成了此高斯曲率滤波器,如图12所示: 由于此四类像素是相互独立的,其迭代是互不影响的,因而可以并行运算。
由于此四类像素是相互独立的,其迭代是互不影响的,因而可以并行运算。
2.8 收敛性证明
在证明高斯曲率滤波器之前,首先证明每一步最小投影算子都可以降低高斯曲率能量E(U),然后再证明高斯曲率滤波器能够降低总能量。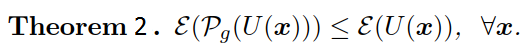
证明:4类像素只需要证明其中一种即可,其余类似,

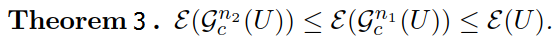
换句话说,高斯曲率能量是相对于n的单调函数,又能量肯定是对于零的,由单调有界定理可知,高斯曲率滤波器算法2是收敛的。