在一个线性时不变系统(LTI)中,当输入信号x(n)随着时间而作用到系统中,y(n)作为x(n)在时间序列中作用在系统中的响应。
先从离散系统分析,卷积形式如下:
 先考虑有限因果系统的信号输入,可得:
先考虑有限因果系统的信号输入,可得:

从式子可以得到,y(0)=x(0)h(0), y(1)=x(0)h(1)+x(1)h(0) ........ 其中:x(0),x(1),,,,,x(n),为时间0,时间1,...,时间n 时刻中,作用在系统的输入信号。 h(n)则为单位脉冲函数测出的系统传递函数,h(n)为当脉冲函数作用到系统中而表现出来的系统响应随时间而变化的特性。
因此,假如在0时刻输入信号为脉冲信号,那么在n时刻系统的响应y(n)=x(0)h(n)。 [ x(n)=0 n/=0] 由此,当输入信号为一般信号,则可得:y(n)=x(0)h(n)+x(1)h(n-1)+...+x(n)h(0) 则可写成为卷积形式y(n)=x(n)*h(n) 也可设置卷积核来计算某序列中是否存在对卷积核的相似程度高或者可容性较大的部分。
理解完h(n),那么可假想,当n无穷大时,h(n)不趋于0,则系统的响应就会不断叠加信号的输入,输出趋于无穷大。 当h(n)为系统的传递函数时,因此可通过分析h(n)来评价系统的稳定条件。对连续系统也相似原理。
续: 对于线性时不变系统中的状态空间表达式如下:
可得解为: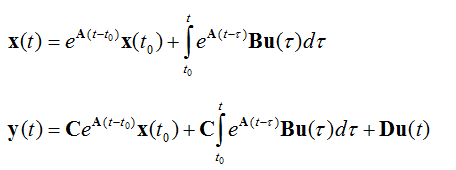
一般把 t0=0处理,则得到: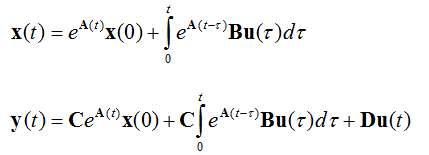
由公式可得,e^(At)项为系统的状态转移矩阵,表示系统中的状态随时间的变化,x(t)的积分项为对输入的卷积,因此系统的分阶段输入,即
在同一个系统中,上下公式只是表达形式不一样,但是结果是一样的,跟上面离散系统提到输入的卷积类似,这里可以把状态量作为系统的输出量,因此下式的第一项相当于t0状态在系统中经过了t1-t0的系统变换过程。
 先考虑有限因果系统的信号输入,可得:
先考虑有限因果系统的信号输入,可得:

从式子可以得到,y(0)=x(0)h(0), y(1)=x(0)h(1)+x(1)h(0) ........ 其中:x(0),x(1),,,,,x(n),为时间0,时间1,...,时间n 时刻中,作用在系统的输入信号。 h(n)则为单位脉冲函数测出的系统传递函数,h(n)为当脉冲函数作用到系统中而表现出来的系统响应随时间而变化的特性。
因此,假如在0时刻输入信号为脉冲信号,那么在n时刻系统的响应y(n)=x(0)h(n)。 [ x(n)=0 n/=0] 由此,当输入信号为一般信号,则可得:y(n)=x(0)h(n)+x(1)h(n-1)+...+x(n)h(0) 则可写成为卷积形式y(n)=x(n)*h(n) 也可设置卷积核来计算某序列中是否存在对卷积核的相似程度高或者可容性较大的部分。
理解完h(n),那么可假想,当n无穷大时,h(n)不趋于0,则系统的响应就会不断叠加信号的输入,输出趋于无穷大。 当h(n)为系统的传递函数时,因此可通过分析h(n)来评价系统的稳定条件。对连续系统也相似原理。
续: 对于线性时不变系统中的状态空间表达式如下:

可得解为:
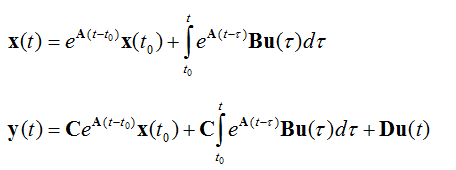
一般把 t0=0处理,则得到:
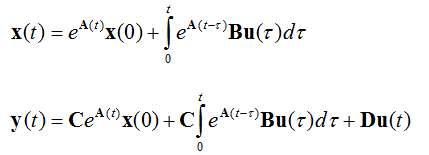
由公式可得,e^(At)项为系统的状态转移矩阵,表示系统中的状态随时间的变化,x(t)的积分项为对输入的卷积,因此系统的分阶段输入,即

在同一个系统中,上下公式只是表达形式不一样,但是结果是一样的,跟上面离散系统提到输入的卷积类似,这里可以把状态量作为系统的输出量,因此下式的第一项相当于t0状态在系统中经过了t1-t0的系统变换过程。