自适应算法所采用的最优准则有最小均方误差(LMS)准则,最小二乘(LS)准则、最大信噪比准则和统计检测准则等,其中最小均方误差(LMS)准则和最小二乘(LS)准则是目前最为流行的自适应算法准则。x(n)代表n时刻的输入信号,y(n)代表n时刻的输出信号,d(n)代表n时刻的期望信号,通过期望信号与输出信号之差e(n)来自动调节自适应滤波器的参数,使下一时刻的输出y(n+1)能够更加接近期望信号。

 利用最速下降算法,沿着性能曲面最速下降方向(负梯度方向)调整滤波器强权向量,搜索性能曲面的最小点,计算权向量的迭代公式为
利用最速下降算法,沿着性能曲面最速下降方向(负梯度方向)调整滤波器强权向量,搜索性能曲面的最小点,计算权向量的迭代公式为 μ为步长因子在最速下降算法中,为获得系统的最佳维纳解,需要知道输入信号和期望信号的相关信息,当期望信号未知时,就无法确定它们的相关特性,必须对梯度向量进行估计。LMS自适应算法直接利用瞬态均方误差对瞬时抽头向量求梯度
μ为步长因子在最速下降算法中,为获得系统的最佳维纳解,需要知道输入信号和期望信号的相关信息,当期望信号未知时,就无法确定它们的相关特性,必须对梯度向量进行估计。LMS自适应算法直接利用瞬态均方误差对瞬时抽头向量求梯度 可得,LMS自适应滤波算法权向量更新方程为:
可得,LMS自适应滤波算法权向量更新方程为: 由此可得传统LMS自适应滤波算法流程如下:
由此可得传统LMS自适应滤波算法流程如下: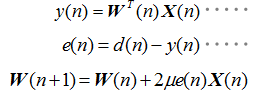
转载自知乎:lms算法在自适应滤波器中解决了什么问题? - Pandababe的回答 - 知乎https://www.zhihu.com/question/37548162/answer/92936555
另外,值得提出的是,LMS属于自适应滤波的一种。自适应滤波器有训练和工作两种过程。
在matlab中可以用dsp工具箱LMSFilter来创建系统对象进行调用。参考链接:[1] dsp.LMSFilter System object. matlab

 利用最速下降算法,沿着性能曲面最速下降方向(负梯度方向)调整滤波器强权向量,搜索性能曲面的最小点,计算权向量的迭代公式为
利用最速下降算法,沿着性能曲面最速下降方向(负梯度方向)调整滤波器强权向量,搜索性能曲面的最小点,计算权向量的迭代公式为 μ为步长因子在最速下降算法中,为获得系统的最佳维纳解,需要知道输入信号和期望信号的相关信息,当期望信号未知时,就无法确定它们的相关特性,必须对梯度向量进行估计。LMS自适应算法直接利用瞬态均方误差对瞬时抽头向量求梯度
μ为步长因子在最速下降算法中,为获得系统的最佳维纳解,需要知道输入信号和期望信号的相关信息,当期望信号未知时,就无法确定它们的相关特性,必须对梯度向量进行估计。LMS自适应算法直接利用瞬态均方误差对瞬时抽头向量求梯度 可得,LMS自适应滤波算法权向量更新方程为:
可得,LMS自适应滤波算法权向量更新方程为: 由此可得传统LMS自适应滤波算法流程如下:
由此可得传统LMS自适应滤波算法流程如下: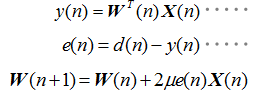
转载自知乎:lms算法在自适应滤波器中解决了什么问题? - Pandababe的回答 - 知乎https://www.zhihu.com/question/37548162/answer/92936555
另外,值得提出的是,LMS属于自适应滤波的一种。自适应滤波器有训练和工作两种过程。
- 在训练过程中,已知期望响应
,通过对权向量
的设计,使从输入信号
中得到的估计
在某种意义下最佳逼近
。
- 在工作过程中,权向量由训练过程得到,对未知输入(通常是随机信号)滤波得到响应信号。
在matlab中可以用dsp工具箱LMSFilter来创建系统对象进行调用。参考链接:[1] dsp.LMSFilter System object. matlab