//---------------------前言唠叨废话-------------------------------------------
本文的目标:让不是很了解DSP的小伙伴会用FFT(快速傅里叶变换),并知道怎么用代码实现FFT,不求甚解,但求works。
最近做项目用到FFT, 之前学的一直就不是很明白,现在用到了决定好好的把它搞懂。在中文网站上找了一些资料,发现讲的都不是很清楚,或者是我水平太低看不懂。后来还是在国外网站上找到了一篇讲深入浅出浅显易懂很接地气的文章。这里把它翻译过来,又加了一些自己的见解。方便国内的小伙伴们学习~
为啥要说是‘准零基础‘呢,就是说你需要了解一些基本的信号学和数学知识(至少听说过傅里叶变换,离散数字信号,频域分析这些概念!!),如果你真的是连这些都没听说过,那好吧,这篇文章帮不了你,出门左转祝你成功~
差点忘了~感谢alwatslearn 网站,作者是哪位没找到,不好意思啦。
废话就说到这里啦~ 下面进入正题
//-----------------------------------前言唠叨废话结束----------干货开始---------
想要透彻的掌握FFT,在看code之前,首先要先了解FFT的数学原理,本文先从数学原理开始介绍FFT,然后再来讨论实现FFT的code。
有过一些信号处理方面基础的小伙伴们可能知道,FFT(傅里叶变换)是建立在DFT(离散傅里叶变换)基础上的。FFT 可以说是DFT的另一种版本,是在DFT的基础上更快速,更适合计算机运算的一种傅里叶变换。所以,我们先从DTF开始。
DTF主要实现的功能是将时域的数据转换为频域的数据。DFT意味着对一个无限周期限号进行无限分割。其最基本的公式如 公式1 所示。
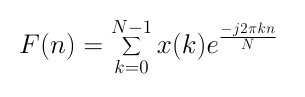 公式1
x(k) 是将要被转换到频域的时域信号(以时间为横轴的波形)
下面是DFT中需要用到的基本概念:
(下列概念可能稍微有些抽象,不好理解,先看一下有些印象,稍后结合例子讲解之后应该就可以理解了)
1. 采样率(sampling rate,sr). 其意义为在一个时间周期内所采样次数。为了学习的简单,我们姑且认为采样 时间间隔(sample interval,si)是相等的。
2. 基础时间(fundamental period,T). 全部采样所需的时间。也称为 窗口(window)。
3. 基础频率 (fundamental frequency,f0). 也就是1/T, 第一个波的频率为f0,第二个播的频率 2*f0,第 三个波的频率为 3*f0,以此类推
4. 采样数量N
5. 奈奎斯特频率fc. fc是依据奈奎斯特采样定律所得出的可以被正确采样的信号的最大频率,如果信号超过这个 频率,那么采样后的信号将会失真。奈奎斯特采样定律是信号理论里最进本的定律(即采样频率至少应为原 信号的两倍),在这里不做过多的讲解,详情可以参阅维基,定律本身十分简单容易理解。
6. 欧拉公式(Euler's formula)
公式1
x(k) 是将要被转换到频域的时域信号(以时间为横轴的波形)
下面是DFT中需要用到的基本概念:
(下列概念可能稍微有些抽象,不好理解,先看一下有些印象,稍后结合例子讲解之后应该就可以理解了)
1. 采样率(sampling rate,sr). 其意义为在一个时间周期内所采样次数。为了学习的简单,我们姑且认为采样 时间间隔(sample interval,si)是相等的。
2. 基础时间(fundamental period,T). 全部采样所需的时间。也称为 窗口(window)。
3. 基础频率 (fundamental frequency,f0). 也就是1/T, 第一个波的频率为f0,第二个播的频率 2*f0,第 三个波的频率为 3*f0,以此类推
4. 采样数量N
5. 奈奎斯特频率fc. fc是依据奈奎斯特采样定律所得出的可以被正确采样的信号的最大频率,如果信号超过这个 频率,那么采样后的信号将会失真。奈奎斯特采样定律是信号理论里最进本的定律(即采样频率至少应为原 信号的两倍),在这里不做过多的讲解,详情可以参阅维基,定律本身十分简单容易理解。
6. 欧拉公式(Euler's formula)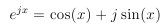 ,复数概念最基本的公式。相信大家都会,详情可参阅维基百科。
7. 将要进行DFT的时域信号,x(t).
8.
,复数概念最基本的公式。相信大家都会,详情可参阅维基百科。
7. 将要进行DFT的时域信号,x(t).
8. 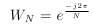 为了让指数表达更简洁,采用Wn 代替。 有些地方也将它称为 twiddle fatctor(旋转因子)。
为了让指数表达更简洁,采用Wn 代替。 有些地方也将它称为 twiddle fatctor(旋转因子)。
了解完基本的定义,下面我们结合一个简单的例子来了解一下DFT 到底是干啥的。 为了简便,我们将对一个正弦信号进行采样,采样点的个数为 N(number of points),然后对其进行DFT。在DFT的过程中上面所介绍的概念将会被用到。在现实生活中,DFT的信号一般远比正弦信号复杂。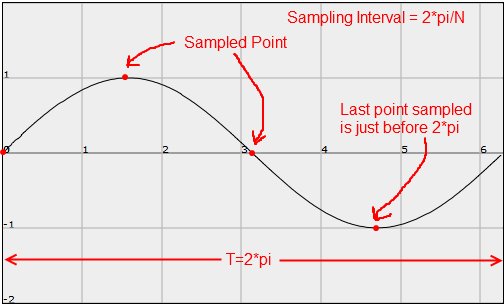 图 1
图 1
如图 1 所示,被采样的信号时一个正弦信号,横轴为时间,纵轴为振幅,红点为采样点(sampled point),基础时间为T,采样间隔(sampling interval)为2*pi/4。 从图可以看出,原始信号可以通过这四个采样点被还原,换句话说虽然只从无限多个点中采了4个点,但是原始正弦信号的属性可以从这四个点中反映出来。 我们还需要知道被采样的这个正弦信号的周期,这样我们就可以计算出频率。在这个例子里,我们周期为T,0.1s。所以我们的所采样的信号频率就是10Hz。一个周期采样四次,所以我们的采样率(sample rate)就是40Hz。 采样后得到的离散信号是: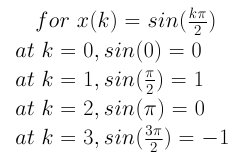 在进行DFT之前,先需要考虑一下旋转因子
在进行DFT之前,先需要考虑一下旋转因子
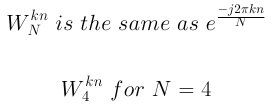 DFT公式,采样四次
DFT公式,采样四次
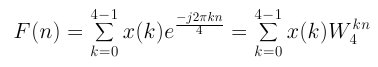 用欧拉公式进行变换
用欧拉公式进行变换
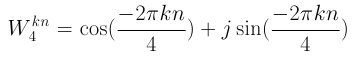 得到的结果:
得到的结果:
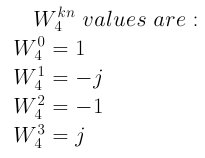 如果k的值继续增加,那么值还是会依照上面的次序循环。例如k=5 w=1, k=6 w=-j···
现在把上面的结果加起来
如果k的值继续增加,那么值还是会依照上面的次序循环。例如k=5 w=1, k=6 w=-j···
现在把上面的结果加起来
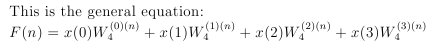 DFT得到四种个不同点的频率
DFT得到四种个不同点的频率
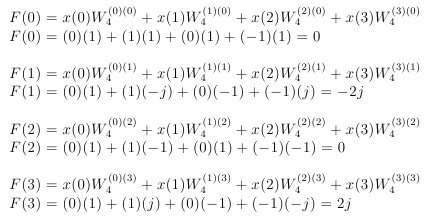 现在来对结果进行一下分析
每一个F(n)的值代表着一段频率的值。每一个采样点的频率为 基础频率*n 。 在这个例子中 基础频率为f0(10 Hz),那么第一个点的频率就是f0*0。 另外需要注意的是,结果的值是一个复数,而复数有两部分组成,实部和虚部;复数的幅值是实部与虚部平方和的开方即“sqrt(real*real+imaginary*imaginary)”
下图(图 2)为我们根据上面的结果画出来的频率频谱图
现在来对结果进行一下分析
每一个F(n)的值代表着一段频率的值。每一个采样点的频率为 基础频率*n 。 在这个例子中 基础频率为f0(10 Hz),那么第一个点的频率就是f0*0。 另外需要注意的是,结果的值是一个复数,而复数有两部分组成,实部和虚部;复数的幅值是实部与虚部平方和的开方即“sqrt(real*real+imaginary*imaginary)”
下图(图 2)为我们根据上面的结果画出来的频率频谱图
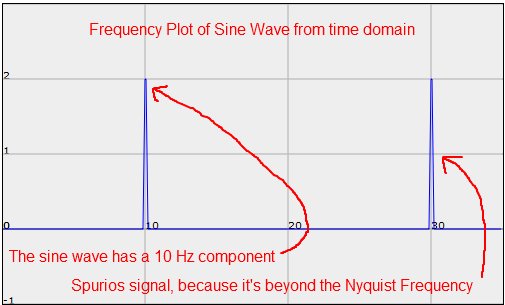 图 2
对比图1和图2可以看出, 图2为频域的图,横轴为频率。从图中可以看到在10Hz处有个一spike(钉子),这与我们的预计相符,因为我们采样的就是一个10Hz的正弦信号。而图中在30Hz处还有一个spike,这是咋回事呢?这里我们之前介绍的奈奎斯特采样定理就要派上用场了,根据采样定理,我们采样频率(saple rate)是40Hz,说以所有大于20Hz的频率都是无效的,所以图中30Hz的spike是无效的。
这里我们用了一个简单的正弦信号做例子,在现实生活中的信号通常会比正弦信号复杂的多,相应的,在其频域中也会有更多的spike例如 图3 所示的三角波。
图 2
对比图1和图2可以看出, 图2为频域的图,横轴为频率。从图中可以看到在10Hz处有个一spike(钉子),这与我们的预计相符,因为我们采样的就是一个10Hz的正弦信号。而图中在30Hz处还有一个spike,这是咋回事呢?这里我们之前介绍的奈奎斯特采样定理就要派上用场了,根据采样定理,我们采样频率(saple rate)是40Hz,说以所有大于20Hz的频率都是无效的,所以图中30Hz的spike是无效的。
这里我们用了一个简单的正弦信号做例子,在现实生活中的信号通常会比正弦信号复杂的多,相应的,在其频域中也会有更多的spike例如 图3 所示的三角波。
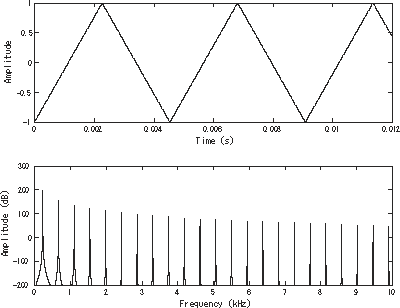 图3
DFT的原理基本就是这些,下一章我们就开始学习FFT喽~
图3
DFT的原理基本就是这些,下一章我们就开始学习FFT喽~
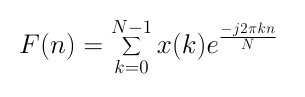 公式1
x(k) 是将要被转换到频域的时域信号(以时间为横轴的波形)
下面是DFT中需要用到的基本概念:
(下列概念可能稍微有些抽象,不好理解,先看一下有些印象,稍后结合例子讲解之后应该就可以理解了)
1. 采样率(sampling rate,sr). 其意义为在一个时间周期内所采样次数。为了学习的简单,我们姑且认为采样 时间间隔(sample interval,si)是相等的。
2. 基础时间(fundamental period,T). 全部采样所需的时间。也称为 窗口(window)。
3. 基础频率 (fundamental frequency,f0). 也就是1/T, 第一个波的频率为f0,第二个播的频率 2*f0,第 三个波的频率为 3*f0,以此类推
4. 采样数量N
5. 奈奎斯特频率fc. fc是依据奈奎斯特采样定律所得出的可以被正确采样的信号的最大频率,如果信号超过这个 频率,那么采样后的信号将会失真。奈奎斯特采样定律是信号理论里最进本的定律(即采样频率至少应为原 信号的两倍),在这里不做过多的讲解,详情可以参阅维基,定律本身十分简单容易理解。
6. 欧拉公式(Euler's formula)
公式1
x(k) 是将要被转换到频域的时域信号(以时间为横轴的波形)
下面是DFT中需要用到的基本概念:
(下列概念可能稍微有些抽象,不好理解,先看一下有些印象,稍后结合例子讲解之后应该就可以理解了)
1. 采样率(sampling rate,sr). 其意义为在一个时间周期内所采样次数。为了学习的简单,我们姑且认为采样 时间间隔(sample interval,si)是相等的。
2. 基础时间(fundamental period,T). 全部采样所需的时间。也称为 窗口(window)。
3. 基础频率 (fundamental frequency,f0). 也就是1/T, 第一个波的频率为f0,第二个播的频率 2*f0,第 三个波的频率为 3*f0,以此类推
4. 采样数量N
5. 奈奎斯特频率fc. fc是依据奈奎斯特采样定律所得出的可以被正确采样的信号的最大频率,如果信号超过这个 频率,那么采样后的信号将会失真。奈奎斯特采样定律是信号理论里最进本的定律(即采样频率至少应为原 信号的两倍),在这里不做过多的讲解,详情可以参阅维基,定律本身十分简单容易理解。
6. 欧拉公式(Euler's formula)了解完基本的定义,下面我们结合一个简单的例子来了解一下DFT 到底是干啥的。 为了简便,我们将对一个正弦信号进行采样,采样点的个数为 N(number of points),然后对其进行DFT。在DFT的过程中上面所介绍的概念将会被用到。在现实生活中,DFT的信号一般远比正弦信号复杂。
 图 1
图 1
如图 1 所示,被采样的信号时一个正弦信号,横轴为时间,纵轴为振幅,红点为采样点(sampled point),基础时间为T,采样间隔(sampling interval)为2*pi/4。 从图可以看出,原始信号可以通过这四个采样点被还原,换句话说虽然只从无限多个点中采了4个点,但是原始正弦信号的属性可以从这四个点中反映出来。 我们还需要知道被采样的这个正弦信号的周期,这样我们就可以计算出频率。在这个例子里,我们周期为T,0.1s。所以我们的所采样的信号频率就是10Hz。一个周期采样四次,所以我们的采样率(sample rate)就是40Hz。 采样后得到的离散信号是:
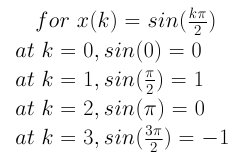 在进行DFT之前,先需要考虑一下旋转因子
在进行DFT之前,先需要考虑一下旋转因子
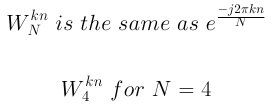 DFT公式,采样四次
DFT公式,采样四次
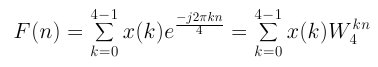 用欧拉公式进行变换
用欧拉公式进行变换
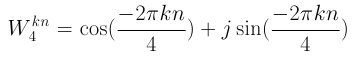 得到的结果:
得到的结果:
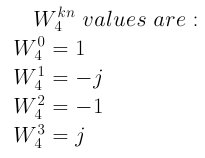 如果k的值继续增加,那么值还是会依照上面的次序循环。例如k=5 w=1, k=6 w=-j···
现在把上面的结果加起来
如果k的值继续增加,那么值还是会依照上面的次序循环。例如k=5 w=1, k=6 w=-j···
现在把上面的结果加起来
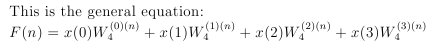 DFT得到四种个不同点的频率
DFT得到四种个不同点的频率
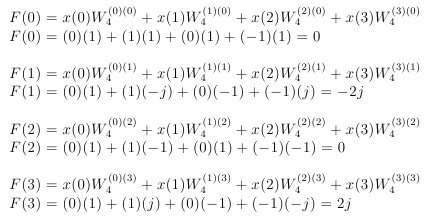 现在来对结果进行一下分析
每一个F(n)的值代表着一段频率的值。每一个采样点的频率为 基础频率*n 。 在这个例子中 基础频率为f0(10 Hz),那么第一个点的频率就是f0*0。 另外需要注意的是,结果的值是一个复数,而复数有两部分组成,实部和虚部;复数的幅值是实部与虚部平方和的开方即“sqrt(real*real+imaginary*imaginary)”
下图(图 2)为我们根据上面的结果画出来的频率频谱图
现在来对结果进行一下分析
每一个F(n)的值代表着一段频率的值。每一个采样点的频率为 基础频率*n 。 在这个例子中 基础频率为f0(10 Hz),那么第一个点的频率就是f0*0。 另外需要注意的是,结果的值是一个复数,而复数有两部分组成,实部和虚部;复数的幅值是实部与虚部平方和的开方即“sqrt(real*real+imaginary*imaginary)”
下图(图 2)为我们根据上面的结果画出来的频率频谱图
 图 2
对比图1和图2可以看出, 图2为频域的图,横轴为频率。从图中可以看到在10Hz处有个一spike(钉子),这与我们的预计相符,因为我们采样的就是一个10Hz的正弦信号。而图中在30Hz处还有一个spike,这是咋回事呢?这里我们之前介绍的奈奎斯特采样定理就要派上用场了,根据采样定理,我们采样频率(saple rate)是40Hz,说以所有大于20Hz的频率都是无效的,所以图中30Hz的spike是无效的。
这里我们用了一个简单的正弦信号做例子,在现实生活中的信号通常会比正弦信号复杂的多,相应的,在其频域中也会有更多的spike例如 图3 所示的三角波。
图 2
对比图1和图2可以看出, 图2为频域的图,横轴为频率。从图中可以看到在10Hz处有个一spike(钉子),这与我们的预计相符,因为我们采样的就是一个10Hz的正弦信号。而图中在30Hz处还有一个spike,这是咋回事呢?这里我们之前介绍的奈奎斯特采样定理就要派上用场了,根据采样定理,我们采样频率(saple rate)是40Hz,说以所有大于20Hz的频率都是无效的,所以图中30Hz的spike是无效的。
这里我们用了一个简单的正弦信号做例子,在现实生活中的信号通常会比正弦信号复杂的多,相应的,在其频域中也会有更多的spike例如 图3 所示的三角波。
 图3
DFT的原理基本就是这些,下一章我们就开始学习FFT喽~
图3
DFT的原理基本就是这些,下一章我们就开始学习FFT喽~