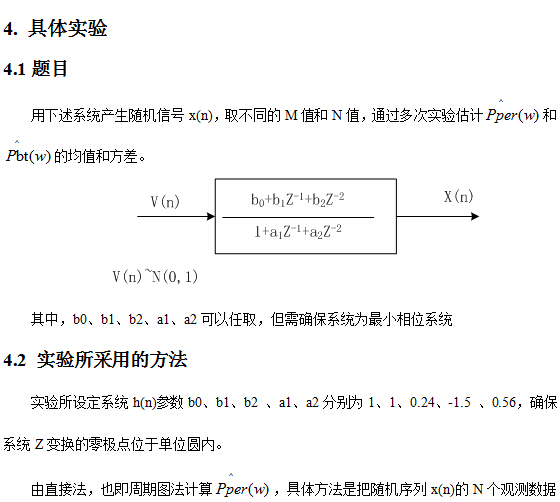
%1、直接法： clc;clear all; u = wgn(1,2000,0); %产生高斯白噪声信号样本点2000个 b = [1 1 0.24]; a = [1 -1.5 0.56]; %滤波器系数 xn = filter(b,a,u) % u通过滤波器的输出xn N = 1000; xn = xn(1,1:N); %取x的1000个样本点分析 nfft=1024; %取1024点fft运算 Perw=abs(fft(xn,nfft)).^2/N; %按公式先计算x(n)的离散傅立叶变换，得X(k)，然后再取其幅值的平方，并除以N t=0:round(nfft/2-1); f=t*N/nfft; Perw_1=10*log10(Perw(t+1)); figure; plot(f,Perw_1); title('直接法功率谱'); xlabel('频率/Hz'); ylabel('功率谱密度'); Mean_Perw = mean(Perw_1); Var_Perw= std(Perw_1); disp(['Perw的均值为：' ,num2str(Mean_Perw)]); disp(['Perw的方差为：' ,num2str(Var_Perw)]); %2、间接法： i = 0; gn = xn; for M =600:200:1000 %M分别取600 800 1000 i = i+1; xn = gn(1,1:M); cxn=xcorr(xn,'unbiased'); %计算序列的自相关函数 CXk=fft(cxn,nfft); Pbt=abs(CXk); index=0:round(nfft/2-1); k=index*M/nfft; figure; plot(k,10*log10(Pbt(index+1))); 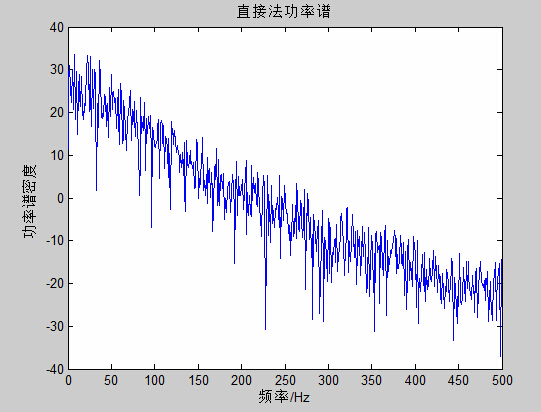title(['间接法（自相关函数法）功率谱','M=',num2str(M)]); xlabel('频率/Hz'); ylabel('功率谱密度'); Mean_Pbtw = mean(10*log10(Pbt(index+1))); Var_Pbtw= std(10*log10(Pbt(index+1))); disp(['Pbtw',num2str(i),'的均值为：' ,num2str(Mean_Pbtw)]); disp(['Pbtw',num2str(i),'的方差为：' ,num2str(Var_Pbtw)]); end %3、AR现代谱估计法： clc;clear all; u = wgn(1,2000,0); %产生高斯白噪声信号样本点2000个 b = [1 1 0.24]; a = [1 -1.5 0.56]; %滤波器系数 xn = filter(b,a,u) % u通过滤波器的输出xn N = 1000; %N同时也表示采样率 xn = xn(1,1:N); %取x的1000个样本点分析 Nfft=1024; %取1024点fft运算 ORDER = 5; [Pxx,W] = pyulear(xn,ORDER,Nfft); t=0:round(Nfft/2-1); f=t*N/Nfft; Pxx_1 = 10*log10(Pxx(t+1)); plot(f,Pxx_1); 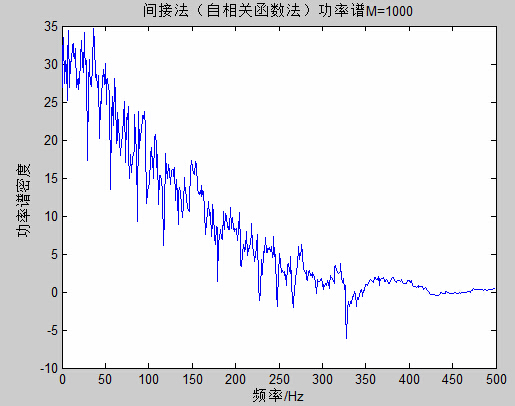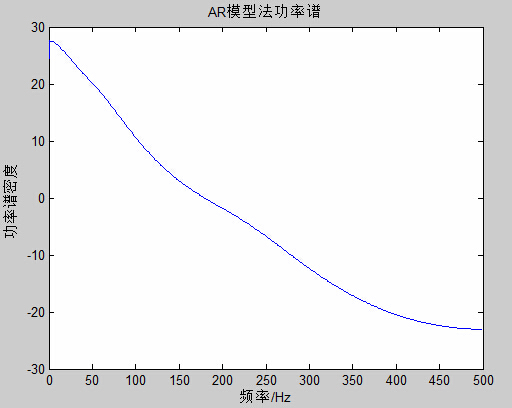title('AR模型法功率谱'); xlabel('频率/Hz'); ylabel('功率谱密度'); Mean_Pxx = mean(Pxx_1); Var_Pxx= std(Pxx_1); disp(['Perw的均值为：' ,num2str(Mean_Pxx)]); disp(['Perw的方差为：' ,num2str(Var_Pxx)]);