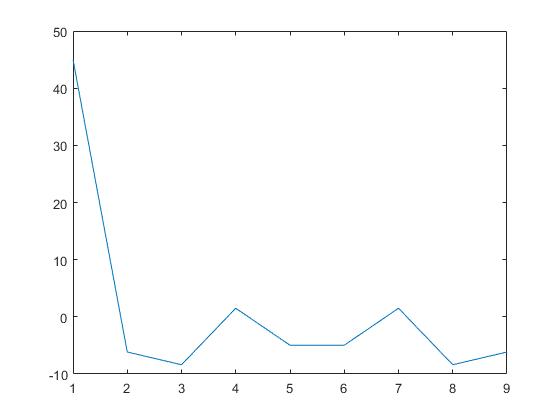
关于卷积的两种手算方法见链接 matlab中fft函数是对序列做DFT，第二个参数是采样点的数量，当缺省时，默认为输入信号序列的长度；当大于信号序列的长度时候，对输入序列后面补零计算，频域信号的分辨率因此而变细，但是这时候的分辨率是伪分辨率。 设定信号序列s1，length（s1） = 9 s1 = [1,7,8,9,5,4,6,3,2] 调用fft函数，对s1进行傅里叶变换 plot(real(fft(s1))) 结果如下 将第二个参数设置成100 figure plot(real(fft(s1,100))) 结果为 通过对比可以看出，补零进行傅里叶变换的结果是频域图形的分辨率变高了，但仍应注意此时候的分辨率是伪分辨率。 因为 DTFT(卷积（s1，s2）) = DTFT（s1，n+m-1）*DTFT（s2,n+m-1），因此想通过Matlab中的fft函数获得线卷积的，可以通过conv 或者 IDFT(DTFT（s1，n+m-1）*DTFT（s2,n+m-1）)两种方法获得。 同时以上的fft(s1,N).*fft(s2,N)也符合循环卷积的频域表现形式，也就是说IDTFT(DTFT(s1)*DTFT(s2)）) 是s1、s2的循环卷积。 因此对于conv（s1，s2） 这种计算量比较大的计算需求，就先补零等价转换成循环卷积 计算，再各自转换到频域相乘以缩减计算量，相乘后通过IDTFT回到时域就是循环卷积的结果，也就是conv（s1，s2）的结果了，当s1、s2的序列越长，计算资源的节省效果就越明显。 PS：通过以上分析也可以看出，通过ifft（fft(s1).*fft(s2)）算出来的不是s1、s2的卷积结果，而是他们的循环卷积结果，要计算卷积结果可以通过conv（s1，s2）进行计算。