1、通过这一实验,能够熟练掌握快速离散傅里叶变换FFT的原理及其用 FFT 进行频谱分析的基本方法。
2、在通过计算机上用软件实现 FFT 及信号的频谱分析。
3、通过实验对离散傅里叶变换的主要性质及 FFT 在数字信号处理中的重要作用有进一步的了解。
- 离散傅里叶变换(DFT)及其主要性质DFT 表示离散信号的离散频谱,DFT 的主要性质中有奇偶对称特性,虚实特性等。通过实验可以加深理解。
DFT 定义:

实序列的 DFT 具有偶对称的实部和奇对称的虚部,即

。
实序列 DFT 的这个特性,在本实验中可以通过实指数序列及三角序列看出来。
对于单一频率的三角序列来说它的 DFT 谱线也是单一的,这个物理意义我们可以从实
验中得到验证。
当周期减小时显然

的谱只应该在k= 3及k = N-3才有分量,实验者可以通过和上述相同的步骤加以理论证明。
由于
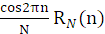
与
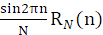
相位差

,所以它的 DFT 只包括实部而没有虚部,以上这些性质可在本实验中得到验证。
2、利用 DFT 对信号进行频谱分析
DFT 的重要应用之一是对时域连续信号的频谱进行分析,称为傅里叶分析,时域连续信号离散傅里叶分析的基本步骤如图所示。
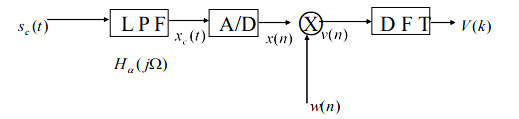
因为DFT频率间隔为
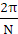
,且模拟频率
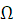
和数字频率

间的关系为
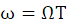
,所以离散的频率函数各频率点对应的模拟频率为:
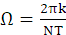
。
显然频率分辨率△f为:
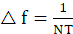
利用DFT计算频谱,只给出频谱
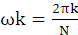
或
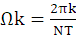
的频率分量,即频率的采样值,而不可能得到连续的频谱函数。
如果在两个离散的谱线之间有一个特别大的频谱分量,就无法检测出来了。
为了在保持原来回频谱形状不变的情况下,使谱线加密,即使频域采样点数增加,从而使原来看不到的频谱分量变得可以看到,可以通过在信号数据的末端补加一些零值点,使DFT 计算周期内点数增加,但又不改变原有的记录数据的方法来实现。
1、实验前学生应认真学习《数字信号处理》中有关章节的内容,掌握快速傅里叶变换的基本原理以及如何用 FFT 等计算信号频谱。
2、编程,上机独立调试,通过程序,并打印出X(k)或
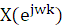
的值,作出|X(k)|或
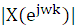
的曲线。
(1) 周期为 N 的正弦序列
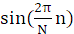
,且
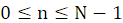
,
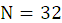
,求N点DFT。
(2) 矩形序列
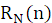
,N=8;求 N 点 DFT 和 2N 点 DFT。
(3) 有一调幅信号xa(t)=[1+cos(2π×100t)]cos(2π×600t)
用 DFT 做频谱分析,要求能分辨xa(t)的所有频率分量,若用fs=3kHz频率抽样,首先分析抽样数据为 N=120 点的频谱分析,求X(k)=DFT[x(n)],N=120点,画出X(k)的幅频特性|X(k)|,标出主要点的坐标值。其次分析抽样数据为 N=128 点的频谱分析,求X(k)=DFT[x(n)],N=128点,画出X(k)的幅频特性|X(k)|,标出主要点的坐标值。比较上述不同长度采样点情况下的实验结果,说明利用 DFT 对连续信号进行傅里叶分析可能造成哪些误差?
1、实验要求及实验内容
2、简述实验原理,列出实验程序清单,并附上必要的程序说明。
3、记录调试运行情况及所遇问题的解决方法。
4、记录实验结果,实验后,对结果进行分析。
思考:利用 DFT 对连续信号进行傅里叶分析可能造成哪些误差?
- 周期为 N 的正弦序列
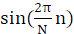 ,且
,且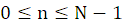 ,
,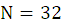 ,求N点DFT。
,求N点DFT。
- 程序清单
%正弦序列DFT
clear all
close all
N=32;
n=0:N-1;
xn=sin(2*pi*n/32);
XK=fft(xn,N);
magXK=abs(XK); %幅频特性
phaXK=angle(XK); %相频特性
k=0:length(magXK)-1;
stem(k,magXK,'.'); %信号幅频特性曲线
xlabel('k');
ylabel('|X(k)|');
title('X(k) N=32')
(2)仿真图像

(3)结果分析
从图像中可以看出,当0≤n≤N-1,N=32时,当且仅当K=1和K=31时,|X(k)|=16,其余点的|X(k)|=0。这是因为:
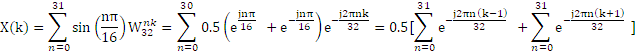
当k-1=0即k=1时,
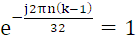
,所以X(k)=0.5×32=16;
同理,当k+1=32即k=31时,
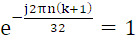
,所以X(k)=0.5×32=16。
2、矩形序列
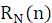
,N=8;求 N 点 DFT 和 2N 点 DFT。
(1)程序清单
%矩形序列DFT
N=8;
x=[ones(1,8),zeros(1,N-8)];
n=0:N-1;
X=dft(x,N);
magX=abs(X);
phaX=angle(X)*180/pi;
k=(0:length(magX)'-1)*N/length(magX);
subplot(2,2,1);
stem(n,x);
ylabel('x(n)');
subplot(2,2,2);
stem(k,magX,'.');
axis([0,10,0,8]); %R8(n)N点幅频曲线图
ylabel('|X(k)| of N=8');
N=16;
x=[ones(1,8),zeros(1,N-8)];
n=0:N-1;
X=dft(x,N);
magX=abs(X);
phaX=angle(X)*180/pi;
k=(0:length(magX)'-1)*N/length(magX);
subplot(2,2,3);
stem(n,x,'.');
ylabel('x(n)');
subplot(2,2,4);
stem(k,magX,'.');
axis([0,15,0,8]); %R8(n)2N点幅频曲线图
ylabel('|X(k)| of N=16');
%%%%%%%%%%%%%%用到的函数:
function[Xk]=dft(xn,N)
n=[0:1:N-1];
k=[0:1:N-1];
WN=exp(-j*2*pi/N);
nk=n'*k;
WNnk=WN.^nk;
Xk=xn*WNnk;
- 仿真图像

- 结果分析
N 点 DFT的幅频曲线图中,0~7这8个点,只有当k=0时|X(k)|不为零,而2N点DFT的幅频曲线则不一样。这是因为,在同一个周期内,2N点的DFT比N点DFT要多取一些点,因此原本N点DFT没有显示的点将在2N点DFT中显示出来。而且,我们可以知道,取的点越多,幅频曲线图将会越精确。
3、有一调幅信号xa(t)=[1+cos(2π×100t)]cos(2π×600t)
用 DFT 做频谱分析,要求能分辨xa(t)的所有频率分量,若用fs=3kHz频率抽样,首先分析抽样数据为 N=120 点的频谱分析,求X(k)=DFT[x(n)],N=120点,画出X(k)的幅频特性|X(k)|,标出主要点的坐标值。其次分析抽样数据为 N=128 点的频谱分析,求X(k)=DFT[x(n)],N=128点,画出X(k)的幅频特性|X(k)|,标出主要点的坐标值。比较上述不同长度采样点情况下的实验结果,说明利用 DFT 对连续信号进行傅里叶分析可能造成哪些误差?
- 程序清单
N3=120;
x3=0:1:N3-1;
%xn3=(1+cos(2*pi*100*x3)).*cos(2*pi*600*x3);
xn3=cos(2*pi*600/3000*x3)+0.5*cos(2*pi*700/3000*x3)+0.5*cos(2*pi*500/3000*x3);
subplot(3,1,1);
plot(x3,xn3);title('xn3');
XK3=fft(xn3,N3);
XK3=abs(XK3);
subplot(3,1,2);
stem(0:length(XK3)-1,XK3,'.');
title('XK3 N=120点DFT');
N30=128;
x30=0:1:N30-1;
%xn30=(1+cos(2*pi*100*x30)).*cos(2*pi*600*x30);
xn30=cos(2*pi*600/3000*x30)+0.5*cos(2*pi*700/3000*x30)+0.5*cos(2*pi*500/3000*x30);
XK30=fft(xn30,2*N30);
XK30=abs(XK30);
subplot(3,1,3);
stem(0:length(XK30)-1,XK30,'.');
title('XK3 N=128点DFT');
- 仿真图像

- 结果分析
主要点的分析:
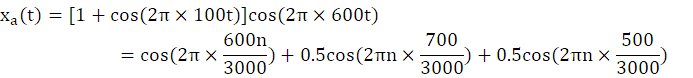
已知
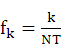
,即
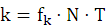
,在此题中,当N=120,fs=3kHz时,
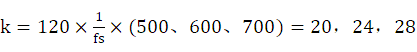
即为三个主要点。又因为|X(k)|图像的对称性,使得92,96,100也为三个主要点。
当N=128时产生了频谱泄露,这是因为:
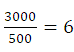
,
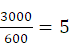
,
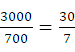
,
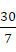
、5、6的最小公倍数是30;当N=120时,
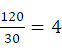
是个整数,而当N=128时,
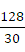
的结果不是整数,即正弦信号不是整数周期,因此产生频谱泄露。
实验报告思考题:在利用 DFT 分析连续信号频谱时,会出现哪些误差?如何克服或减弱?
A.混叠现象: 对于带限连续信号, 只要提高抽样频率使之满足时域抽样定理; 对于非带限信号, 可以根据实际情况对其进行低通滤波, 使之成为带限信号。 工程中的信号一般都不是带限信号, 连续信号在抽样前通常都进过一个低通滤波器 (即抗混叠滤波器) 进行低通滤波,以减少混叠误差,提高频谱分析精度。
B.泄漏现象:在选择矩形窗口的长度时,适当增加窗的长度,可以提高频谱分辨率,但是不能减小旁瓣引起的频谱泄露, 因此可以选择旁瓣幅度很小甚至为零的非矩形窗对信号进行加窗处理,就可以降低频谱泄露。
C.栅栏现象: 改善栅栏现象最常用的方法是在离散序列之后补零, 得到一个比原有序列更长的序列,这样就可以增加频谱图中的很多细节,降低栅栏现象。
通过本次实验,通过这一实验,能够熟练掌握快速离散傅里叶变换(FFT)的原理及其用 FFT 进行频谱分析的基本方法。
 实序列的 DFT 具有偶对称的实部和奇对称的虚部,即
实序列的 DFT 具有偶对称的实部和奇对称的虚部,即 的谱只应该在k= 3及k = N-3才有分量,实验者可以通过和上述相同的步骤加以理论证明。
由于
的谱只应该在k= 3及k = N-3才有分量,实验者可以通过和上述相同的步骤加以理论证明。
由于 因为DFT频率间隔为
因为DFT频率间隔为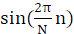 ,且
,且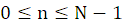 ,
,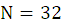 ,求N点DFT。
,求N点DFT。 (3)结果分析
从图像中可以看出,当0≤n≤N-1,N=32时,当且仅当K=1和K=31时,|X(k)|=16,其余点的|X(k)|=0。这是因为:
(3)结果分析
从图像中可以看出,当0≤n≤N-1,N=32时,当且仅当K=1和K=31时,|X(k)|=16,其余点的|X(k)|=0。这是因为:
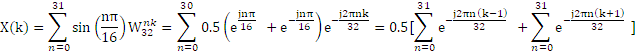 当k-1=0即k=1时,
当k-1=0即k=1时,

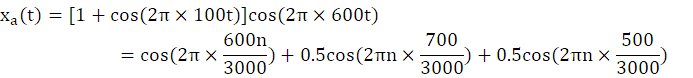 已知
已知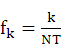 ,即
,即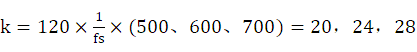 即为三个主要点。又因为|X(k)|图像的对称性,使得92,96,100也为三个主要点。
当N=128时产生了频谱泄露,这是因为:
即为三个主要点。又因为|X(k)|图像的对称性,使得92,96,100也为三个主要点。
当N=128时产生了频谱泄露,这是因为: 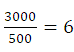 ,
,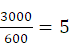 ,
,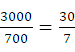 ,
,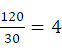 是个整数,而当N=128时,
是个整数,而当N=128时,