图像傅里叶变换的频谱特征

     傅里叶变换在一维信号处理中的地位是显著的，是不可撼动的，然后傅里叶变换在图像处理领域中的应用似乎稍逊一筹，黯然失 {MOD}。究其原因，我想了很久，请允许我用非官方的，不正规的，但却通俗易懂的方式说一下。 一句话概括就是：要化繁为简（DSP），不要弄巧成拙（DIP）。   前半句说的是DFT在信号处理中的应用:      比如说一个音频信号（这里讨论的是数字化后的声音），他在你看来就是一团杂乱无章的信号，你很难直观的感受到他想要表达的意义，而用DFT分析后，很快就能知道其各个频率成分的比重，而且在频域处理起来也非常方便。                      上图中的一个杂乱无章的一维信号经过傅里叶分析后，信号特征一目了然。DFT在一维信号中往往起到了化繁为简的作用。          后半句说的是DFT在图像处理中的应用:      常言道，百闻不如一见，人脑对于图像的理解能力是非常发达的。换句话说，一副图像（不论是灰度的图像还是彩 {MOD}图像）所提供的信息是显而易见，清晰有力的。然而，一副图像的傅里叶频谱图，却常常让人难以理解，捉摸不透，也正因为如此，相对于一维频谱的频域处理方式而言，二维频域的处理方式显得非常有限，例如，二维卷积的频域计算，傅里叶中心切片定理Fourier Slice Theorem（医学领域）。  Matlab代码： I = imresize(im2double(imread('cameraman.tif')),2); figure; imshowpair(I,log(abs(fftshift(fft2(I)))+1),'montage');        我这里再次选用了著名的Cameraman的图像，这幅照片向我们表达的信息是显而易见的，一位优秀的摄影师，黑 {MOD}的风衣，潇洒的发型，很有质感的皮手套，灰 {MOD}的裤子，一台照相机，一个三脚架，草坪，蓝天，背景是MIT。而他的频谱图则并没有像一维的频谱图那样，有助于我们理解图像自身以外的或者是隐藏在图像背后的信息。比如说，中间的那条白线是什么，如果你没看我之前写的那篇文章你可能都不知道它究竟代表了什么。这也就是我为什么说，图像的傅里叶变换有些多此一举，反而把一个简单的问题弄得很复杂，弄巧成拙了。      言归正传，说了这么多，搞图像的哪有不和二维傅里叶变换打交道的呢。现在我就尽力说明一下图像二维傅里叶变换的一些属性（这里主讲二维频谱的特性，一维里面的共有特性就不细讲了）。  

1，周期性

DFT的周期性：时时刻刻都要记住，对于DFT而言，他的空域和频域始终都是沿着X和Y方向无限周期拓展的。 Matlab代码：  % Periodic I = imresize(im2double(imread('cameraman.tif')),2); Iperiodic = repmat(I,3,3); figure; imshowpair(Iperiodic,repmat((log(abs(fftshift(fft2(I)))+1)), 3, 3),'montage'); 如果只取其中的一个周期，则我们会得到如下的结果（即，频谱未中心化）。   为了便于频域的滤波和频谱的分析，常常在变换之前进行频谱的中心化。   附：频谱的中心化      从数学上说是在变换之前用指数项乘以原始函数，又因为e^jπ = 1，所以往往我们在写程序的时候实际上是把原始矩阵乘以（-1）^(x+y)达到频谱居中的目的。如下图所示：1<----->3 对调，2<----->4 对调，matlab中的fftshit命令就是这么干的。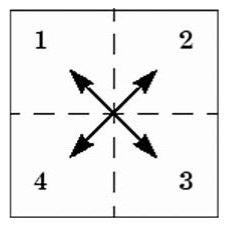 变换后对调频谱的四个象限（swap quadrant） Matlab代码：  I = imresize(im2double(imread('cameraman.tif')),2); figure; imshowpair(log(abs((fft2(I)))+1),log(abs(fftshift(fft2(I)))+1),'montage'); 经过中心化后的频谱 截取了其中的一个周期，作为图像的频谱
   

2，高低频率的分布

      除了周期性之外，还应该知道的就是哪里是高频哪里是低频。在经过频谱居中后的频谱中，中间最亮的点是最低频率，属于直流分量（DC分量）。越往边外走，频率越高。所以，频谱图中的四个角和X,Y轴的尽头都是高频。   没有经过频谱居中处理的频谱图则正好相反，中间区域是高频，而四个角则是DC低频分量。   这里我再用一个正弦波的例子来展示频谱图的高低频的分布，见下图。(下图中，中高频的图像出现了混叠) 频谱中心化以后，正弦波的频点靠中心越近，频率越低，离中心越远，频率越高。 Matlab代码：  % Length of signal L = 512; % Sampling frequency FsLow = 150; FsMid = 500; FsHigh = 1000; % Form sampling vectors IndexLow = linspace(0,FsLow,L); IndexMid = linspace(0,FsMid,L); IndexHigh = linspace(0,FsHigh,L); % build 1D sinewave SineLow = sin(IndexLow); SineMid = sin(IndexMid); SineHigh = sin(IndexHigh); % translate 1D wave into 2D sinewave SinewaveL = repmat(SineLow,[L,1]); SinewaveM = repmat(SineMid,[L,1]); SinewaveH = repmat(SineHigh,[L,1]); % Window function Window = hanning(L)*hanning(L)'; SinewaveLwindowed = SinewaveL.*Window; SinewaveMwindowed = SinewaveM.*Window; SinewaveHwindowed = SinewaveH.*Window; figure; subplot(2,3,1),imshow(SinewaveL,[]),title('Low-freq. sinewave'), subplot(2,3,2),imshow(SinewaveM,[]),title('Med-freq. sinewave'), subplot(2,3,3),imshow(SinewaveH,[]),title('Hig-freq. sinewave'), subplot(2,3,4),imshow(log(abs(fftshift(fft2(SinewaveLwindowed)))+1),[]),title('Spectrum of Low-freq. sinewave'), subplot(2,3,5),imshow(log(abs(fftshift(fft2(SinewaveMwindowed)))+1),[]),title('Spectrum of Med-freq. sinewave'), subplot(2,3,6),imshow(log(abs(fftshift(fft2(SinewaveHwindowed)))+1),[]),title('Spectrum of Hig-freq. sinewave');

 

 

3，频谱图的能量分布

     这里我顺便提一下频谱中的能级分布，则如下图所示。明显，DC分量所占能量最大最多，不论是二维还是一维都应该是这样。频率越高的部分，能量越少。如下图所示，图示画的不好，勉强能够理解就好。中间最小的那个圆圈内包含了大约85%的能量，中间那个圈包含了大约93%的能量，而最外面那个圈则包含了几乎99%的能量。  

 

4，变化方向的一致性

     在二维傅里叶变换中，空间域中横向的周期变化会反应在频谱图中的横轴上，而空间域中纵向的周期变化会反应在频谱图中的纵轴上。空间域中东南方向的周期变化会反应在频谱图中的东北方向，反之亦然。说明见下图。   Matlab代码： % black&white Isize = 512; Iblackwhite = zeros(Isize); Iblackwhite(1:Isize/2,:) = 1; figure; imshowpair(Iblackwhite,log(abs(fftshift(fft2(Iblackwhite)))+1),'montage'); Iwhiteblack = zeros(Isize); Iwhiteblack(:,Isize/2:end) = 1; figure; imshowpair(Iwhiteblack,log(abs(fftshift(fft2(Iwhiteblack)))+1),'montage'); % black&white triangle Hanning = hanning(Isize)*hanning(Isize)'; ItriangleUpper = triu(ones(Isize),0); ItriangleUpper = ItriangleUpper.*Hanning; figure; imshowpair(ItriangleUpper,log(abs(fftshift(fft2(ItriangleUpper)))+1),'montage'); % ItriangleLower = tril(ones(Isize),0); % ItriangleLower = ItriangleLower.*Hanning; % figure; % imshowpair(ItriangleLower,log(abs(fftshift(fft2(ItriangleLower)))+1),'montage'); % flip the upper triangle matrix ItriangleUpperMirror = fliplr(triu(ones(Isize),0)); ItriangleUpperMirror = ItriangleUpperMirror.*Hanning; figure; imshowpair(ItriangleUpperMirror,log(abs(fftshift(fft2(ItriangleUpperMirror)))+1),'montage');   最后再附加一个例子。 Matlab代码：  % form horizontal and vertical sinewaves SineHorz = SinewaveM; SineVert = rot90(SineHorz,1); SineHorzwindowed = SineHorz.*Window; SineVertwindowed = SineVert.*Window; figure; subplot(2,2,1),imshow(SineHorz,[]),title('Vertical sinewave'), subplot(2,2,2),imshow(SineVert,[]),title('Horizontal sinewave'), subplot(2,2,3),imshow(log(abs(fftshift(fft2(SineHorzwindowed)))+1),'InitialMagnification','fit'),title('Spectrum of Vertical sinewave'), subplot(2,2,4),imshow(log(abs(fftshift(fft2(SineVertwindowed)))+1),'InitialMagnification','fit'),title('Spectrum of Horizontal sinewave'),   我在用MATLAB仿真的过程中，为了让频谱更集中，更加有助于理解，我反复的用到了加窗，关于图像的加窗，请看我的另一篇文章：https://blog.csdn.net/daduzimama/article/details/80079215 （全文完） (本文中的所有错误已于：2018年11月1日更正，谢谢大家提出的宝贵意见。) （本文在2019年2月13日，进行了第二次更正，修改了一些重要错误。）   鸣谢： 【1】Matlab 2018b 【2】[Steven W. Smith] The Scientist and Engineer's Guide to Digital Signal Processing (1999) 【3】耐心阅读并提出宝贵意见的读者：qq_34740116，DeepSpace2000。 谢谢收看！ 再见！ 未完待续。。。   《圣经》 马太福音 24章12-13节  -------  只因不法的事增多，许多人的爱心才渐渐冷淡了。 惟有忍耐到底的，必然得救。                                                                                     *配图和本文无关*