一开始的想法就是cos,sin,atan2都可以使用泰勒级数,sqrt可以使用牛顿法。
然后。。。上网找资料。。。
首先是SQRT,这位仁兄基本思路和我一样,但是他在最后提供的这段代码的确很神奇。列在下面。
[cpp]
view plain
copy
print?
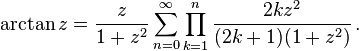 但是感觉收敛效果仍旧一般,所以最终选择了积分式,代码如下:
[cpp]
view plain
copy
print?
但是感觉收敛效果仍旧一般,所以最终选择了积分式,代码如下:
[cpp]
view plain
copy
print?
后面一大段if else条件判断是因为atan2和atan的区别:
 这个方法虽然误差已经很小了,至少不影响我计算方向场,但是应该还有更好的。至少我在stackoverflow里面看到的是如此。比如有如此开源代码,苹果的。
http://blog.csdn.net/simitwsnyx/article/details/45890281
这个方法虽然误差已经很小了,至少不影响我计算方向场,但是应该还有更好的。至少我在stackoverflow里面看到的是如此。比如有如此开源代码,苹果的。
http://blog.csdn.net/simitwsnyx/article/details/45890281
- float Sqrt(float x)
- {
- float xhalf = 0.5f*x;
- int i = *(int*)&x;
- i = 0x5f375a86 - (i >> 1);
- x = *(float*)&i;
- x = x*(1.5f - xhalf*x*x);
- x = x*(1.5f - xhalf*x*x);
- x = x*(1.5f - xhalf*x*x);
- return 1 / x;
- }
- float Sin(float x)
- {
- int sign = 1;
- int itemCnt = 4;
- int k = 0;
- float result = 0.0f;
- float tx = 0.0f;
- int factorial = 1;
- if(x < 0)
- {
- x = -x;
- sign *= -1;
- }
- while(x >= SL_2PI)
- {
- x -= SL_2PI;
- }
- if(x > SL_PI)
- {
- x -= SL_PI;
- sign *= -1;
- }
- if(x > SL_PI_DIV_2)
- {
- x = SL_PI - x;
- }
- tx = x;
- for (k = 0; k < itemCnt; k ++)
- {
- if(k%2 == 0)
- {
- result += (tx / factorial);
- }
- else
- {
- result -= (tx / factorial);
- }
- tx *= (x * x);
- factorial *= (2*(k+1));
- factorial *= (2*(k+1) + 1);
- }
- if (1 == sign)
- return result;
- else
- return -result;
- }
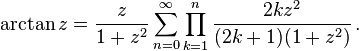 但是感觉收敛效果仍旧一般,所以最终选择了积分式,代码如下:
[cpp]
view plain
copy
print?
但是感觉收敛效果仍旧一般,所以最终选择了积分式,代码如下:
[cpp]
view plain
copy
print?
- float Atan2(float y, float x, int infNum)
- {
- int i;
- float z = y / x, sum = 0.0f,temp;
- float del = z / infNum;
- for (i = 0; i < infNum;i++)
- {
- z = i*del;
- temp = 1 / (z*z + 1) * del;
- sum += temp;
- }
- if (x>0)
- {
- return sum;
- }
- else if (y >= 0 && x < 0)
- {
- return sum + PI;
- }
- else if (y < 0 && x < 0)
- {
- return sum - PI;
- }
- else if (y > 0 && x == 0)
- {
- return PI / 2;
- }
- else if (y < 0 && x == 0)
- {
- return -1 * PI / 2;
- }
- else
- {
- return 0;
- }
- }
后面一大段if else条件判断是因为atan2和atan的区别:
 这个方法虽然误差已经很小了,至少不影响我计算方向场,但是应该还有更好的。至少我在stackoverflow里面看到的是如此。比如有如此开源代码,苹果的。
http://blog.csdn.net/simitwsnyx/article/details/45890281
这个方法虽然误差已经很小了,至少不影响我计算方向场,但是应该还有更好的。至少我在stackoverflow里面看到的是如此。比如有如此开源代码,苹果的。
http://blog.csdn.net/simitwsnyx/article/details/45890281