这是网上的一篇文章, 我重新读了一下, 然后做了一些整理 1.为什么要进行变换
空间图像数据通常是很难压缩的：相邻的采样点具有很强的相关性（相互关联的），而且能量一般平均分布在一幅图像中，从而要想丢掉某些数据和降低数据精度而不明显影响图像质量，就要选择合适的变换，方法，使图像易于被压缩。适合压缩的变换方法要有这样几个性质：
(1).可以聚集图像的能量（将能量集中到少数有意义的数值上）,如下图：

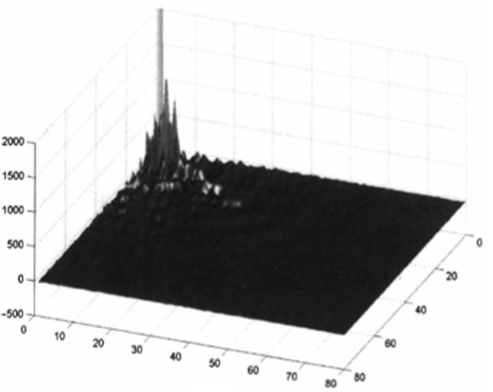
举个例子说明, 左图是变换前的数据, 右图是变换后的数据：

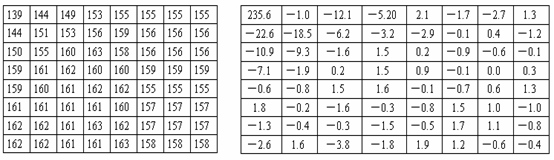
可以看出，经变换后，数据的能量基本上集中到左上方（低频信号）了，而变换后的数据完全可以通过反变换还原成原来的数据。为了达到压缩文件的目的，我们就可以丢弃掉一些能量低的数据（高频信号），而对图像质量影响很小。

1. 可以除去数据之间的相关性（以使丢掉不重要的数据对图像的质量影响很少）。
   
2. 变换方法应该适合用软硬件实现。
   

2.具体变换过程
4x4的DCT变换矩阵如下:

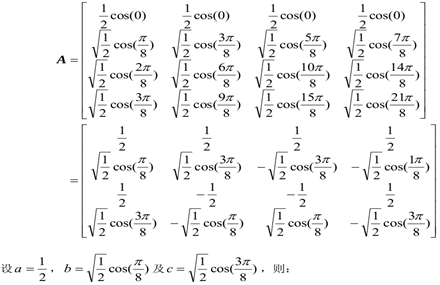
这样我们就得到了,如下矩阵:

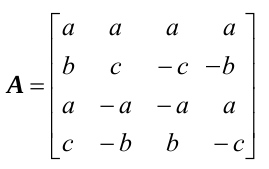
进行推导得到如下:

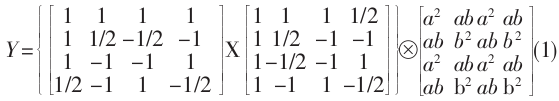
在上式中, 虽然乘以 1/2 的操作可以用右移来实现 , 但这样会产生截断误差 . 因此, 将1/2提到矩阵外面, 并与右边的点乘合并, 进而得到如下的算式:

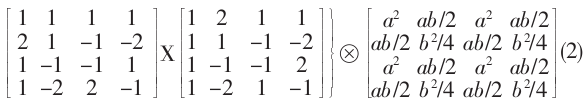
在JM编码器中，变换过程只包括了

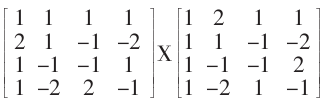
后面的点乘实际上是在量化过程中进行，因为后面的点乘还有实数运算，实数运算将不可避免地产生精度误差,而且运算量巨大。而量化本身就会丢失一些信号，因些，这些实数运算放在量化过程中将大大的降低变换的运算率同时又不明显影响精度？

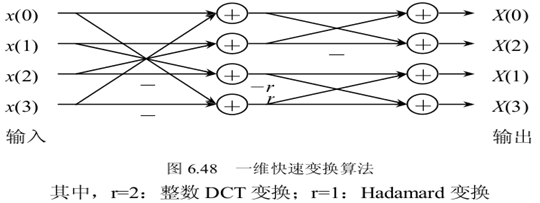
然而，4X4的矩阵运算如果按常规算法的话仍要进行64次乘法运算和48次加法，这将耗费较多的时间，于是在H.264中，有一种改进的 算法（蝶形算法）可以减少运算的次数。这种矩阵运算算法构造非常巧妙，利用构造的矩阵的整数性质和对称性，可完全将乘法运算转化为加法运算.
这里来分析一下蝶形算法，这个蝶形算法和一般FFT的蝶形算法不同，由于我没有找到相关论文，能找到的书和网络资料又语焉不详，只好自己推导。上面的JM代码就是计算下面三个4x4矩阵的过程。
分析一下前两个矩阵的乘法，只分析他们结果矩阵的第一列。有什么办法可以减少运算量呢？首先采用传统方法计算，得到结果：
X[0] = x[00]+x[10]+x[20]+x[30]
X[1] = 2*x[00]+x[10]-x[20]-2*x[30]
X[2]= x[00]-x[10]-x[20]+x[30]
X[3] = x[00]-2x[10]+2x[20]-x[30]
计算代价是16次乘法12次加法，考虑到矩阵的1的乘法可以省略，去除8个乘1，还需要8次乘法和12次加法。那么我们再仔细思考他们的相 关性，从一般算法意义上来说，可以用空间代价换时间代价，比如设置中间变量来减少计算次数。用不同的颜 {MOD}把需要重复运算的部分标上，作为中间变量。
X[0] = x[00]+x[10]+x[20]+x[30]
X[1] = 2*x[00]+x[10]-x[20]-2*x[30]
X[2]= x[00]-x[10]-x[20]+x[30]
X[3] = x[00]-2x[10]+2x[20]-x[30]
那么提取出来的中间变量将是：
x[00]+x[30]
x[00]-x[30]
x[10]+x[20]
x[10]-x[20]
存储了这四个中间变量，我们对比看看蝶形图，和图中第一层的算式相符合。用这些中间变量来组合，就可以把最终的X[0]..X[3], 计算出来。这样，就把运算量降低到2个乘法和8个加法，剩余的运算就是叠代这个算法。
所以，可以得出以下结论：

1. 这个蝶形图和一般意义的FFT或FDCT蝶形图不同，是对H.264在整数DCT基础上的具体算法优化，只对于以上Cf矩阵。
   
2. 计算过程是把上面的三个4x4矩阵乘法分成两两矩阵相乘。再把残差矩阵和后来的中间结果Cf x X一行行分别输入蝶形图进行一维整数DCT计算。
   
3. 蝶形图优化思想就是提取矩阵的相关部分，定义中间变量，减少运算次数。
   

在JM8.6代码中这个碟形算法, 出现的地方很多, 只要牵扯到变换, 就有这种算法. 包括Hadamard变换. 在多个函数中出现, 其实现是一样的.
 
 H.264中DCT变换中所使用的蝶形算法
然而，4X4的矩阵运算如 果按常规算法的话仍要进行64次乘法运算和48次加法，这将耗费较多的时间，于是在H.264中，有一种改进的算法（蝶形算法）可以减少运算的次数。这种 矩阵运算算法构造非常巧妙，利用构造的矩阵的整数性质和对称性，可完全将乘法运算转化为加法运算。

 
     
    
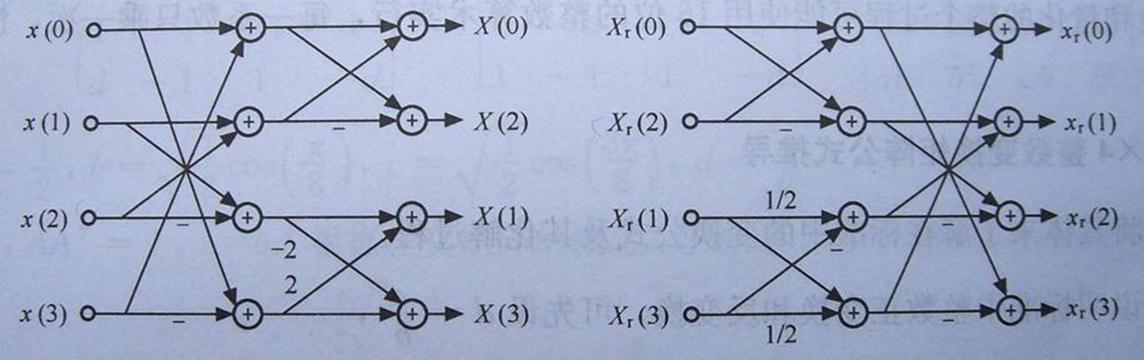
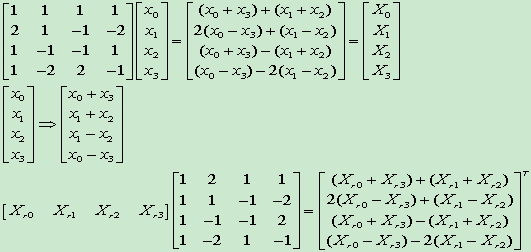
变换过程在JM中代码实现如下：
// Horizontal transform水平变换，其实就是左乘Cf,
for (j=0; j < BLOCK_SIZE && !lossless_qpprime; j++)
{
    for (i=0; i < 2; i++)
{
i1=3-i;
m5[i]=img->m7[i][j]+img->m7[i1][j];
m5[i1]=img->m7[i][j]-img->m7[i1][j];
}
img->m7[0][j]=(m5[0]+m5[1]);
img->m7[2][j]=(m5[0]-m5[1]);
img->m7[1][j]=m5[3]2+m5[2];
img->m7[3][j]=m5[3]-m5[2]2;
}

// Vertical transform垂直变换，其实就是右乘CfT
for (i=0; i < BLOCK_SIZE && !lossless_qpprime; i++)
{
    for (j=0; j < 2; j++)
{
j1=3-j;
m5[j]=img->m7[i][j]+img->m7[i][j1];
m5[j1]=img->m7[i][j]-img->m7[i][j1];
}
img->m7[i][0]=(m5[0]+m5[1]);
img->m7[i][2]=(m5[0]-m5[1]);
img->m7[i][1]=m5[3]2+m5[2];
img->m7[i][3]=m5[3]-m5[2]2;

}