高频电压信号注入框图如下:
 注入的高频电压信号为两相对称正弦高频信号,该信号选取有两点需要注意:
注入的高频电压信号为两相对称正弦高频信号,该信号选取有两点需要注意:
 表示成矢量形式如下:
表示成矢量形式如下:
 这下能看出来了吧,这个电流由两部分组成,一个正序分量和负序分量,正序分量一看就没啥用,看,连位置角都没,没用就把它干掉吧,将α-β
这下能看出来了吧,这个电流由两部分组成,一个正序分量和负序分量,正序分量一看就没啥用,看,连位置角都没,没用就把它干掉吧,将α-β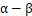 坐标系下的电流乘以旋转因子e-jwt
坐标系下的电流乘以旋转因子e-jwt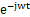 ,搞定,正序变成直流量,负序的旋转频率更高了,没事,多多益善,o,抱歉,忘了一个环节,α-β
,搞定,正序变成直流量,负序的旋转频率更高了,没事,多多益善,o,抱歉,忘了一个环节,α-β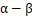 坐标系下的电流也是需要通过滤波搞出来的,滤波器需要滤除高频的PWM频率和低频的电机基频,怎么搞,用带通,好了,言归正传,乘以旋转因子后的信号通过一个高通滤波器,这下爽了,正序全军覆没,剩下的就是i2ej(2θ-2ωt+π2)
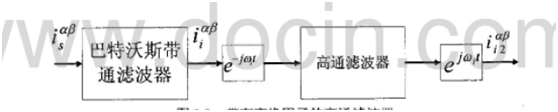
坐标系下的电流也是需要通过滤波搞出来的,滤波器需要滤除高频的PWM频率和低频的电机基频,怎么搞,用带通,好了,言归正传,乘以旋转因子后的信号通过一个高通滤波器,这下爽了,正序全军覆没,剩下的就是i2ej(2θ-2ωt+π2)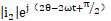 ,下来搞这个,将剩下的信号再乘以旋转因子ejwt
,下来搞这个,将剩下的信号再乘以旋转因子ejwt ,就得到了一个单独的负序分量了,
框图如下:
,就得到了一个单独的负序分量了,
框图如下:
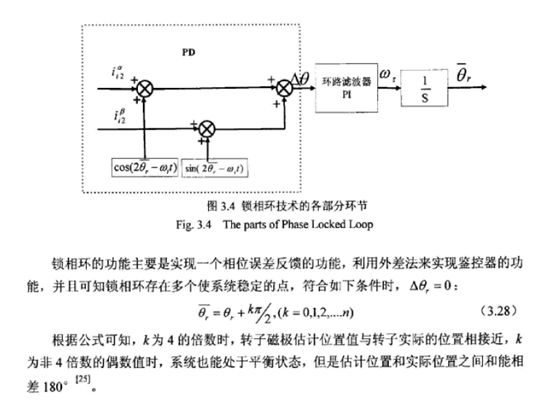
 接下来是作者写的外差发,反正感觉很巧妙,获得误差角
接下来是作者写的外差发,反正感觉很巧妙,获得误差角
 接下来可以用一个PLL锁相环就可以获得角度了,但是由于滤波器的存在,会出现滞后,因此需要进行相位补偿,
接下来可以用一个PLL锁相环就可以获得角度了,但是由于滤波器的存在,会出现滞后,因此需要进行相位补偿,

 额,到此结束,最后PLL之后还需要判断磁极的方向,根据这个K进行判断了。
整体算法框图:
额,到此结束,最后PLL之后还需要判断磁极的方向,根据这个K进行判断了。
整体算法框图:
 以上的理论分析是基于论文 《 高频电压信号注入法PMSM无传感器矢量控制》,原著比较权威哈
以上的理论分析是基于论文 《 高频电压信号注入法PMSM无传感器矢量控制》,原著比较权威哈
 注入的高频电压信号为两相对称正弦高频信号,该信号选取有两点需要注意:
注入的高频电压信号为两相对称正弦高频信号,该信号选取有两点需要注意:
- 信号的频率
- 电机基频一般在200hz以内,因此通常注入的频率要大于这个值,后期可以通过一个高频滤波器将基频干掉。
- IPM开关管一般都是在10khz和20khz的,这个频率高是有很多优点的,比如减小电机扭矩波动,合成的电压矢量更接近与圈,额,想起来美滋滋,但也不能过大,管子受不了的,还有会发热严重,产生高频干扰,10-20K足矣,注入的高频信号要小于这个频率,这样后期搞一个低通就可以把这个频率干掉,美滋滋。
- 信号的幅值
- 一方面单片机的检测精度,估计这个一般问题不大,现在这单片机ADC精度都杠杠滴,说这一点就是担心加的幅值太小,检测不到,这样就尴尬了
- 当然了,也不能过大,过大的话会产生扭矩波动,电机估计要跳舞了,耦合的电流矢量是一个椭圆形的,下面会讲解,一般选择赋值不超过基波电压的10%。
 表示成矢量形式如下:
表示成矢量形式如下:
 这下能看出来了吧,这个电流由两部分组成,一个正序分量和负序分量,正序分量一看就没啥用,看,连位置角都没,没用就把它干掉吧,将α-β
这下能看出来了吧,这个电流由两部分组成,一个正序分量和负序分量,正序分量一看就没啥用,看,连位置角都没,没用就把它干掉吧,将α-β 接下来是作者写的外差发,反正感觉很巧妙,获得误差角
接下来是作者写的外差发,反正感觉很巧妙,获得误差角
 接下来可以用一个PLL锁相环就可以获得角度了,但是由于滤波器的存在,会出现滞后,因此需要进行相位补偿,
接下来可以用一个PLL锁相环就可以获得角度了,但是由于滤波器的存在,会出现滞后,因此需要进行相位补偿,

 额,到此结束,最后PLL之后还需要判断磁极的方向,根据这个K进行判断了。
整体算法框图:
额,到此结束,最后PLL之后还需要判断磁极的方向,根据这个K进行判断了。
整体算法框图:
 以上的理论分析是基于论文 《 高频电压信号注入法PMSM无传感器矢量控制》,原著比较权威哈
以上的理论分析是基于论文 《 高频电压信号注入法PMSM无传感器矢量控制》,原著比较权威哈