原文转载于:http://blog.csdn.net/hj199404182515/article/details/52613969
非常感谢。
关于自适应LMS的理论基础已经非常的成熟,随便找一本关于自适应滤波器的书就会有介绍相关的内容,有的还可出了它的具体算法,但是还没有一本书有讲过怎样编写能够时实(Real Time)处理的基于C的自适应LMS算法(至少我没有见过),而这个应该说是将算法用于时实处理最为关键的一步,本次我就给大家分享一下关于我是如何用C语言来实现时实自适应LMS算法的。
说到时实处理,如果有自己写过时实FIR或者IIR滤波器程序的,可能对时实处理比较的熟悉,那么什么是时实处理呢?怎样来实现时实处理呢?
LMS.c文件
运行的处理器是TMS320C6678 DSP,下面将给出在上面运行的结果。
实验的类型是信号增强,信号的类型和Matlab上的一样以便做对比。程序中调用了dsplib.h中的向量点乘运算函数,如果不是在DSP上或者没有DSPlib的可以自己编写该函数,也不难。
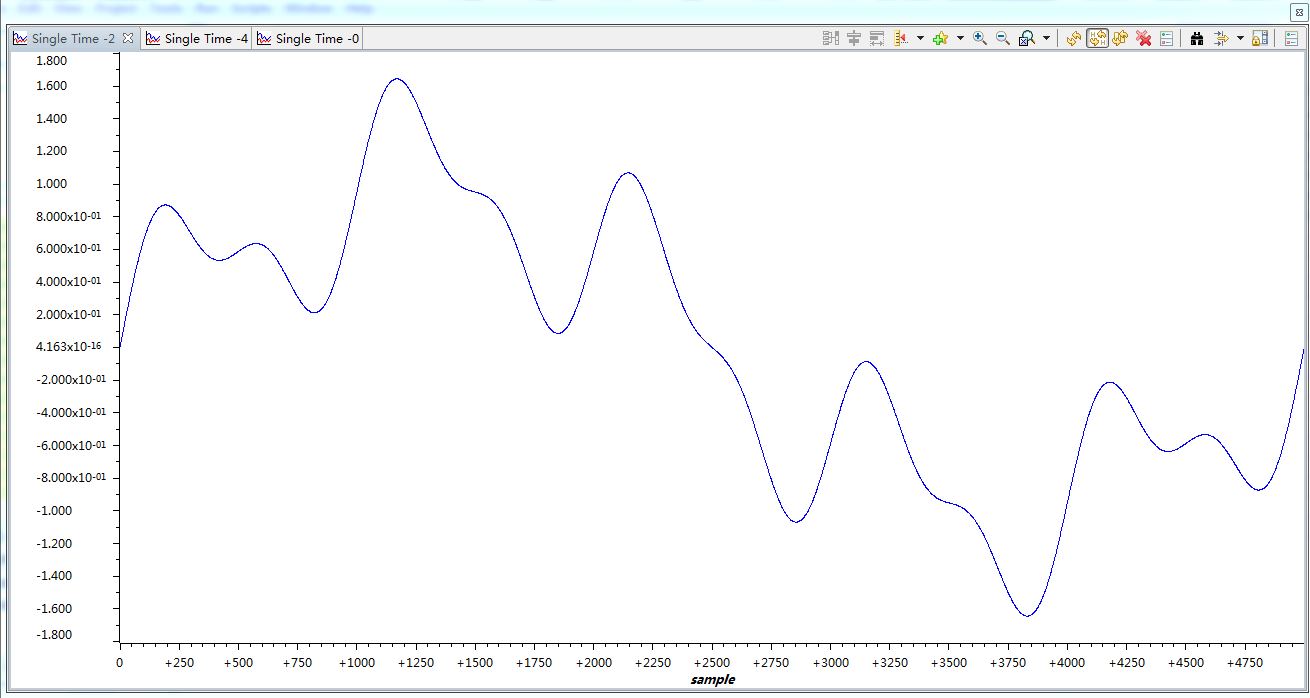
该图显示的是产生的仿真信号
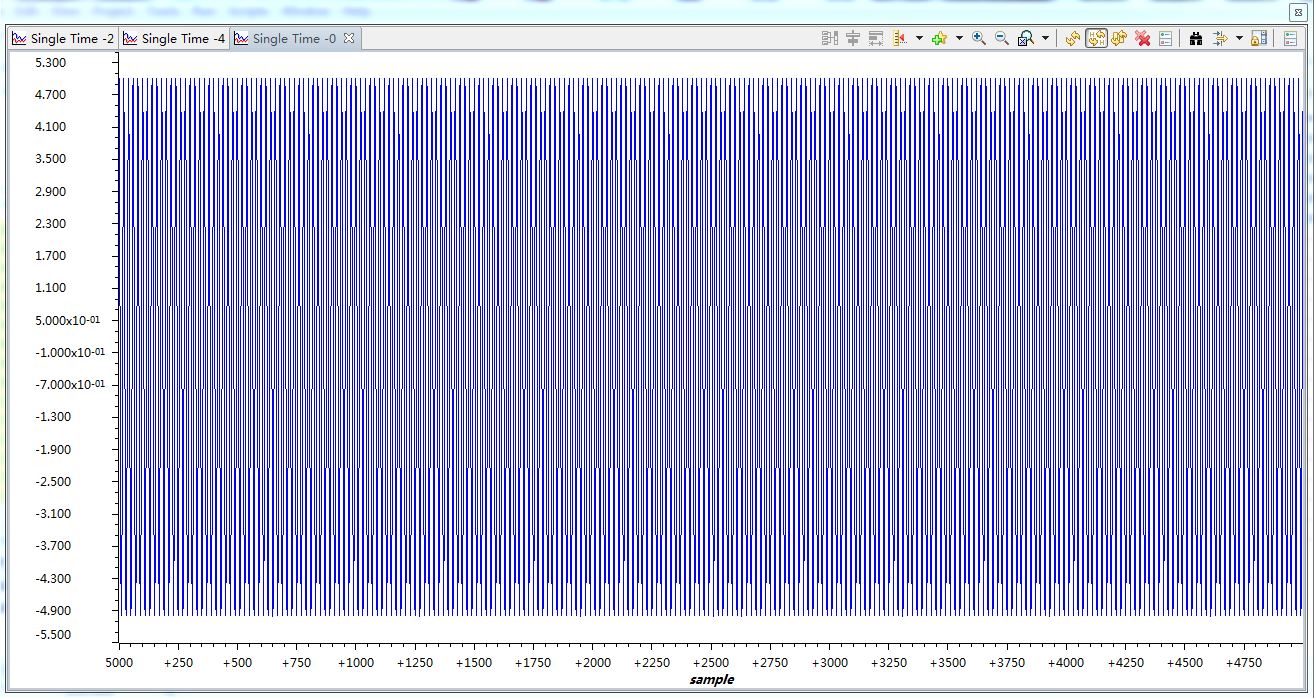
该图显示的是产生的噪声也即干扰
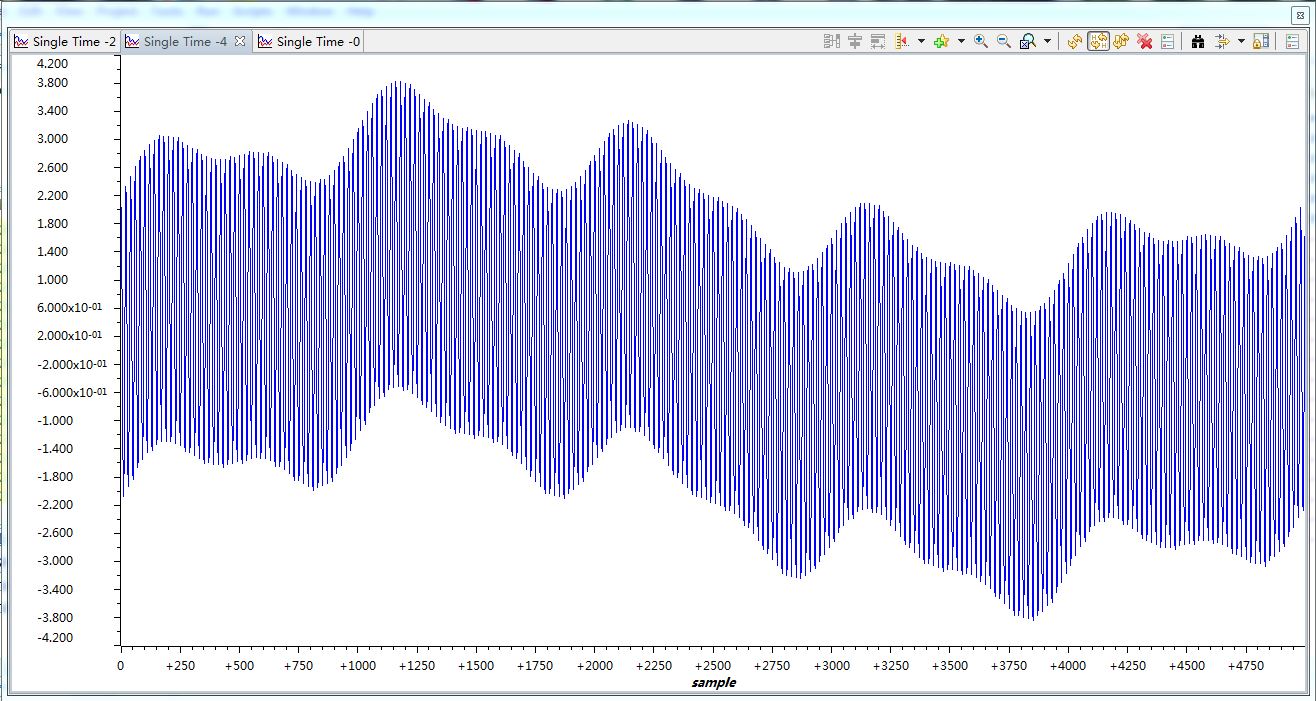
该图是将得到的噪声通过一个线性系统后和信号相加后得到的图形
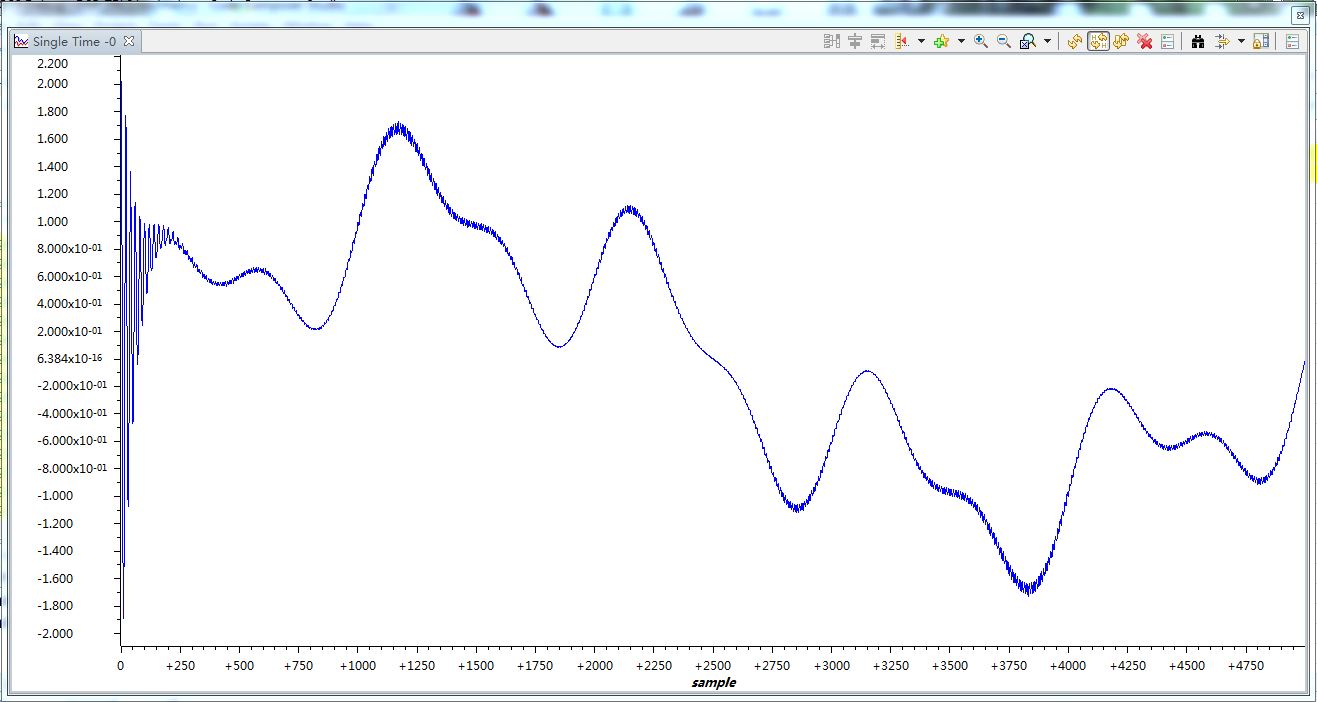
该图是滤波器输出的误差(因为做的是信号的增强,所以我们感兴趣的信号是输出的误差)
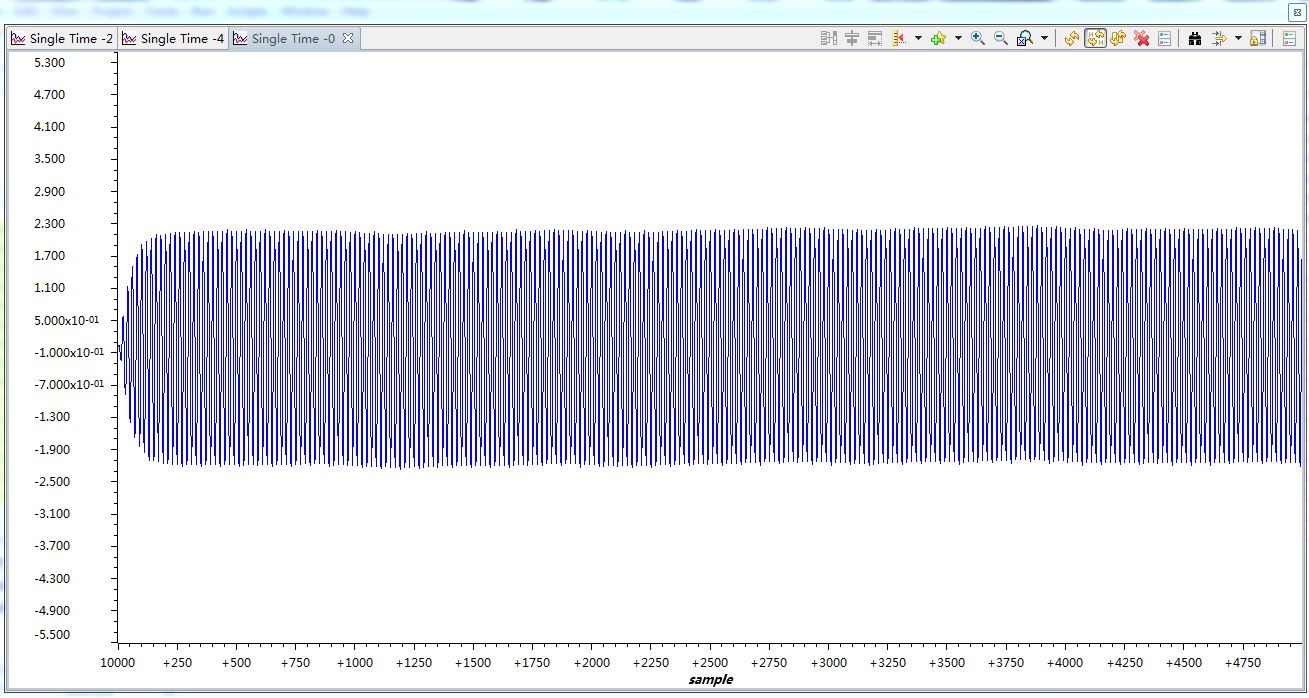
该图是滤波器的输出
可以和Matlab仿真的结果进行对比,会发现它们有一些不同但差别不是很大,主要原因是运算的精度不同,在Matlab上是double float 型的,在6678上的是single float型的。
说到时实处理,如果有自己写过时实FIR或者IIR滤波器程序的,可能对时实处理比较的熟悉,那么什么是时实处理呢?怎样来实现时实处理呢?
什么是实时处理?
简单来说,就是一个处理单元(一段程序代码)在某一时刻得到了输入的数据,然后立即处理得到的数据,并把要输出的数据送入输出单元进行输出,这样就完成了一次时实处理,然后等待下一时刻输入数据,然后重复上述过程。可以看到上述过程是“即刻采集即刻处理”,这就叫时实处理。而非时实处理就是先采集整个时间段的数据,采集完成后再进行处理,是“先采集后处理”所以是非时实的。怎样实现时实处理?
上一段解释了什么是实时处理,下面来介绍怎样用处理器(比如单片机、DSP、ARM啥的)进行实时处理,通过上一段我们知道需要一个能够保证处理单元在特定的时刻进行处理的信号,这个信号可以有很多种形式,一般常用的就是利用处理器里面的定时器计数一段规定好的时间后然后产生一个溢出中断,并把处理单元的代码写到这个定时器中断程序中。这样定时器每隔一段时间就会就会进入一次中断并执行处理单元的程序,这样就实现了实时处理。基于C的LMS算法
关于LMS相关的理论和Matlab仿真可以查看博客文章(浅谈自适应滤波器)这里不再赘述,下面将给出LMS算法的C语言代码LMS.c文件
/*******************************************************************************************************************************************************************
* 文件名:LMS.c
* 作者: IRONMAN
* 日期: 2016.09.04
* 版本: V1.0
* 说明: 此源文件基于c66x内核实现了最小均方算法(LMS)
*
* 算法递推形式:
* 估计瞬时误差: e(k) = d(k) - x'(k)w(k) (1)
* 估计滤波系数矢量:w(k+1) = w(k) + 2 niu e(k)x(k) (2)
* 初始条件: w(0) = 0;
*
* *****************************************************************************************************************************************************************/
#include
{
w_forward_ptr[i] = w_ptr[i] + temp*x_ptr[i];
w_forward_ptr[i+1] = w_ptr[i+1] + temp*x_ptr[i+1];
w_forward_ptr[i+2] = w_ptr[i+2] + temp*x_ptr[i+2];
w_forward_ptr[i+3] = w_ptr[i+3] + temp*x_ptr[i+3];
w_forward_ptr[i+4] = w_ptr[i+4] + temp*x_ptr[i+4];
w_forward_ptr[i+5] = w_ptr[i+5] + temp*x_ptr[i+5];
w_forward_ptr[i+6] = w_ptr[i+6] + temp*x_ptr[i+6];
w_forward_ptr[i+7] = w_ptr[i+7] + temp*x_ptr[i+7];
}
/**************************************************************************************************************************************/
/************************************************************变量更替*******************************************************************/
/**************************************************************************************************************************************/
Temp_w_ptr = w_forward_ptr; //新旧滤波系数矢量指针交换
w_forward_ptr = w_ptr;
w_ptr = Temp_w_ptr;
} - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
#ifndef LMS_H_
#define LMS_H_
#include "Adaptive_filter.h"
#define LMS_M 16 //定义FIR滤波器的阶数 为保证高速运算须为8的倍数
#define LMS_NIU 0.0001 //定义收敛因子
extern float lms_x[LMS_M];
extern Adaptive_Filter_In lms_param_in;
extern Adaptive_Filter_Out lms_param_out;
extern void LMS_Gradient_Instantaneous_Estimates(Adaptive_Filter_In *lms_in, Adaptive_Filter_Out* lms_out);
#endif- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
#ifndef ADAPTIVE_FITLER_H_
#define ADAPTIVE_FITLER_H_
//定义输入参数结构体
typedef struct
{
float *x_ptr; //指向输入数组矢量X的指针
int length_x; //矢量X的长度,也即FIR滤波器的长度
float d; //输入参考数据
}Adaptive_Filter_In;
//定义输出参数结构体
typedef struct
{
float y; //滤波器的输出
float error; //误差输出
}Adaptive_Filter_Out;
#endif /* ADAPTIVE_FITLER_H_ */
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
运行的处理器是TMS320C6678 DSP,下面将给出在上面运行的结果。
基于TMS320C6678运行结果
首先给出在主函数中调用和产生仿真信号的代码实验的类型是信号增强,信号的类型和Matlab上的一样以便做对比。程序中调用了dsplib.h中的向量点乘运算函数,如果不是在DSP上或者没有DSPlib的可以自己编写该函数,也不难。
#include signal[i] = sinsp(2*PI*F1*i*Ts) + 0.5*sinsp(2*PI*F2*i*Ts) + 0.25*sinsp(2*PI*F3*i*Ts);
noise[i] = 5*sinsp(2*PI*F4*i*Ts+PI/2);
signal_noise[i] = signal[i] + 0.2*noise[i];
if(i>0)
signal_noise[i] += 0.15*noise[i-1];
if(i>1)
signal_noise[i] += 0.1*noise[i-2];
}
}
void main(void)
{
int i, j;
System_init();
make_data();
memset((void *)lms_x, 0, sizeof(lms_x)*sizeof(float));
for(i=0;ifor(j=0;j<=i;j++)
{
lms_x[j] = noise[i-j];
}
}
else
{
for(j=0;j0];
lms_param_in.length_x = LMS_M;
LMS_Gradient_Instantaneous_Estimates(&lms_param_in, &lms_param_out); //运行瞬时梯度估计LMS算法 耗时514个时钟周期
out_error[i] = lms_param_out.error;
out_y[i] = lms_param_out.y;
}
while(1);
} - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91

该图显示的是产生的仿真信号

该图显示的是产生的噪声也即干扰

该图是将得到的噪声通过一个线性系统后和信号相加后得到的图形

该图是滤波器输出的误差(因为做的是信号的增强,所以我们感兴趣的信号是输出的误差)

该图是滤波器的输出
可以和Matlab仿真的结果进行对比,会发现它们有一些不同但差别不是很大,主要原因是运算的精度不同,在Matlab上是double float 型的,在6678上的是single float型的。