转载自：http://blog.csdn.net/tqtuuuu/article/details/6821767 无意间在CSDN上看见一哥们讨论Tecent的两道面试题，其中一道题目就是求根号2的值，并且保留指点的小数位。我想我一定是不能进Tecent了，并且我一定是一个数学小白，不，就是一个小白。查了一些资料。mark一下先...
泰勒级数     泰勒级数的冥级数如下所示：
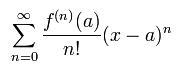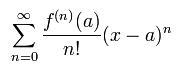    取前面两项等于0得：f(a) + f'(a)(x-a) = 0;     化简后得：x = a - f(a)/f'(a);     其中a为自变量的取值，x为a的一个近视解，使用x0代替a，x1代替x，则上式可表示为：x1 = x0 - f(x0)/f'(x0);
牛顿迭代公式     牛顿迭代法结论其实就是取泰勒级数前两项等于0求得的，为：x(n+1) = x(n) - f(x(n))/f'(x(n));
思路如下：     假设有一条曲线C，在曲线上面任选一点x0 = 1, 求的曲线的值为f(1), 即(1, f(1))为曲线上得一点。过点(1, f(1))， 作一条曲线C的切线，切线与X轴相交于点x1。同理使用x1求得x2、x3、x4......。所求得的一些列与X轴相交的点位曲线与X轴相交点得近视值。如设定某一误差e，当x(n+1)-x(n) < e,则可认为x(n+1)是曲线的一个近视解。因为x(n+1)作为曲线的解误差为可以接受的e。     其实，对于某个点，相对于曲线的切线方程是确定的，即为：f(x0) = f'(x0)(x - x0), 其中f'(x0)为切线的斜率。化简即为x1 = x0 - f(x0)/f'(x0);和泰勒级数中求得的公式不谋而合。由此可得牛顿迭代公式为：x(n+1) = x(n) - f(x(n))/f'(x(n));
最简单的C语言求根号2     采用上述方法求得了曲线的近视解，如要求根号2，可假设f(x) = x^2 - 2 = 0;即曲线x^2 -2 = 0的解即为根号2的值，通过控制误差的大小，即可求得根号2的保留小数点位数的取值。如要取得小数点为8为的根号2的值，可取误差e=0.00000001， 即误差为10的负8次方。取根号2小数点保留10位的最简单C代码如下： [cpp] view plaincopyprint? #include int main() { int i = 0; float x1 = 1, x2 = 0; float diff = 0; //diff为两次近视值之间的差，如果此差小于某一个误差值，即结束迭代 do { x2 = x1 - (x1*x1-2)/(2*x1); //如迭代公式所示，求x1的一个近视值x2 if (x2 > x1) //abs不适合求float数的绝对值，所以采用sb的判断语句 diff = x2 - x1; else diff = x1 - x2; //可以看到，误差的计算方式就是两次迭代值之间的正差 if (diff < 0.0000000001) //小数点后位数控制误差大小 break; printf("%.10f, %.10f ", x1, x2); x1 = x2; //改变x1的值为前一次跌打x2的值，继续迭代 } while (1); return 0; }
运行结果如下： [html] view plaincopyprint? # ./a.out 1.0000000000, 1.5000000000 1.5000000000, 1.4166666269 1.4166666269, 1.4142156839 1.4142156839, 1.4142135382
btw，根号2的值也就是方程x^2 - 2 = 0的解。而以上输出中第2列均为方程的解，只是精度不同而已。而精度的控制就靠diff和0.0000000001控制了。当然，代码写得很sb，并且条件全都写死在代码里面，旨在用最简单的代码讲清楚怎样使用牛顿迭代法求根号的值。     另外，大家别喷我，上述代码肯定不是最简单的，只是想要表达比较简洁，希望能够更清楚的看出牛顿迭代法的使用。