之前搞了一些数字信号处理算法编程(OC),一直没来得及整理,现在整理一下。陆续会更新,包括FFT、巴特沃斯滤波器(高低带通、高低带阻)、数据差值(线性、sinc、三次样条*)、数据压缩(等距、平均、峰值检测)和模仿matlab的STFT功能(spectrogram函数三维绘图)。
注:我比较喜欢使用matlab(也喜欢自己修改matlab的源码做测试,所以重装了好几次了,囧。。。),有部分参考matlab的算法进行(或者直接翻译为OC),算法的运行结果经常会跟matlab运算结果进行比较,算法只做学习用,转载请注明。 另外可能会有不足或者理解偏差的地方,路过的高人请不吝赐教。
好啦,进入正题。 --------------------------------------------------------------------------------------- 由于三次样条在数字信号处理中用的不是很多(或者说我用的不是很多),所以虽然实现了,这里就不贴出来了。本文讲插值运算(线性和sinc插值)的具体实现。 一、线性插值 1.原理与实现 线性插值就是在两点间插入指定个数的数据点,使得这两点间的数(包括原来的点与插入的点)满足线性关系。如下图所示黑 {MOD}的点为原来的点,红 {MOD}的点为新插入的点。原理为对相邻两点横纵坐标分别求N+1平均(N为需要插入的点数)。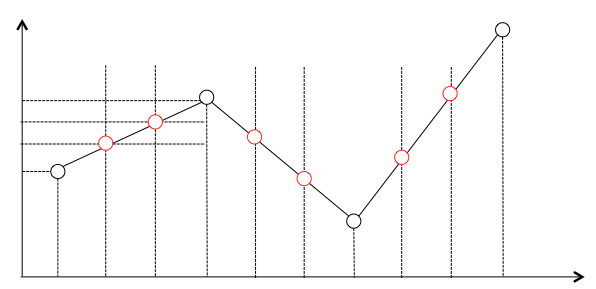
注意,为了提高效率,求平均后尽量用加法运算代替乘除法运算。 由于简单,就直接贴代码吧。。。
2.结果测试 给定数组t1,其纵坐标为1和-1交替。 t1[20] = {0.000000,0.942478,3.141593,4.084070,6.283185,7.225663,9.424778,10.367256,12.566370,13.508848,15.707963,16.650441,18.849556,19.792033,21.991148,22.933626,25.132741,26.075219,28.274333,29.216811}; 将插值后的数据点导入matlab绘制结果如下: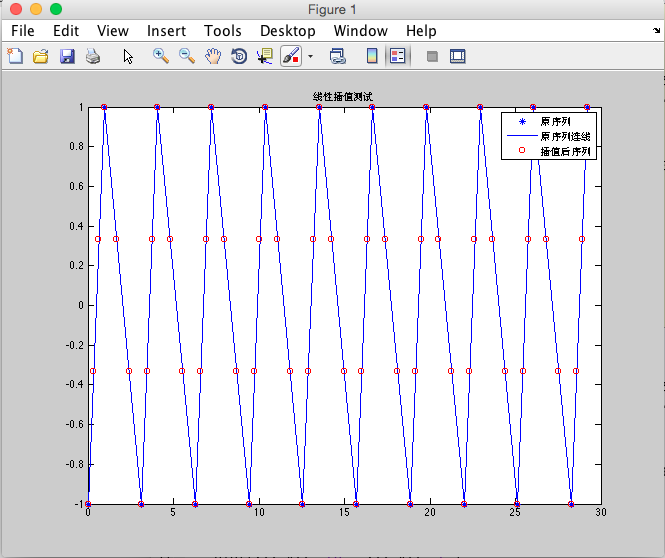
二、sinc插值
1.原理及实现 在数字信号处理应用中最常见的插值方式就是sinc插值,插值特点是使得插值后的数据更平滑、更接近于正弦波。 sinc(x)的表达式为![]()
sinc插值运算的图解如下所示:(黑 {MOD}的点为原来的点,红 {MOD}的点为新插入的点,j表示当前插值点序号。)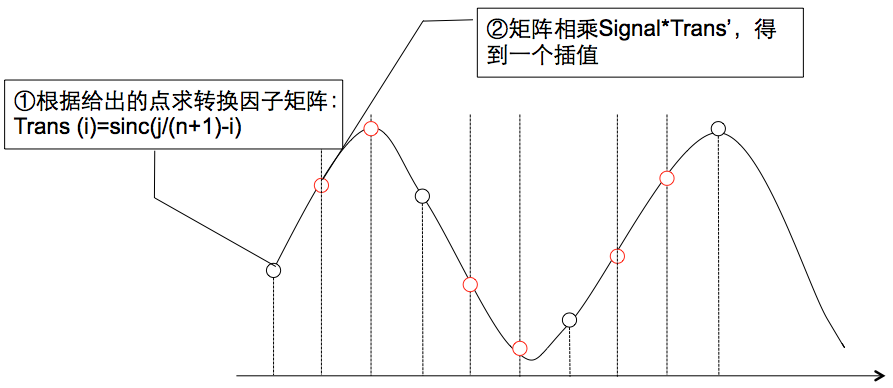
由于算法在图中已经很清楚,所以直接贴代码如下:
2.结果测试
还是将线性插值测试中用到的数组进行sinc插值(插9个值),并将插值后的数组导入matlab绘制结果如下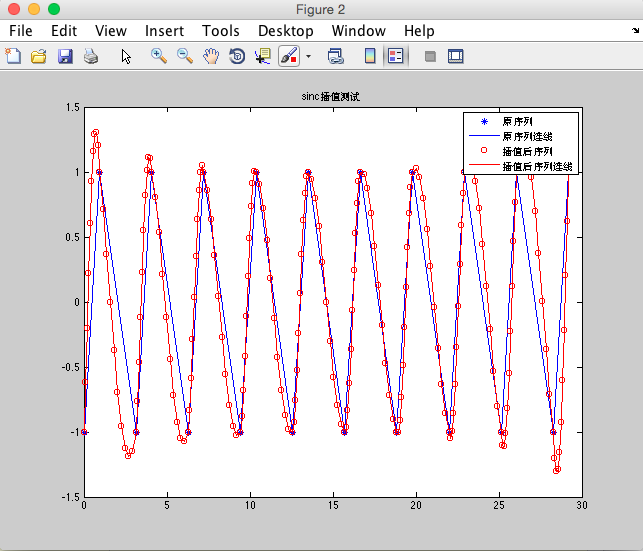
另外,将插值后的数组以matlab绘图代码的形式贴上:
=============================================== OK,插值随笔。
注:我比较喜欢使用matlab(也喜欢自己修改matlab的源码做测试,所以重装了好几次了,囧。。。),有部分参考matlab的算法进行(或者直接翻译为OC),算法的运行结果经常会跟matlab运算结果进行比较,算法只做学习用,转载请注明。 另外可能会有不足或者理解偏差的地方,路过的高人请不吝赐教。
好啦,进入正题。 --------------------------------------------------------------------------------------- 由于三次样条在数字信号处理中用的不是很多(或者说我用的不是很多),所以虽然实现了,这里就不贴出来了。本文讲插值运算(线性和sinc插值)的具体实现。 一、线性插值 1.原理与实现 线性插值就是在两点间插入指定个数的数据点,使得这两点间的数(包括原来的点与插入的点)满足线性关系。如下图所示黑 {MOD}的点为原来的点,红 {MOD}的点为新插入的点。原理为对相邻两点横纵坐标分别求N+1平均(N为需要插入的点数)。

注意,为了提高效率,求平均后尽量用加法运算代替乘除法运算。 由于简单,就直接贴代码吧。。。
/*=======================================================================
* 方法名: linearInterp
* 方法功能:线性插值方法
* 变量名称:
* xVector - 自变量,一维数组
* yVector - 因变量,一维数组
* length - 自变量数组的长度
* multiple - 采样放大倍数,插值倍数
* xInterpolated - 返回插值后的自变量值(数组)
* yInterpolated - 返回插值后的因变量值(数组)
*
* 返回值: 插值是否成功,true-成功,false-失败
*======================================================================*/
+ (Boolean)linearInterp: (float *)xVector andY: (float *)yVector andLength: (int)length andMultiple: (int) multiple andReturnX: (float *)xInterpolated andReturnY:(float*) yInterpolated
{
Boolean isInterpolatedOK = false; //插值是否成功标志
int count = multiple - 1;
int sizeOfX = length; //确定插值后数组的大小
for(int i = 0; i < sizeOfX - 1; i++)
{
xInterpolated[i * (count + 1)] = xVector[i];
yInterpolated[i * (count + 1)] = yVector[i]; //赋值原来信号的值
float deltaX = xVector[i + 1] - xVector[i];
float deltaY = yVector[i + 1] - yVector[i]; //自变量前后两个值之差
if(deltaX > 0)
{
float deltaPerX = deltaX/(count + 1); //计算因变量相邻插值距离
if(deltaY == 0) //判断前后两个数字是否相等,如果相等,中间的插值赋值为yVector[i]
{
for(int j = 1; j <= count; j++)
{
xInterpolated[i * (count + 1) + j] = xInterpolated[i * (count + 1) + j - 1] +deltaPerX; //自变量插值,自变量是自增变量,任何时候赋值的表达式一致
yInterpolated[i * (count + 1) + j] = yVector[i];
}
}
else //判断delta是否大于0,如果是,说明自变量递增
{
float deltaPerY = deltaY/(count + 1); //计算因变量相邻插值距离
for(int j = 1; j <= count; j++)
{
xInterpolated[i * (count + 1) + j] = xInterpolated[i * (count + 1) + j - 1] + deltaPerX; //自、因变量赋值
yInterpolated[i * (count + 1) + j] = yInterpolated[i * (count + 1) + j - 1] + deltaPerY;
}
}
}
else
{
isInterpolatedOK = false; //x不是单调递增的,错误,返回
return isInterpolatedOK;
}
}
//对最后一个元素赋值
xInterpolated[sizeOfX + (sizeOfX - 1) * count - 1] = xVector[sizeOfX - 1];
yInterpolated[sizeOfX + (sizeOfX - 1) * count - 1] = yVector[sizeOfX - 1];
isInterpolatedOK = true;
return isInterpolatedOK;
}2.结果测试 给定数组t1,其纵坐标为1和-1交替。 t1[20] = {0.000000,0.942478,3.141593,4.084070,6.283185,7.225663,9.424778,10.367256,12.566370,13.508848,15.707963,16.650441,18.849556,19.792033,21.991148,22.933626,25.132741,26.075219,28.274333,29.216811}; 将插值后的数据点导入matlab绘制结果如下:

二、sinc插值
1.原理及实现 在数字信号处理应用中最常见的插值方式就是sinc插值,插值特点是使得插值后的数据更平滑、更接近于正弦波。 sinc(x)的表达式为
sinc插值运算的图解如下所示:(黑 {MOD}的点为原来的点,红 {MOD}的点为新插入的点,j表示当前插值点序号。)

由于算法在图中已经很清楚,所以直接贴代码如下:
/*=======================================================================
* 方法名: SincInterp
* 方法功能:sinc插值方法
* 变量名称:
* xVector - 自变量,一维数组
* yVector - 因变量,一维数组
* length - 自变量数组的长度
* multiple - 采样放大倍数,插值倍数
* xInterpolated - 返回插值后的自变量值(数组)
* yInterpolated - 返回插值后的因变量值(数组)
*
* 返回值: 插值是否成功,true-成功,false-失败
*======================================================================*/
+ (Boolean)SincInterp:(float *)xVector andY: (float *)yVector andLength: (int)length andMultiple: (int) multiple andReturnX: (float *)xInterpolated andReturnY:(float*) yInterpolated
{
Boolean isInterpolatedOK = false; //插值成功的标志
//计算需要插入后的横坐标
isInterpolatedOK = [self xInterpolatedValue:xVector andLength:length andMultiple:multiple andXInterpolated:xInterpolated];
if(!isInterpolatedOK)
return isInterpolatedOK;
//确定插值后的长度
int toLength = [self lengthAfterInterpolated:length andMultiple:multiple];
//插值后因变量的初始化为全0
for(int i = 0; i < toLength; i++)
{
yInterpolated[i] = 0.0;
}
//计算插值后的y数组
float sincVector[length]; //用于存放sinc方法计算的值
for(int j = 0; j < toLength; j++)
{
for(int i = 0; i < length; i++)
{
sincVector[i] = [MyMath sinc:((float)j/multiple - i)]; //计算sinc用到的因子sincVector = sinc(j/4 - i)
}
for(int i = 0; i < length; i++)
{
yInterpolated[j] += yVector[i] * sincVector[i]; //矩阵相乘,yVector*sincVector',得到的时一个数
}
}
//插值成功,返回
isInterpolatedOK = true;
return isInterpolatedOK;
}2.结果测试
还是将线性插值测试中用到的数组进行sinc插值(插9个值),并将插值后的数组导入matlab绘制结果如下

另外,将插值后的数组以matlab绘图代码的形式贴上:
%% 线性插值测试
close all;
clear,clc;
% 插值前的序列
x11 = [0.000000,0.942478,3.141593,4.084070,6.283185,7.225663,9.424778,10.367256,12.566370,13.508848,15.707963,16.650441,18.849556,19.792033,21.991148,22.933626,25.132741,26.075219,28.274333,29.216811];
y11 = [-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000];
% 插值后的序列
x12 = [0.000000 0.314159 0.628319 0.942478 1.675516 2.408555 3.141593 3.455752 3.769911 4.084070 4.817108 5.550147 6.283185 6.597344 6.911504 7.225663 7.958701 8.691740 9.424778 9.738937 10.053097 10.367256 11.100294 11.833332 12.566370 12.880529 13.194689 13.508848 14.241886 14.974925 15.707963 16.022122 16.336282 16.650441 17.383479 18.116518 18.849556 19.163715 19.477874 19.792033 20.525071 21.258110 21.991148 22.305307 22.619467 22.933626 23.666664 24.399703 25.132741 25.446900 25.761060 26.075219 26.808257 27.541295 28.274333 28.588492 28.902652 29.216811];
y12 = [-1.000000 -0.333333 0.333333 1.000000 0.333333 -0.333333 -1.000000 -0.333333 0.333333 1.000000 0.333333 -0.333333 -1.000000 -0.333333 0.333333 1.000000 0.333333 -0.333333 -1.000000 -0.333333 0.333333 1.000000 0.333333 -0.333333 -1.000000 -0.333333 0.333333 1.000000 0.333333 -0.333333 -1.000000 -0.333333 0.333333 1.000000 0.333333 -0.333333 -1.000000 -0.333333 0.333333 1.000000 0.333333 -0.333333 -1.000000 -0.333333 0.333333 1.000000 0.333333 -0.333333 -1.000000 -0.333333 0.333333 1.000000 0.333333 -0.333333 -1.000000 -0.333333 0.333333 1.000000];
figure;
plot(x11,y11,'b*',x11,y11,'b');
hold on
plot(x12,y12,'ro');
hold off
title('线性插值测试');
legend('原序列','原序列连线','插值后序列');
%% sinc插值测试
%插值前序列
x21 = [0.000000,0.942478,3.141593,4.084070,6.283185,7.225663,9.424778,10.367256,12.566370,13.508848,15.707963,16.650441,18.849556,19.792033,21.991148,22.933626,25.132741,26.075219,28.274333,29.216811];
y21 = [-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000,-1.000000,1.000000];
%插值后序列
x22 = [0.000000 0.094248 0.188496 0.282743 0.376991 0.471239 0.565487 0.659735 0.753982 0.848230 0.942478 1.162389 1.382301 1.602213 1.822124 2.042035 2.261947 2.481858 2.701770 2.921681 3.141593 3.235841 3.330088 3.424336 3.518584 3.612831 3.707079 3.801327 3.895575 3.989822 4.084070 4.303981 4.523893 4.743805 4.963716 5.183628 5.403539 5.623451 5.843362 6.063274 6.283185 6.377433 6.471681 6.565928 6.660176 6.754424 6.848672 6.942920 7.037167 7.131415 7.225663 7.445575 7.665486 7.885398 8.105309 8.325221 8.545132 8.765044 8.984955 9.204867 9.424778 9.519026 9.613274 9.707521 9.801769 9.896017 9.990265 10.084513 10.178760 10.273008 10.367256 10.587167 10.807079 11.026990 11.246902 11.466813 11.686724 11.906636 12.126547 12.346459 12.566370 12.660618 12.754866 12.849113 12.943361 13.037609 13.131857 13.226105 13.320352 13.414600 13.508848 13.728760 13.948671 14.168583 14.388494 14.608406 14.828317 15.048229 15.268140 15.488052 15.707963 15.802211 15.896459 15.990706 16.084954 16.179202 16.273450 16.367698 16.461945 16.556193 16.650441 16.870352 17.090264 17.310175 17.530087 17.749998 17.969910 18.189821 18.409733 18.629644 18.849556 18.943804 19.038051 19.132299 19.226547 19.320795 19.415042 19.509290 19.603538 19.697785 19.792033 20.011944 20.231856 20.451767 20.671679 20.891590 21.111502 21.331413 21.551325 21.771236 21.991148 22.085396 22.179644 22.273891 22.368139 22.462387 22.556635 22.650883 22.745130 22.839378 22.933626 23.153537 23.373449 23.593360 23.813272 24.033183 24.253095 24.473006 24.692918 24.912829 25.132741 25.226989 25.321237 25.415484 25.509732 25.603980 25.698228 25.792476 25.886723 25.980971 26.075219 26.295130 26.515042 26.734953 26.954865 27.174776 27.394687 27.614599 27.834510 28.054422 28.274333 28.368581 28.462829 28.557076 28.651324 28.745572 28.839820 28.934068 29.028315 29.122563 29.216811];
y22 = [-1.000000 -0.617690 -0.201088 0.216756 0.602562 0.925666 1.160668 1.289632 1.303638 1.203564 1.000000 0.712316 0.366955 -0.004895 -0.370050 -0.696253 -0.955009 -1.124079 -1.189415 -1.146360 -1.000000 -0.764650 -0.462511 -0.121619 0.226711 0.550740 0.821176 1.013816 1.111717 1.106689 1.000000 0.802201 0.532115 0.215075 -0.119436 -0.440503 -0.718625 -0.928418 -1.050931 -1.075358 -1.000000 -0.832378 -0.588504 -0.291365 0.031228 0.349231 0.633156 0.856796 0.999643 1.048770 1.000000 0.858267 0.637126 0.357472 0.045568 -0.269404 -0.558074 -0.793609 -0.954209 -1.025122 -1.000000 -0.881468 -0.680861 -0.417145 -0.115130 0.196855 0.489614 0.735811 0.912521 1.003358 1.000000 0.902947 0.721464 0.472698 0.180065 -0.128949 -0.425367 -0.681431 -0.873198 -0.982778 -1.000000 -0.923357 -0.760136 -0.525734 -0.242202 0.063822 0.363610 0.629042 0.835232 0.962864 1.000000 0.943190 0.797797 0.577492 0.302967 0.000000 -0.302967 -0.577492 -0.797797 -0.943190 -1.000000 -0.962864 -0.835232 -0.629042 -0.363610 -0.063822 0.242202 0.525734 0.760136 0.923357 1.000000 0.982778 0.873198 0.681431 0.425367 0.128949 -0.180065 -0.472698 -0.721464 -0.902947 -1.000000 -1.003358 -0.912521 -0.735811 -0.489614 -0.196855 0.115130 0.417145 0.680861 0.881468 1.000000 1.025122 0.954209 0.793609 0.558074 0.269404 -0.045568 -0.357472 -0.637126 -0.858267 -1.000000 -1.048770 -0.999643 -0.856796 -0.633156 -0.349231 -0.031228 0.291365 0.588504 0.832378 1.000000 1.075358 1.050931 0.928418 0.718625 0.440503 0.119436 -0.215075 -0.532115 -0.802201 -1.000000 -1.106689 -1.111717 -1.013816 -0.821176 -0.550740 -0.226711 0.121619 0.462511 0.764650 1.000000 1.146360 1.189415 1.124079 0.955009 0.696253 0.370050 0.004895 -0.366955 -0.712316 -1.000000 -1.203564 -1.303638 -1.289632 -1.160668 -0.925666 -0.602562 -0.216756 0.201088 0.617690 1.000000];
figure;
plot(x21,y21,'b*',x21,y21,'b');
hold on
plot(x22,y22,'ro', x22,y22,'r');
hold off
title('sinc插值测试');
legend('原序列','原序列连线','插值后序列','插值后序列连线');
=============================================== OK,插值随笔。