一、实验目的
(1)加深对离散线性移不变(LSI)系统基本理论的理解,明确差分方程与系统函数之间的关系。
(2)初步了解用MATLAB语言进行离散时间系统研究的基本方法。 (3)掌握求解离散时间系统冲激响应和阶跃响应程序的编写方法,了解常用子函数。 二、实验涉及的MATLAB子函数 1.impz 功能:求解数字系统的冲激响应。 调用格式: [h,t]=impz(b,a);求解数字系统的冲激响应h,取样点数为缺省值。 [h,t]=impz(b,a,n);求解数字系统的冲激响应h,取样点数由n确定。 impz(b,a);在当前窗口用stem(t,h)函数出图。 2.dstep 功能:求解数字系统的阶跃响应。 调用格式: [h,t]=dstep(b,a);求解数字系统的阶跃响应h,取样点数为缺省值。 [h,t]=dstep(b,a,n);求解数字系统的阶跃响应h,取样点数由n确定。 dstep(b,a);在当前窗口用stairs(t,h)函数出图。 3.filter 功能:对数字系统的输入信号进行滤波处理。 调用格式: y=filter(b,a,x);对于由矢量a、b定义的数字系统,当输入信号为x时,对x中的数据进行滤波,结果放于y中,长度取max(na,nb)。 [y,zf]=filter(b,a,x);除得到结果矢量y外,还得到x的最终状态矢量zf。 y=filter(b,a,x,zi);可在zi中指定x的初始状态 4.filtic 功能:为filter函数选择初始条件。 调用格式: z=filtic(b,a,y,x);求给定输入x和y时的初始状态。 z=filtic(b,a,y);求x=0,给定输入y时的初始状态 其中,矢量x和y分别表示过去的输入和输出: x=[x(-1),x(-2),…,x(-N) y=[y(-1),y(-2),…,y(-N)] 关于该函数可参考 matlab filtic 函数应用 filter 解差分方程 dft 函数的使用。 说明:以上子函数中的b和a,分别表示系统函数H(z)中由对应的分子项和分母项系数所构成的数组。 如下面式(5-2)所示,H(z)按z-1(或z)的降幂排列。在列写b和a系数向量时,两个系数的长度必须相等,它们的同次幂系数排在同样的位置上,缺项的系数赋值为0。 在MATLAB信号处理工具箱中,许多用于多项式处理的函数,都采用以上的方法来处理分子项和分母项系数所构成的数组。在后面的实验中不再说明。 三、实验原理 1.离散LSI系统的响应与激励 由离散时间系统的时域和频域分析方法可知,一个线性移不变离散系统可以用线性常系数差分方程表示: 也可以用系统函数来表示:
也可以用系统函数来表示:
 系统函数H(z)反映了系统响应与激励间的关系。一旦上式中的bm和ak的数据确定了,则系统的性质也就确定了。其中特别注意:a0必须进行归一化处理,即a0=1。
对于复杂信号激励下的线性系统,可以将激励信号在时域中分解为单位脉冲序列或单位阶跃序列,把这些单元激励信号分别加于系统求其响应,然后把这些响应叠加,即可得到复杂信号加于系统的零状态响应。
因此,求解系统的冲激响应和阶跃响应尤为重要。由下图可以看出一个离散LSI系统响应与激励的关系。
系统函数H(z)反映了系统响应与激励间的关系。一旦上式中的bm和ak的数据确定了,则系统的性质也就确定了。其中特别注意:a0必须进行归一化处理,即a0=1。
对于复杂信号激励下的线性系统,可以将激励信号在时域中分解为单位脉冲序列或单位阶跃序列,把这些单元激励信号分别加于系统求其响应,然后把这些响应叠加,即可得到复杂信号加于系统的零状态响应。
因此,求解系统的冲激响应和阶跃响应尤为重要。由下图可以看出一个离散LSI系统响应与激励的关系。
 2.用impz和dstep子函数求解离散系统的单位冲激响应和阶跃响应
在MATLAB语言中,求解系统单位冲激响应和阶跃响应的最简单的方法是使用MATLAB提供的impz和dstep子函数。
下面举例说明使用impz和dstep子函数求解系统单位冲激响应和阶跃响应的方法。
例5-1 已知一个因果系统的差分方程为
6y(n)+2y(n-2)=x(n)+3x(n-1)+3x(n-2)+x(n-3)
满足初始条件y(-1)=0,x(-1)=0,求系统的单位冲激响应和阶跃响应。
解:首先,将y(n)项的系数a0进行归一化,得到:
y(n)+1/3* y(n-2)=1/6* x(n)+1/2* x(n-1)+1/2* x(n-2)+1/6* x(n-3)
则:
2.用impz和dstep子函数求解离散系统的单位冲激响应和阶跃响应
在MATLAB语言中,求解系统单位冲激响应和阶跃响应的最简单的方法是使用MATLAB提供的impz和dstep子函数。
下面举例说明使用impz和dstep子函数求解系统单位冲激响应和阶跃响应的方法。
例5-1 已知一个因果系统的差分方程为
6y(n)+2y(n-2)=x(n)+3x(n-1)+3x(n-2)+x(n-3)
满足初始条件y(-1)=0,x(-1)=0,求系统的单位冲激响应和阶跃响应。
解:首先,将y(n)项的系数a0进行归一化,得到:
y(n)+1/3* y(n-2)=1/6* x(n)+1/2* x(n-1)+1/2* x(n-2)+1/6* x(n-3)
则:
 编写MATLAB程序如下(取N=32点作图):
编写MATLAB程序如下(取N=32点作图):
 需要注意的是:求时域单位阶跃函数时,需要使用的是gn=dstep(b,a,n+1),而不是gn=dstep(b,a,n),在这里前者产生32* 1的矩阵(和n一样),后者产生31* 1矩阵。
但是,如果我就是想用gn=dstep(b,a,n)呢?也可以,只要把stem(n,gn);改成stem(n(1:length(gn)),gn);就可以了,代码如下:
需要注意的是:求时域单位阶跃函数时,需要使用的是gn=dstep(b,a,n+1),而不是gn=dstep(b,a,n),在这里前者产生32* 1的矩阵(和n一样),后者产生31* 1矩阵。
但是,如果我就是想用gn=dstep(b,a,n)呢?也可以,只要把stem(n,gn);改成stem(n(1:length(gn)),gn);就可以了,代码如下:
 注意,如果把stem(n,gn);改成stem(gn)的话,输出的阶跃函数会向右偏移:
注意,如果把stem(n,gn);改成stem(gn)的话,输出的阶跃函数会向右偏移:

实际上,上面的做法都不是很标准,很容易混淆。impz和dstep这两个函数的第三个参数是用来指定采样点的,而上面的代码中传入的是一个数组,这也是说我们自己指定了采样点的范围了。但是在这里还是选择指定采样点N比较好理解,而且不容易出错。 另外注意到,axis这个函数不能随便用的,对于
 例 5-2 已知一个系统函数公式
例 5-2 已知一个系统函数公式 ,求该系统的单位冲激响应和阶跃响应。
解:分析上式可知,这是一个6阶系统,直接用MATLAB语言列出其bm和ak系数:
,求该系统的单位冲激响应和阶跃响应。
解:分析上式可知,这是一个6阶系统,直接用MATLAB语言列出其bm和ak系数:
a=[1,0,0.34319,0,0.60439,0,0.20407];
b=[0.1321,0,-0.3963,0,0.3963,0,-0.1321]; 代码:
 3.用filtic和filter子函数求解离散系统的单位冲激响应
MATLAB提供了两个子函数filtic和filter来求解离散系统的响应。
当输入信号为单位冲激信号时,求得的响应即为系统的单位冲激响应;
当输入信号为单位阶跃信号时,求得的响应即为系统的单位阶跃响应。
例5-3 已知一个因果系统的差分方程为 6y(n)-2y(n-4)=x(n)-3x(n-2)+3x(n-4)-x(n-6),满足初始条件y(-1)=0,x(-1)=0,求系统的单位冲激响应和单位阶跃响应。时间轴上N取32点作图。
解:将y(n)项的系数a0进行归一化,得到: y(n)-1/3* y(n-4)=1/6* x(n)-1/2* x(n-2)+1/6* x(n-4)-1/6* x(n-6)
代码为:
3.用filtic和filter子函数求解离散系统的单位冲激响应
MATLAB提供了两个子函数filtic和filter来求解离散系统的响应。
当输入信号为单位冲激信号时,求得的响应即为系统的单位冲激响应;
当输入信号为单位阶跃信号时,求得的响应即为系统的单位阶跃响应。
例5-3 已知一个因果系统的差分方程为 6y(n)-2y(n-4)=x(n)-3x(n-2)+3x(n-4)-x(n-6),满足初始条件y(-1)=0,x(-1)=0,求系统的单位冲激响应和单位阶跃响应。时间轴上N取32点作图。
解:将y(n)项的系数a0进行归一化,得到: y(n)-1/3* y(n-4)=1/6* x(n)-1/2* x(n-2)+1/6* x(n-4)-1/6* x(n-6)
代码为:
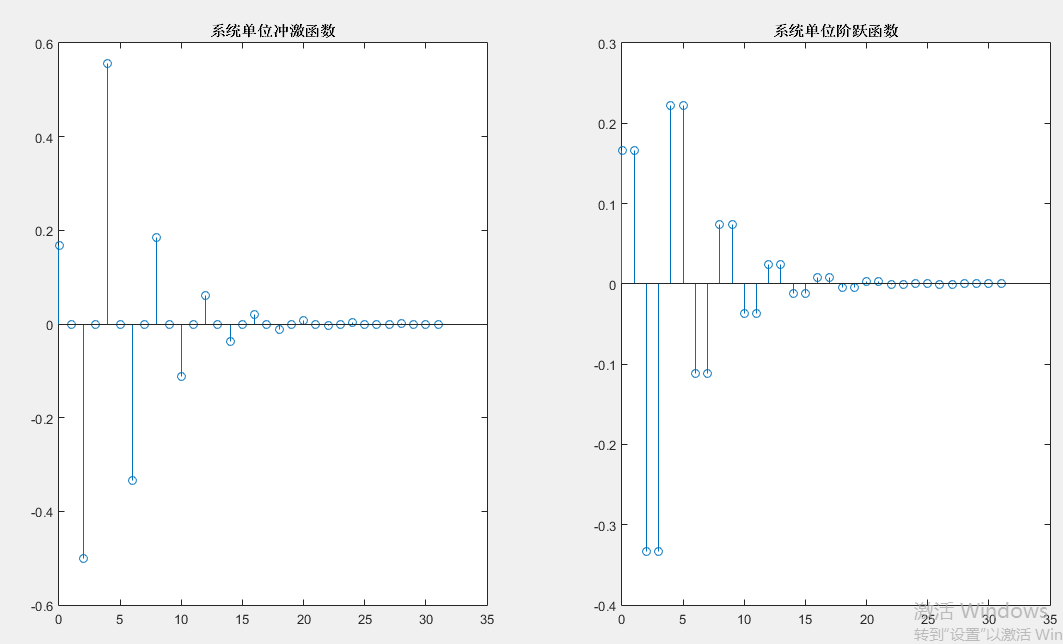 四、实验任务
(1)已知离散线性时不变系统的差分方程,请分别用impz和dstep子函数、filtic和filter子函数两种方法求解系统的冲激响应和阶跃响应。
四、实验任务
(1)已知离散线性时不变系统的差分方程,请分别用impz和dstep子函数、filtic和filter子函数两种方法求解系统的冲激响应和阶跃响应。
①x(n)+x(n-6)=y(n)
②2y(n)-3y(n-1)+y(n-2)=x(n-1) 解:下面均以时间轴上N取32点作图。
①:使用impz和dstep子函数:
代码:
 使用filtic和filter子函数:
使用filtic和filter子函数:
代码:

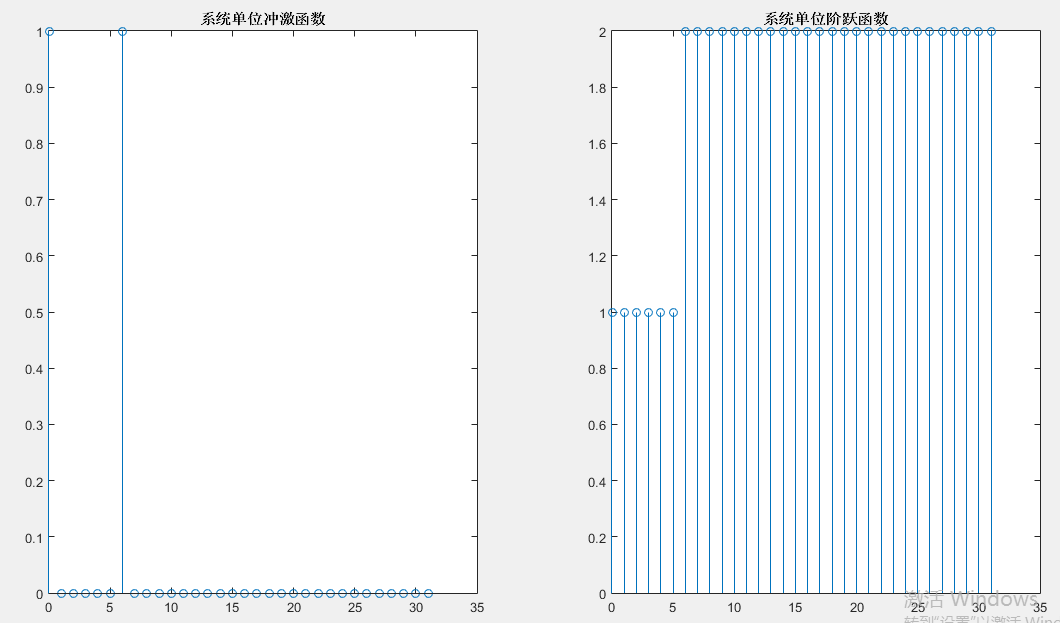
②:使用impz和dstep子函数:
代码:
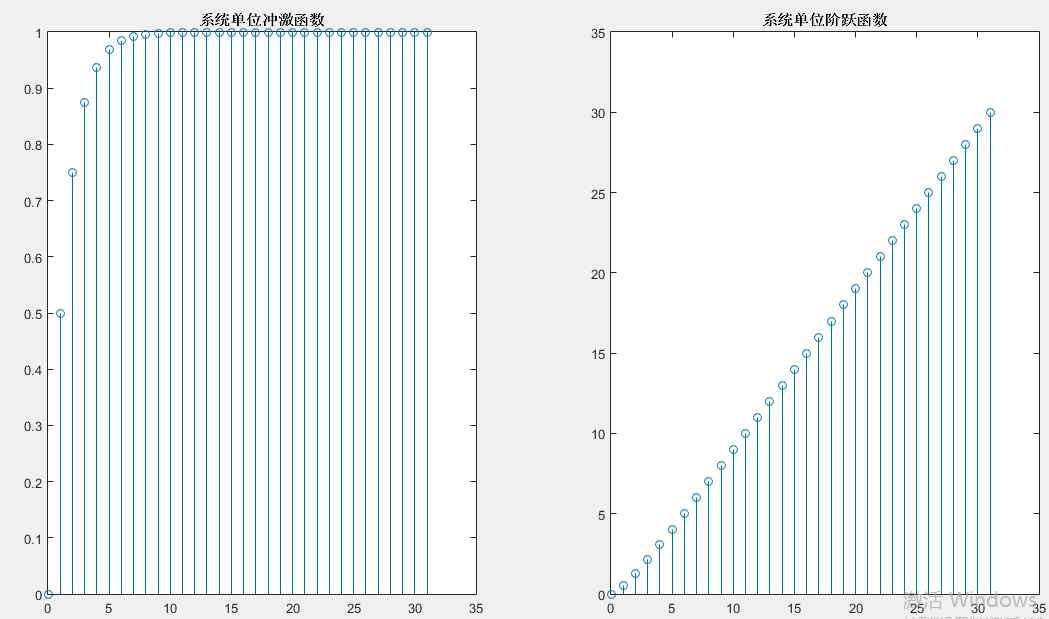 使用filtic和filter子函数:
使用filtic和filter子函数:
代码:
 (2)已知离散线性时不变系统的系统函数,请分别用impz和dstep子函数、filtic和filter子函数两种方法求解系统的冲激响应和阶跃响应。
(2)已知离散线性时不变系统的系统函数,请分别用impz和dstep子函数、filtic和filter子函数两种方法求解系统的冲激响应和阶跃响应。
 其实给出系统函数和差分方程是没有区别的。
解:下面均以时间轴上N取32点作图。
其实给出系统函数和差分方程是没有区别的。
解:下面均以时间轴上N取32点作图。
①:使用impz和dstep子函数:
代码:

使用filtic和filter子函数:
代码:
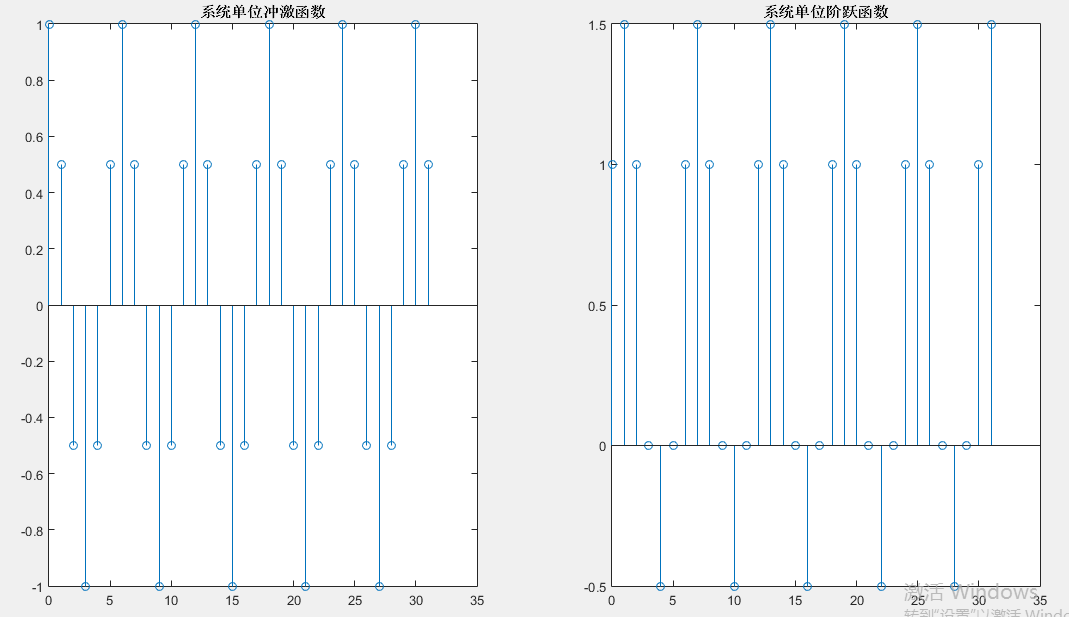 ②:使用impz和dstep子函数:
②:使用impz和dstep子函数:
代码:
 使用filtic和filter子函数:
使用filtic和filter子函数:
代码:
 思考题:
思考题:
①离散LSI系统的差分方程和系统函数有何联系?公式中的bm和ak系数在编写程序时须注意什么问题? 对差分方程两边同时进行傅里叶变换后整合化简后的结果就是系统函数。公式中的bm和ak系数在编写程序时须注意补上缺项以及搞清楚两者分别对应的是输入信号还是输出信号的系数。(bm对应x[n]、 ak对应y[n]) ②简述用子函数filter求解离散系统的单位冲激响应和单位阶跃响应的基本思路。 1.根据给定的差分方程和系统函数求出bm和ak
2.用filtic函数求出初始状态求等效初始条件的输入序列xi ,若没有初始条件则不用
3.用filter函数结合xi、bm、ak、单位冲激函数得到单位冲激响应(若没有初始条件则不用xi)
4.用filter函数结合xi、bm、ak、单位阶跃函数得到单位阶跃响应(若没有初始条件则不用xi)
(2)初步了解用MATLAB语言进行离散时间系统研究的基本方法。 (3)掌握求解离散时间系统冲激响应和阶跃响应程序的编写方法,了解常用子函数。 二、实验涉及的MATLAB子函数 1.impz 功能:求解数字系统的冲激响应。 调用格式: [h,t]=impz(b,a);求解数字系统的冲激响应h,取样点数为缺省值。 [h,t]=impz(b,a,n);求解数字系统的冲激响应h,取样点数由n确定。 impz(b,a);在当前窗口用stem(t,h)函数出图。 2.dstep 功能:求解数字系统的阶跃响应。 调用格式: [h,t]=dstep(b,a);求解数字系统的阶跃响应h,取样点数为缺省值。 [h,t]=dstep(b,a,n);求解数字系统的阶跃响应h,取样点数由n确定。 dstep(b,a);在当前窗口用stairs(t,h)函数出图。 3.filter 功能:对数字系统的输入信号进行滤波处理。 调用格式: y=filter(b,a,x);对于由矢量a、b定义的数字系统,当输入信号为x时,对x中的数据进行滤波,结果放于y中,长度取max(na,nb)。 [y,zf]=filter(b,a,x);除得到结果矢量y外,还得到x的最终状态矢量zf。 y=filter(b,a,x,zi);可在zi中指定x的初始状态 4.filtic 功能:为filter函数选择初始条件。 调用格式: z=filtic(b,a,y,x);求给定输入x和y时的初始状态。 z=filtic(b,a,y);求x=0,给定输入y时的初始状态 其中,矢量x和y分别表示过去的输入和输出: x=[x(-1),x(-2),…,x(-N) y=[y(-1),y(-2),…,y(-N)] 关于该函数可参考 matlab filtic 函数应用 filter 解差分方程 dft 函数的使用。 说明:以上子函数中的b和a,分别表示系统函数H(z)中由对应的分子项和分母项系数所构成的数组。 如下面式(5-2)所示,H(z)按z-1(或z)的降幂排列。在列写b和a系数向量时,两个系数的长度必须相等,它们的同次幂系数排在同样的位置上,缺项的系数赋值为0。 在MATLAB信号处理工具箱中,许多用于多项式处理的函数,都采用以上的方法来处理分子项和分母项系数所构成的数组。在后面的实验中不再说明。 三、实验原理 1.离散LSI系统的响应与激励 由离散时间系统的时域和频域分析方法可知,一个线性移不变离散系统可以用线性常系数差分方程表示:
 也可以用系统函数来表示:
也可以用系统函数来表示:
 系统函数H(z)反映了系统响应与激励间的关系。一旦上式中的bm和ak的数据确定了,则系统的性质也就确定了。其中特别注意:a0必须进行归一化处理,即a0=1。
对于复杂信号激励下的线性系统,可以将激励信号在时域中分解为单位脉冲序列或单位阶跃序列,把这些单元激励信号分别加于系统求其响应,然后把这些响应叠加,即可得到复杂信号加于系统的零状态响应。
因此,求解系统的冲激响应和阶跃响应尤为重要。由下图可以看出一个离散LSI系统响应与激励的关系。
系统函数H(z)反映了系统响应与激励间的关系。一旦上式中的bm和ak的数据确定了,则系统的性质也就确定了。其中特别注意:a0必须进行归一化处理,即a0=1。
对于复杂信号激励下的线性系统,可以将激励信号在时域中分解为单位脉冲序列或单位阶跃序列,把这些单元激励信号分别加于系统求其响应,然后把这些响应叠加,即可得到复杂信号加于系统的零状态响应。
因此,求解系统的冲激响应和阶跃响应尤为重要。由下图可以看出一个离散LSI系统响应与激励的关系。
 2.用impz和dstep子函数求解离散系统的单位冲激响应和阶跃响应
在MATLAB语言中,求解系统单位冲激响应和阶跃响应的最简单的方法是使用MATLAB提供的impz和dstep子函数。
下面举例说明使用impz和dstep子函数求解系统单位冲激响应和阶跃响应的方法。
例5-1 已知一个因果系统的差分方程为
6y(n)+2y(n-2)=x(n)+3x(n-1)+3x(n-2)+x(n-3)
满足初始条件y(-1)=0,x(-1)=0,求系统的单位冲激响应和阶跃响应。
解:首先,将y(n)项的系数a0进行归一化,得到:
y(n)+1/3* y(n-2)=1/6* x(n)+1/2* x(n-1)+1/2* x(n-2)+1/6* x(n-3)
则:
2.用impz和dstep子函数求解离散系统的单位冲激响应和阶跃响应
在MATLAB语言中,求解系统单位冲激响应和阶跃响应的最简单的方法是使用MATLAB提供的impz和dstep子函数。
下面举例说明使用impz和dstep子函数求解系统单位冲激响应和阶跃响应的方法。
例5-1 已知一个因果系统的差分方程为
6y(n)+2y(n-2)=x(n)+3x(n-1)+3x(n-2)+x(n-3)
满足初始条件y(-1)=0,x(-1)=0,求系统的单位冲激响应和阶跃响应。
解:首先,将y(n)项的系数a0进行归一化,得到:
y(n)+1/3* y(n-2)=1/6* x(n)+1/2* x(n-1)+1/2* x(n-2)+1/6* x(n-3)
则:  编写MATLAB程序如下(取N=32点作图):
编写MATLAB程序如下(取N=32点作图):
a=[1 0 1/3 0];
b=[1/6 1/2 1/2 1/6];
N=32;%作图点数
n=0:N-1;
hn=impz(b,a,n);%时域单位冲激函数
gn=dstep(b,a,n+1);%时域单位阶跃函数
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出结果:  需要注意的是:求时域单位阶跃函数时,需要使用的是gn=dstep(b,a,n+1),而不是gn=dstep(b,a,n),在这里前者产生32* 1的矩阵(和n一样),后者产生31* 1矩阵。
但是,如果我就是想用gn=dstep(b,a,n)呢?也可以,只要把stem(n,gn);改成stem(n(1:length(gn)),gn);就可以了,代码如下:
需要注意的是:求时域单位阶跃函数时,需要使用的是gn=dstep(b,a,n+1),而不是gn=dstep(b,a,n),在这里前者产生32* 1的矩阵(和n一样),后者产生31* 1矩阵。
但是,如果我就是想用gn=dstep(b,a,n)呢?也可以,只要把stem(n,gn);改成stem(n(1:length(gn)),gn);就可以了,代码如下:
a=[1 0 1/3 0];
b=[1/6 1/2 1/2 1/6];
N=32;%作图点数
n=0:N-1;
hn=impz(b,a,n);%时域单位冲激函数
gn=dstep(b,a,n);%时域单位阶跃函数
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n(1:length(gn)),gn);
title('系统单位阶跃函数')
axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出:  注意,如果把stem(n,gn);改成stem(gn)的话,输出的阶跃函数会向右偏移:
注意,如果把stem(n,gn);改成stem(gn)的话,输出的阶跃函数会向右偏移: 
实际上,上面的做法都不是很标准,很容易混淆。impz和dstep这两个函数的第三个参数是用来指定采样点的,而上面的代码中传入的是一个数组,这也是说我们自己指定了采样点的范围了。但是在这里还是选择指定采样点N比较好理解,而且不容易出错。 另外注意到,axis这个函数不能随便用的,对于
axis([0 N 1.1*min(hn) 1.1*max(hn)]),,如果9.5<=hn<=10,那么1.1*min(hn)就超过了hn的最大值了,这样就看不到图像了!!!
axis这个函数是人为用来调整的,要用之前最好先绘出图像,看了图像的数值范围后再使用。
下面给出代码:
a=[1 0 1/3 0];
b=[1/6 1/2 1/2 1/6];
N=32;%作图点数
n=0:N-1;
hn=impz(b,a,N);%时域单位冲激函数
gn=dstep(b,a,N);%时域单位阶跃函数
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
%axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
%axis([0 N 0 1.1*max(gn)])
输出结果:  例 5-2 已知一个系统函数公式
例 5-2 已知一个系统函数公式 ,求该系统的单位冲激响应和阶跃响应。
解:分析上式可知,这是一个6阶系统,直接用MATLAB语言列出其bm和ak系数:
,求该系统的单位冲激响应和阶跃响应。
解:分析上式可知,这是一个6阶系统,直接用MATLAB语言列出其bm和ak系数: a=[1,0,0.34319,0,0.60439,0,0.20407];
b=[0.1321,0,-0.3963,0,0.3963,0,-0.1321]; 代码:
a=[1 0 0.34319 0 0.60439 0 0.20407];
b=[0.1321 0 -0.3963 0 0.3963 0 -0.1321];
N=32;%作图点数
n=0:N-1;
hn=impz(b,a,N);%时域单位冲激函数
gn=dstep(b,a,N);%时域单位阶跃函数
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
%axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
%axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出结果:  3.用filtic和filter子函数求解离散系统的单位冲激响应
MATLAB提供了两个子函数filtic和filter来求解离散系统的响应。
当输入信号为单位冲激信号时,求得的响应即为系统的单位冲激响应;
当输入信号为单位阶跃信号时,求得的响应即为系统的单位阶跃响应。
例5-3 已知一个因果系统的差分方程为 6y(n)-2y(n-4)=x(n)-3x(n-2)+3x(n-4)-x(n-6),满足初始条件y(-1)=0,x(-1)=0,求系统的单位冲激响应和单位阶跃响应。时间轴上N取32点作图。
解:将y(n)项的系数a0进行归一化,得到: y(n)-1/3* y(n-4)=1/6* x(n)-1/2* x(n-2)+1/6* x(n-4)-1/6* x(n-6)
代码为:
3.用filtic和filter子函数求解离散系统的单位冲激响应
MATLAB提供了两个子函数filtic和filter来求解离散系统的响应。
当输入信号为单位冲激信号时,求得的响应即为系统的单位冲激响应;
当输入信号为单位阶跃信号时,求得的响应即为系统的单位阶跃响应。
例5-3 已知一个因果系统的差分方程为 6y(n)-2y(n-4)=x(n)-3x(n-2)+3x(n-4)-x(n-6),满足初始条件y(-1)=0,x(-1)=0,求系统的单位冲激响应和单位阶跃响应。时间轴上N取32点作图。
解:将y(n)项的系数a0进行归一化,得到: y(n)-1/3* y(n-4)=1/6* x(n)-1/2* x(n-2)+1/6* x(n-4)-1/6* x(n-6)
代码为:
a=[1 0 0 0 -1/3 0 0];
b=[1/6 0 -1/2 0 1/2 0 -1/6];
N=32;%作图点数
n=0:N-1;
x1= n==0;%建立输入单位冲激信号x1(n)
x0=0;y0=0;%初始条件
xi=filtic(b,a,y0,x0);%求等效初始条件的输入序列
hn=filter(b,a,x1,xi);%对输入单位冲激信号进行滤波,求单位冲激响应
x2= n>=0;%建立输入单位阶跃信号x2(n)
gn=filter(b,a,x2,xi);%对输入单位冲激信号进行滤波,求单位冲激响应
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
%axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
%axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出结果:  四、实验任务
(1)已知离散线性时不变系统的差分方程,请分别用impz和dstep子函数、filtic和filter子函数两种方法求解系统的冲激响应和阶跃响应。
四、实验任务
(1)已知离散线性时不变系统的差分方程,请分别用impz和dstep子函数、filtic和filter子函数两种方法求解系统的冲激响应和阶跃响应。 ①x(n)+x(n-6)=y(n)
②2y(n)-3y(n-1)+y(n-2)=x(n-1) 解:下面均以时间轴上N取32点作图。
①:使用impz和dstep子函数:
代码:
a=[1 0 0 0 0 0 0];
b=[1 0 0 0 0 0 1];
N=32;%作图点数
n=0:N-1;
hn=impz(b,a,N);%时域单位冲激函数
gn=dstep(b,a,N);%时域单位阶跃函数
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
%axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
%axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出结果:  使用filtic和filter子函数:
使用filtic和filter子函数: 代码:
a=[1 0 0 0 0 0 0];
b=[1 0 0 0 0 0 1];
tmp=a(1);
a=a./tmp;%归一化
b=b./tmp;
N=32;%作图点数
n=0:N-1;
x1= n==0;%建立输入单位冲激信号x1(n)
%xi=filtic(b,a,0);%求等效初始条件的输入序列
hn=filter(b,a,x1);%对输入单位冲激信号进行滤波,求单位冲激响应
x2= n>=0;%建立输入单位阶跃信号x2(n)
gn=filter(b,a,x2);%对输入单位冲激信号进行滤波,求单位冲激响应
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
%axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
%axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出结果: 
②:使用impz和dstep子函数:
代码:
a=[2 -3 1];
b=[0 1 0];
tmp=a(1);
a=a./tmp;%归一化
b=b./tmp;
N=32;%作图点数
n=0:N-1;
hn=impz(b,a,N);%时域单位冲激函数
gn=dstep(b,a,N);%时域单位阶跃函数
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
%axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
%axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出结果:  使用filtic和filter子函数:
使用filtic和filter子函数: 代码:
a=[2 -3 1];
b=[0 1 0];
tmp=a(1);
a=a./tmp;%归一化
b=b./tmp;
N=32;%作图点数
n=0:N-1;
x1= n==0;%建立输入单位冲激信号x1(n)
%xi=filtic(b,a,0);%求等效初始条件的输入序列
hn=filter(b,a,x1);%对输入单位冲激信号进行滤波,求单位冲激响应
x2= n>=0;%建立输入单位阶跃信号x2(n)
gn=filter(b,a,x2);%对输入单位冲激信号进行滤波,求单位冲激响应
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
%axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
%axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出结果:  (2)已知离散线性时不变系统的系统函数,请分别用impz和dstep子函数、filtic和filter子函数两种方法求解系统的冲激响应和阶跃响应。
(2)已知离散线性时不变系统的系统函数,请分别用impz和dstep子函数、filtic和filter子函数两种方法求解系统的冲激响应和阶跃响应。  其实给出系统函数和差分方程是没有区别的。
解:下面均以时间轴上N取32点作图。
其实给出系统函数和差分方程是没有区别的。
解:下面均以时间轴上N取32点作图。 ①:使用impz和dstep子函数:
代码:
a=[1 -1 1];
b=[1 -0.5 0];
tmp=a(1);
a=a./tmp;%归一化
b=b./tmp;
N=32;%作图点数
n=0:N-1;
hn=impz(b,a,N);%时域单位冲激函数
gn=dstep(b,a,N);%时域单位阶跃函数
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
%axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
%axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出结果: 
使用filtic和filter子函数:
代码:
a=[1 -1 1];
b=[1 -0.5 0];
tmp=a(1);
a=a./tmp;%归一化
b=b./tmp;
N=32;%作图点数
n=0:N-1;
x1= n==0;%建立输入单位冲激信号x1(n)
%xi=filtic(b,a,0);%求等效初始条件的输入序列
hn=filter(b,a,x1);%对输入单位冲激信号进行滤波,求单位冲激响应
x2= n>=0;%建立输入单位阶跃信号x2(n)
gn=filter(b,a,x2);%对输入单位冲激信号进行滤波,求单位冲激响应
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
%axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
%axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出结果:  ②:使用impz和dstep子函数:
②:使用impz和dstep子函数: 代码:
a=[1 0 0 0 0 0];
b=[1 0.5 -0.5 -1 -0.5 1];
tmp=a(1);
a=a./tmp;%归一化
b=b./tmp;
N=32;%作图点数
n=0:N-1;
hn=impz(b,a,N);%时域单位冲激函数
gn=dstep(b,a,N);%时域单位阶跃函数
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
%axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
%axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出结果:  使用filtic和filter子函数:
使用filtic和filter子函数: 代码:
a=[1 0 0 0 0 0];
b=[1 0.5 -0.5 -1 -0.5 1];
tmp=a(1);
a=a./tmp;%归一化
b=b./tmp;
N=32;%作图点数
n=0:N-1;
x1= n==0;%建立输入单位冲激信号x1(n)
%xi=filtic(b,a,0);%求等效初始条件的输入序列
hn=filter(b,a,x1);%对输入单位冲激信号进行滤波,求单位冲激响应
x2= n>=0;%建立输入单位阶跃信号x2(n)
gn=filter(b,a,x2);%对输入单位冲激信号进行滤波,求单位冲激响应
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
%axis([0 N 1.1*min(hn) 1.1*max(hn)])
subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
%axis([0 N 1.1*min(gn) 1.1*max(gn)])
输出结果:  思考题:
思考题: ①离散LSI系统的差分方程和系统函数有何联系?公式中的bm和ak系数在编写程序时须注意什么问题? 对差分方程两边同时进行傅里叶变换后整合化简后的结果就是系统函数。公式中的bm和ak系数在编写程序时须注意补上缺项以及搞清楚两者分别对应的是输入信号还是输出信号的系数。(bm对应x[n]、 ak对应y[n]) ②简述用子函数filter求解离散系统的单位冲激响应和单位阶跃响应的基本思路。 1.根据给定的差分方程和系统函数求出bm和ak
2.用filtic函数求出初始状态求等效初始条件的输入序列xi ,若没有初始条件则不用
3.用filter函数结合xi、bm、ak、单位冲激函数得到单位冲激响应(若没有初始条件则不用xi)
4.用filter函数结合xi、bm、ak、单位阶跃函数得到单位阶跃响应(若没有初始条件则不用xi)