class="markdown_views prism-kimbie-light">
(2)修改程序P1.1,产生单位步长序列u(n+1)并绘图。
(3)修改程序P1.4,产生长度为50、频率为0.08、振幅为2.5、相移为90度的一个正弦序列并绘图,该序列的周期是多少?
(2)修改程序P2.4,其中D=15, w1=0.4π,w2=1.6π并绘图,该离散时间系统是时不变吗?
(3)修改程序P2.5,产生如下因果线性时不变系统的冲激响应的前45个样本并绘图:

(4)运行程序P2.7,对序列h(n)和x(n)求卷积生成y(n),并用FIR滤波器h(n)对输入x(n)滤波,求得y1(n);y(n)和y1(n)有差别吗?为什么要使用对x(n)补零后得到的x1(n)作为输入来产生y1(n)?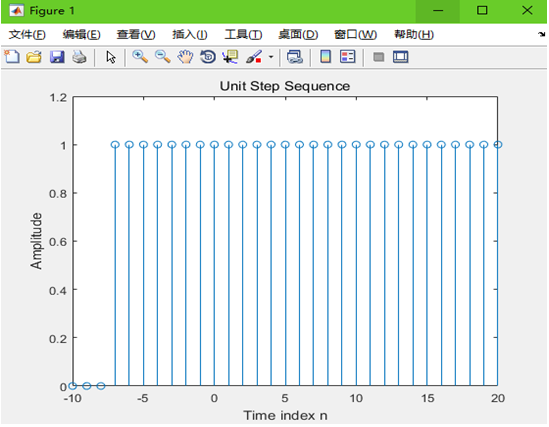
(2)实验结果: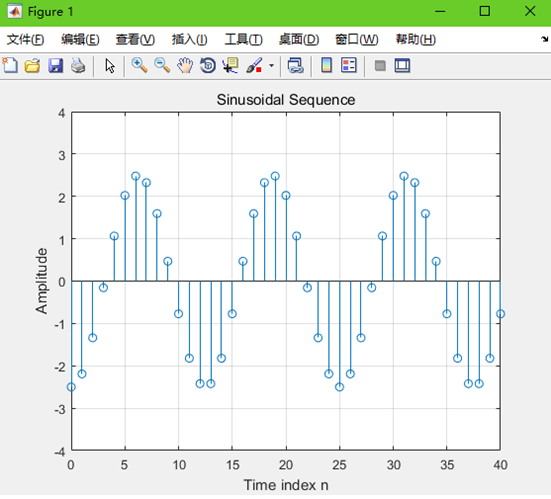
(3)实验结果: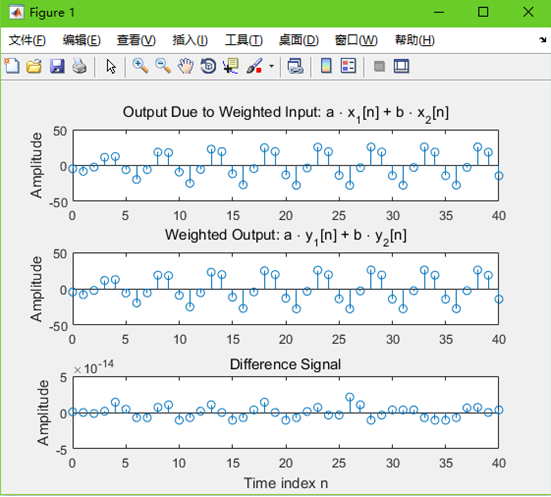

(2)实验结果:
(3)实验结果: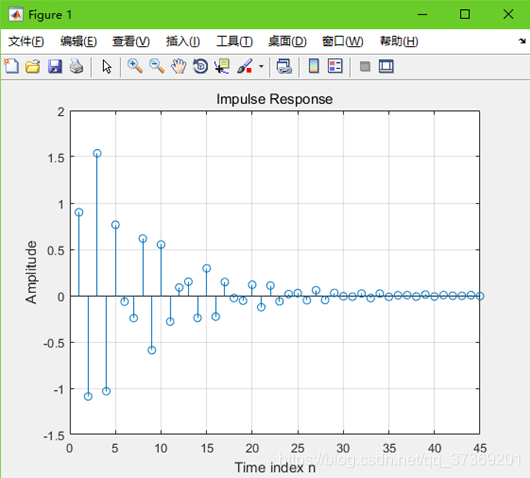
(4)实验结果 没有差别。对x[n]补零是因为filter函数产生的输出序列和输入序列相等,而两信号卷积得到的序列长度为N1+N2-1,所以要补相应个数的零。
文章目录
一、实验目的:
熟悉Mat lab中产生信号和绘制信号的基本命令,掌握产生离散时间信号的基本方法;掌握离散时间系统对输入信号的简单运算处理,验证离散时间系统有关特性。二、实验内容及要求:
1. 离散时间信号的时域分析:
(1)修改程序P1.1,产生单位抽样序列δ(n-11)并绘图。(2)修改程序P1.1,产生单位步长序列u(n+1)并绘图。
(3)修改程序P1.4,产生长度为50、频率为0.08、振幅为2.5、相移为90度的一个正弦序列并绘图,该序列的周期是多少?
2. 离散时间系统的时域分析:
(1)修改程序P2.3,其中a=4, b=-6, w1=0.4π,w2=1.6π并绘图,该离散时间系统是线性吗?(2)修改程序P2.4,其中D=15, w1=0.4π,w2=1.6π并绘图,该离散时间系统是时不变吗?
(3)修改程序P2.5,产生如下因果线性时不变系统的冲激响应的前45个样本并绘图:

(4)运行程序P2.7,对序列h(n)和x(n)求卷积生成y(n),并用FIR滤波器h(n)对输入x(n)滤波,求得y1(n);y(n)和y1(n)有差别吗?为什么要使用对x(n)补零后得到的x1(n)作为输入来产生y1(n)?
三、实验结果及问题回答:
1. 离散时间信号的时域分析:
(1)实验结果:% Program P1_1
% Generation of a Unit Sample Sequence
clf;
% Generate a vector from -10 to 20
n = -10:20;
% Generate the unit sample sequence
u = [zeros(1,21) 1 zeros(1,9)];
% Plot the unit sample sequence
stem(n,u);
xlabel('Time index n');ylabel('Amplitude');
title('Unit Sample Sequence');
axis([-10 20 0 1.2]);

(2)实验结果:
% Program P1_1
% Generation of a Unit Sample Sequence
clf;
% Generate a vector from -10 to 20
n = -10:20;
% Generate the unit sample sequence
u = [zeros(1,3) ones(1,28)];
% Plot the unit sample sequence
stem(n,u);
xlabel('Time index n');ylabel('Amplitude');
title('Unit Step Sequence');
axis([-10 20 0 1.2]);

(3)实验结果:
% Program P1_4
% Generation of a sinusoidal sequence
n = 0:50;
f = 0.08;
phase = pi/2;
A = 2.5;
arg = 2*pi*f*n - phase;
x = A*sin(arg);
clf; % Clear old graph
stem(n,x); % Plot the generated sequence
axis([0 40 -4 4]);
grid;
title('Sinusoidal Sequence');
xlabel('Time index n');
ylabel('Amplitude');
axis;

2. 离散时间系统的时域分析:
(1)实验结果:% Program P2_3
% Generate the input sequences
clf;
n = 0:40;
a = 4;b = -6;
x1 = cos(4*pi*0.1*n);
x2 = cos(4*pi*0.4*n);
x = a*x1 + b*x2;
num = [2.2403 2.4908 2.2403];
den = [1 -0.4 0.75];
ic = [0 0]; % Set zero initial conditions
y1 = filter(num,den,x1,ic); % Compute the output y1[n]
y2 = filter(num,den,x2,ic); % Compute the output y2[n]
y = filter(num,den,x,ic); % Compute the output y[n]
yt = a*y1 + b*y2;
d = y - yt; % Compute the difference output d[n]
% Plot the outputs and the difference signal
subplot(3,1,1)
stem(n,y);
ylabel('Amplitude');
title('Output Due to Weighted Input: a cdot x_{1}[n] + b cdot x_{2}[n]');
subplot(3,1,2)
stem(n,yt);
ylabel('Amplitude');
title('Weighted Output: a cdot y_{1}[n] + b cdot y_{2}[n]');
subplot(3,1,3)
stem(n,d);
xlabel('Time index n');ylabel('Amplitude');
title('Difference Signal');

(2)实验结果:
% Program P2_4
% Generate the input sequences
clf;
n = 0:40; D = 15;a = 3.0;b = -2;
x = a*cos(4*pi*0.1*n) + b*cos(4*pi*0.4*n);
xd = [zeros(1,D) x];
num = [2.2403 2.4908 2.2403];
den = [1 -0.4 0.75];
ic = [0 0]; % Set initial conditions
% Compute the output y[n]
y = filter(num,den,x,ic);
% Compute the output yd[n]
yd = filter(num,den,xd,ic);
% Compute the difference output d[n]
d = y - yd(1+D:41+D);
% Plot the outputs
subplot(3,1,1)
stem(n,y);
ylabel('Amplitude');
title('Output y[n]'); grid;
subplot(3,1,2)
stem(n,yd(1:41));
ylabel('Amplitude');
title(['Output due to Delayed Input x[n ?, num2str(D),']); grid;
subplot(3,1,3)
stem(n,d);
xlabel('Time index n'); ylabel('Amplitude');
title('Difference Signal'); grid;

(3)实验结果:
%%
clf;
N = 45;
num1 = [0.9 -0.45 0.35 0.002];
den1 = [1 0.71 -0.46 -0.62];
y1 = impz(num1,den1,N);
% Plot the impulse response
figure(1)
stem(y1);
xlabel('Time index n'); ylabel('Amplitude');
title('Impulse Response'); grid;

(4)实验结果 没有差别。对x[n]补零是因为filter函数产生的输出序列和输入序列相等,而两信号卷积得到的序列长度为N1+N2-1,所以要补相应个数的零。