比例谐振（PR）控制器的学习过程记录

DSP

比例谐振（PR）控制器的学习过程记录

2019-07-13 20:18发布生成海报

站内文章 / DSP

14529 0

目录 0、前言 1、PR控制器和PI控制器对比 1.1 传递函数表达式对比 1.2 波特图对比 2、离散化预备知识 2.1 离散化表达式 2.2 离散化方法 2.3 离散化练习题 3. 使用Matlab离散PR控制器 4、逆变器仿真模型中使用PR闭环控制器

0、前言

在一个闭环控制系统中，可分为输入参考值、闭环控制器、执行机构、输出参数，反馈系数，这几个部分。

设计一款控制器，可以让系统的输出参数跟踪输入参考值，达到了控制的目的。在直流控制系统中，常用的控制器就是比例微分积分(Proportion Integration Differentiation,PID)控制器了。然而，在交流系统中，PID控制器由于对高频信号的跟踪性能较差，并不能满足设计要求。而PR控制器，对特定频率信号的跟踪效果是良好的。本文首先对PR控制器和PI控制器进行对比。然后讨论了比例谐振（Proportion, Resonant, PR）控制器的数字化实现。笔者目前在一款DCDC电路中使用过PI控制器，同时PI控制器的资料比较好找。然而PR控制器只在软件仿真中使用过，并没有在实际项目中使用。希望我和读者们，都能从本文中获益，谢谢。

1、PR控制器和PI控制器对比

1.1 传递函数表达式对比

比例积分控制器的传递函数如下： $G_{PI}left ( s ight )=K_p + frac{K_i}{s}$ 比例谐振控制器的传递函数如下： $G_{PR-ideal}left ( s ight )=K_p + frac{K_rs}{s^{2}+omega _o^{2}}$ 本文称这个PR控制器为理想的PR控制器。以上的 $G_{PR-ideal}$ 这个控制器，在下文的波特图上可见，只对单一的频率起作用。但实际上，例如逆变器，参考波形可能在频率上有正负1Hz的变化，或者由于测量采样的不确定性，因此在运用中，会用以下的变形，替代上面的Gpr-ideal。 $G_{PR}left ( s ight )=K_p + frac{2K_romega _cs}{s^{2}+2omega _cs+omega _o^{2}}$ 本文称这个PR控制器为实际的PR控制器。

1.2 波特图对比

下图是当Kp分别取为1、10、100，Ki=10时PI控制器的波特图（蓝 {MOD}是Kp=1，绿 {MOD}是Kp=10，红 {MOD}是Kp=100）。

附上实现代码：

% this is Matlab code:
Ki=10;
Kp=1;
PIs1=tf([Kp,Ki],[1,0])
Kp=10;
PIs2=tf([Kp,Ki],[1,0])
Kp=100;
PIs3=tf([Kp,Ki],[1,0])
bode(PIs1,PIs2,PIs3)
title('Bode Diagram of PI: Kp=1,10,100. Ki=10')
grid on

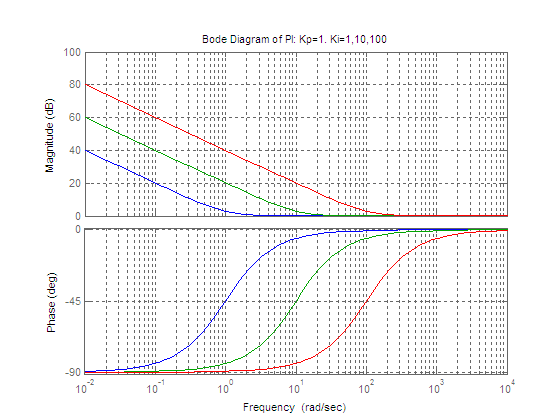
下图是当Kp=1，Ki分别取为1、10、100时PI控制器的波特图（蓝 {MOD}是Ki=1，绿 {MOD}是Ki=10，红 {MOD}是Ki=100）。

附上实现代码：

Kp=1
Ki=1
PIs1=tf([Kp,Ki],[1,0])
Ki=10
PIs2=tf([Kp,Ki],[1,0])
Ki=100
PIs3=tf([Kp,Ki],[1,0])
figure(2)
bode(PIs1,PIs2,PIs3)
grid on
title('Bode Diagram of PI: Kp=1. Ki=1,10,100')

可以看到，PI控制器对高频信号的增益会较低，而对低频信号会有较大的放大作用。假如使用PI控制器对50Hz及以上（角频率314rad/sec）的正弦波进行跟踪，系统的跟踪特性会较差。而且会把低频噪声放大。下图是当Kp分别取为1、10、100，Kr=1时理想的PR控制器的波特图（蓝 {MOD}是Kp=1，绿 {MOD}是Kp=10，红 {MOD}是Kp=100）。

附实现代码

Kr=1;
Kp=1;
PR_ideal1 = Kp + tf([Kr,0],[1,0,wo^2])
Kp=10;
PR_ideal2 = Kp + tf([Kr,0],[1,0,wo^2])
Kp=100;
PR_ideal3 = Kp + tf([Kr,0],[1,0,wo^2])
bode(PR_ideal1,PR_ideal2,PR_ideal3)
grid on
title('Bode Diagram of ideal PR: Kp = 1,10,100. Kr = 1')

下图是当Kp=1，Kr分别取为1、10、100时理想的PR控制器的波特图（蓝 {MOD}是Kr=1，绿 {MOD}是Kr=10，红 {MOD}是Kr=100）。

附实现代码

Kp=1;
Kr=1;
PR_ideal1 = Kp + tf([Kr,0],[1,0,wo^2])
Kr=10;
PR_ideal2 = Kp + tf([Kr,0],[1,0,wo^2])
Kr=100;
PR_ideal3 = Kp + tf([Kr,0],[1,0,wo^2])
figure(4)
bode(PR_ideal1,PR_ideal2,PR_ideal3)
grid on
title('Bode Diagram of ideal PR: Kp = 1. Kr = 1,10,100')

上面理想PR的波特图，可以看到就算调整PR的参数，波形也没什么大的变化。在实际使用中，可能进行实时调参的。图像变化这么小，跟踪效果也不会好。接下来看看实际使用的PR控制器的波特图。下图是当Kp分别取为1、10、100，Kr=1时实际的PR控制器的波特图（蓝 {MOD}是Kp=1，绿 {MOD}是Kp=10，红 {MOD}是Kp=100）。

附实现代码

Kr=1;
Kp=1;
PR1=Kp+tf([2*Kr*wc,0],[1,2*wc,wo^2])
Kp=10;
PR2=Kp+tf([2*Kr*wc,0],[1,2*wc,wo^2])
Kp=100;
PR3=Kp+tf([2*Kr*wc,0],[1,2*wc,wo^2])
bode(PR1,PR2,PR3)
grid on
title('Bode Diagram of actual PR: Kp = 1,10,100. Kr = 1')

下图是当Kp=1，Kr分别取为1、10、100时实际的PR控制器的波特图（蓝 {MOD}是Kr=1，绿 {MOD}是Kr=10，红 {MOD}是Kr=100）。

附实现代码

Kp=1;
Kr=1;
PR1=Kp+tf([2*Kr*wc,0],[1,2*wc,wo^2])
Kr=10;
PR2=Kp+tf([2*Kr*wc,0],[1,2*wc,wo^2])
Kr=100;
PR3=Kp+tf([2*Kr*wc,0],[1,2*wc,wo^2])
bode(PR1,PR2,PR3)
grid on
title('Bode Diagram of actual PR: Kp = 1. Kr = 1,10,100')

PI和PR的Kp作用类似，都是增大开环增益，增加控制精度。 Ki和Kr作用类似：降低系统稳态误差。

2、离散化预备知识

目的是对PR控制器的传递函数进行离散化。使其可以在数字控制器上编程实现。在这过程之前，要复习相关知识。同时便于检查离散化过程有无错误。

2.1 离散化表达式

传递函数离散化后，函数中消掉了拉普拉斯算子“s”，同时出现了“z”。有一个公式需要认识。 $frac{Yleft ( z ight )}{Uleft ( z ight )}=frac{a_0+a_1z^{-1}+a_2z^{-2}+...+a_nz^{-n}}{b_0+b_1z^{-1}+b_2z^{-2}+...+b_nz^{-n}}$ 以上公式，转化为单片机或DSP可以执行的命令为： b_0yleft ( k
ight )+b_1yleft ( k-1
ight )+b_2yleft ( k-2
ight )+...+b_nyleft ( k-n
ight )=a_0uleft ( k
ight )+a_1uleft ( k-1
ight )+a_2uleft ( k-2
ight )+...+a_nuleft ( k-n
ight )

b_0yleft ( k
ight )+b_1yleft ( k-1
ight )+b_2yleft ( k-2
ight )+...+b_nyleft ( k-n
ight )=a_0uleft ( k
ight )+a_1uleft ( k-1
ight )+a_2uleft ( k-2
ight )+...+a_nuleft ( k-n
ight )

2.2 离散化方法

离散化方法一览表[来自参考文献1] Zero-order hold $Xleft ( z ight )=left ( 1-z^{-1} ight )Zleft { L^{-1}left { frac{Xleft ( s ight )}{s} ight } ight }$ First-order hold $Xleft ( z ight )=frac{left ( z-1 ight )^2}{zT_s} Zleft { L^{-1}left { frac{Xleft ( s ight )}{s^2} ight } ight }$ Forward Euler $s=frac{z-1}{T_s}$ Backward Euler $s=frac{z-1}{zT_s}$ Trapezoid(Tustin) $s=frac{2}{T_s}frac{z-1}{z+1}$ Tustin with pre-warping $s=frac{omega _0}{tanleft ( frac{omega _0T_s}{2} ight )}frac{z-1}{z+1}$ Zero-pole matching $z=e^{sT_s}$ Impulse invariant $Xleft ( z ight )=Zleft { L^{-1}left { Xleft ( s ight ) ight } ight }$ 看起来比较简单的方法是Forward Euler、Backward Euler、Trapezoid(Tustin)这三种了。直接把公式代入，用z消掉s就好了。

2.3 离散化练习题

用Trapezoid(Tustin)方法离散化PID控制器。 $frac{Yleft ( s ight )}{Uleft ( s ight )}=K_p+frac{K_i}{s}+K_ds$ 把 $s=frac{2}{T_s}frac{z-1}{z+1}$ 代入上式，得到 $frac{Yleft ( s ight )}{Uleft ( s ight )}=K_p+frac{K_i}{frac{2}{T_s}frac{z-1}{z+1}}+K_dfrac{2}{T_s}frac{z-1}{z+1}$ 化简过程略，得到： $frac{Yleft ( z ight )}{Uleft ( z ight )}= frac{frac{left ( 2T_sK_p+T_s^2K_i+4K_d ight )}{2T_s}+frac{left ( 2T_s^2K_i-8K_d ight )}{2T_s}z^{-1}+frac{left ( -2T_sK_p+T_s^2K_i+4K_d ight )}{2T_s}z^{-2}}{1-z^{-2}}$ 代入Kp=1；Ki=2；Kd=3；Ts=1/1000；可得到 $frac{Yleft ( z ight )}{Uleft ( z ight )}= frac{6001-12000z^{-1}+5999z^{-2}}{1-z^{-2}}$ 在Matlab中验证结果：

 Kp=1;Ki=2;Kd=3;Ts=1e-3;
 PID=tf([Kd,Kp,Ki],[1,0])
 c2d(PID,1e-3,'tustin')

可得到： Transfer function:
6001 z^2 - 1.2e004 z + 5999
---------------------------
z^2 - 1

Sampling time: 0.001 和计算结果一致。同时Matlab的c2d()函数总共支持五种离散方法。


    SYSD = C2D(SYSC,TS,METHOD) computes a discrete-time model SYSD with 
    sampling time TS that approximates the continuous-time model SYSC.
    The string METHOD selects the discretization method among the following:
       'zoh'       Zero-order hold on the inputs
       'foh'       Linear interpolation of inputs
       'impulse'   Impulse-invariant discretization
       'tustin'    Bilinear (Tustin) approximation.
       'matched'   Matched pole-zero method (for SISO systems only).
    The default is 'zoh' when METHOD is omitted.

3. 使用Matlab离散PR控制器

Kp=1;
Kr=10;
wc=2*pi*5;
wo=2*pi*50;
PRs=Kp+tf([2*Kr*wc,0],[1,2*wc,wo^2])
PRz = c2d(PRs,1e-3,'tustin')

命令行输出： Transfer function:
1.297 z^2 - 1.847 z + 0.643
---------------------------
z^2 - 1.847 z + 0.9405

Sampling time: 0.001 可得到，离散化后，数字实现的C语言为： y_k - 1.847*y_k1 + 0.9405*y_k2 = 1.297*u_k - 1.847*u_k1 +0.643*u_k2; 即 y_k = 1.297*u_k - 1.847*u_k1 +0.643*u_k2 + 1.847*y_k1 - 0.9405*y_k2 ;

4、逆变器仿真模型中使用PR闭环控制器

Matlab/Simulink搭建了模型：

电气主回路中参数：滤波电感Lf=47uH，滤波电容Cf=1uF，负载Lf1=30欧姆。控制回路：

PR控制器实现框图：

经过参数优化后，Kp=1000，Kr=100；wc=2*pi*5；wo=2*pi*50；

上图中，error = Vref - Vout/311。Vref为频率50Hz、幅值为1的正弦波。Vout是逆变器输出。可以看到闭环系统中误差可降到1mV *311=0.331V之内（1mV为error波形的幅值，311为电压标幺化基准值）。
参考资料1：Effects of Discretization Methods on the Performance of Resonant Controllers, Alcjandro G. Ycpcs, IEEE transactions on Power Electronics 参考资料2：PID控制器的数字实现及C语法讲解参考资料3：比例谐振控制的一种实现（含代码）参考资料4：采用比例谐振控制器的逆变器_叶礼清