上几篇文章写了DFT/FFT、插值、压缩、滤波器等数字信号处理中的算法,今天写一下STFT算法(其实我刚开始是想搞小波变换wavelet的,搞了个大概就转成STFT了)的介绍。另外,我还模仿安捷伦示波器写了CF值为3.1/4.8/6.0/7.0的高斯随机数生成算法(极限推导理论CF=Vpp/Vrms值为6,我的算法还存在缺陷),还有一下乱七八糟的算法就不拿出来丢人了 。这些算法都是很久以前仓促完成的,有好多待优化的地方,代码风格可能也比较乱,努力改正!
。这些算法都是很久以前仓促完成的,有好多待优化的地方,代码风格可能也比较乱,努力改正! 注:我比较喜欢使用matlab(也喜欢自己修改matlab的源码做测试,所以重装了好几次了,囧。。。),有部分参考matlab的算法进行(或者直接翻译为OC),算法的运行结果经常会跟matlab运算结果进行比较,算法只做学习用,转载请注明。
另外着手写这些算法时,我还是obj-c小白,可能会有代码、算法不足或者理解偏差的地方,路过的高人请不吝赐教。
注:我比较喜欢使用matlab(也喜欢自己修改matlab的源码做测试,所以重装了好几次了,囧。。。),有部分参考matlab的算法进行(或者直接翻译为OC),算法的运行结果经常会跟matlab运算结果进行比较,算法只做学习用,转载请注明。
另外着手写这些算法时,我还是obj-c小白,可能会有代码、算法不足或者理解偏差的地方,路过的高人请不吝赐教。
STFT开始! ============================================================ 一、先说说STFT的理论 1.概念和特点 STFT(short-time Fourier transform,短时傅里叶变换)是和傅里叶变换相关的一种数学变换,用以确定时变信号其局部区域正弦波的频率与相位。
用途:与小波变换相似,经STFT处理后的信号具有时域和频域的局部化特性(见下图),可以借助其分析信号的视频特性。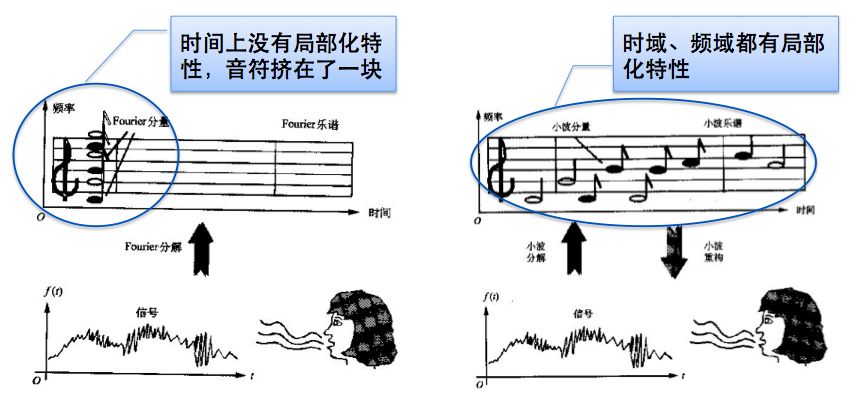
局限:STFT的使用范围受其变换性质的局限。STFT是一种基于窗函数的变换,一般来说,短窗能够提供较好的时域解析度,长窗能够提供较好的频域解析度。这导致其实在研究过程中,还是只能侧重一种研究角度,或称一种侧重的分辨率。所以这并不是多分辨率分析。这也是为什么之后又提出了小波变换的原因之一。 2.原理简介 以下介绍的与其说是原理,不如说时如何理解短时傅里叶变换。 顾名思义,短时傅里叶变换就是将原来的傅里叶变换在时域截短为多段分别进行傅里叶变换,每一段记为时刻ti,对应FFT求出频域特性,就可以粗略估计出时刻ti时的频域特性(也就是同时指导了时域和频域的对应关系)。用于信号截短的工具叫做窗函数(宽度相当于时间长度),窗越小,时域特性越明显,但是此时由于点数过少导致FFT降低了精确度,导致频域特性不明显。因此说窗的选取(包括大小和类型)是一个博弈的过程,根据自己研究的角度,选取适合的窗即可,当然最好还是选小波变换。。。 另外,为了保证频域特性的基础上提高时域特性,经常选择前后窗函数重叠一部分,这样两个窗确定的时刻就比较接近就提高了时域分析能力。但不是重叠越多越好,重叠点数过多会大幅增加计算量,导致效率低下,因此前后窗重叠的点数也需要外加确定。 给张图方便理解,图中矩形表示窗,窗确定的时刻为窗的中间时刻: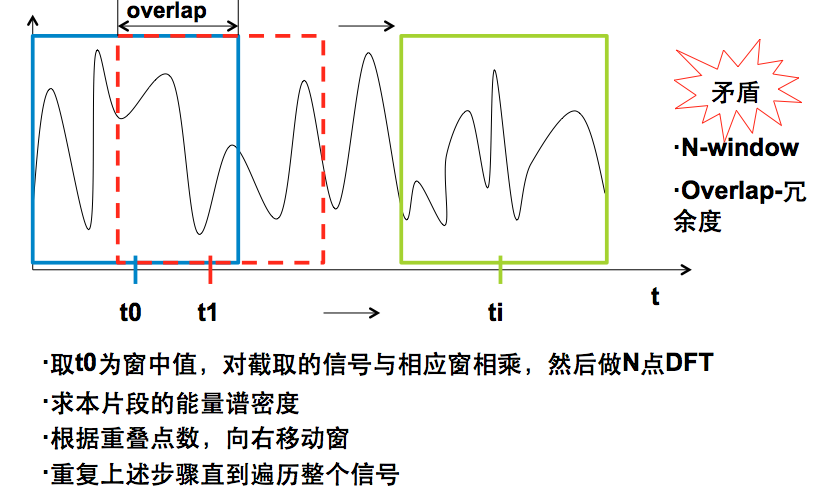 3.设计思路
对STFT已经有了初步的了解,那么就开始设计吧~设计思路如下:
(1)窗函数选择hamming窗,最大DFT点数不大于256;
(2)用户输入(传值):signal, window, overlap, N, fs等;
(3)根据窗的大小,将signal拆分,并与窗函数相乘;
(4)对每个signal片段进行N点FFT,并求出能量谱密度;
(5)调用绘图方法,把能量谱密度(功率谱密度)用不同的颜 {MOD}表示出来绘图。
说明:
(1)各种窗表达式
①海明窗(hamming):w(n)=0.54-0.46*cos(n/N);
②汉宁窗(hanning):w(n)=0.5*(1-cos(n/N));
③矩形窗(Rectangular):w(n)=1.0;
④三角窗(Triangle):w(n)=TRI(2n/N);
⑤布莱克曼窗(Blackman,三阶升余弦窗):w(n)=0.42-0.5*cos(n/N)+0.08*cos(2n/N);
⑥布莱克曼-哈里斯窗(BlackmanHarris):w(n)=0.35875-0.48829*cos(n/N)+0.14128*cos(2n/N)-0.01168*cos(3n/N);
(2)信号与窗的相乘
根据窗的长度截取响应长度的信号序列,然后二者对应的点逐点相乘,得到的数即为加窗截取后的值。之所以需要乘以窗函数,是因为如果直接截取信号,会使得截取的信号出现突变(波形上表现为直角),经过变换后会出现无限谐波影响截取后FFT的效果。
(3)绘图用到的颜 {MOD}
根据能量谱密度值的不同选择不同的颜 {MOD}表示,值从低到高对应颜 {MOD}从冷 {MOD}到暖 {MOD}变化。颜 {MOD} {MOD}谱如下图所示(冷→暖):
3.设计思路
对STFT已经有了初步的了解,那么就开始设计吧~设计思路如下:
(1)窗函数选择hamming窗,最大DFT点数不大于256;
(2)用户输入(传值):signal, window, overlap, N, fs等;
(3)根据窗的大小,将signal拆分,并与窗函数相乘;
(4)对每个signal片段进行N点FFT,并求出能量谱密度;
(5)调用绘图方法,把能量谱密度(功率谱密度)用不同的颜 {MOD}表示出来绘图。
说明:
(1)各种窗表达式
①海明窗(hamming):w(n)=0.54-0.46*cos(n/N);
②汉宁窗(hanning):w(n)=0.5*(1-cos(n/N));
③矩形窗(Rectangular):w(n)=1.0;
④三角窗(Triangle):w(n)=TRI(2n/N);
⑤布莱克曼窗(Blackman,三阶升余弦窗):w(n)=0.42-0.5*cos(n/N)+0.08*cos(2n/N);
⑥布莱克曼-哈里斯窗(BlackmanHarris):w(n)=0.35875-0.48829*cos(n/N)+0.14128*cos(2n/N)-0.01168*cos(3n/N);
(2)信号与窗的相乘
根据窗的长度截取响应长度的信号序列,然后二者对应的点逐点相乘,得到的数即为加窗截取后的值。之所以需要乘以窗函数,是因为如果直接截取信号,会使得截取的信号出现突变(波形上表现为直角),经过变换后会出现无限谐波影响截取后FFT的效果。
(3)绘图用到的颜 {MOD}
根据能量谱密度值的不同选择不同的颜 {MOD}表示,值从低到高对应颜 {MOD}从冷 {MOD}到暖 {MOD}变化。颜 {MOD} {MOD}谱如下图所示(冷→暖):

①在matlab中colorbar可以调出颜 {MOD}条图,如colorbar,colorbar('North')等,North表示在top出现颜 {MOD}条,另外还有East, West, South等(详见matlab帮助help colorbar); ②在matlab中colormap可以调出颜 {MOD}条图对应的RGB值数组; ③复制一下RGB对应的数组如下: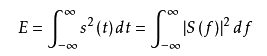
②在MATLAB中计算过程是 首先对截短的信号分别进行FFT并求模的平方(实部平方+虚部平方),然后除以窗函数的平方和得到Sxx。根据Sxx计算第一项分量(直流分量10lg10(|Sxx/fs|))、中间项(交流分量10lg10(|2*Sxx/fs|))和最后一项(fft计算点数为奇数与中间项一致,否则与第一项一致)。 附带matlab程序代码查看方法:在command窗口输入edit spectrogram,回车即可。
二、程序的实现
上面的介绍已经说明了设计思路,这里就不画流程图,直接上代码了 1.spectrogram方法 本部分的代码完全模仿matlab做的,所以如果有什么不明白的可以去查看matlab源码。另外,本部分的代码没有拆分,而是把所有的功能都用一个方法实现,自觉地给自己一个差评。。。 注:写本部分代码的时候我对objc还是小白,所以基本用的都是c语言的格式。。。
在上面的代码中Drawing类是自定义的一个绘图类,完成的功能是将数据点显示在模拟器上。绘图的流程时先给定绘图区域的四个顶点坐标和分区块数,然后指定绘图区域序号进行指定区域绘图。 绘图思想是:将给定的数据点确定范围后,一一对应冷暖 {MOD}条中的颜 {MOD},然后绘制每一个颜 {MOD}点即可。给出绘制颜 {MOD}点方法如下:
三、运行测试 1.先看看STFT观察跳频 给定波形由三个频率的信号叠加而成: signal1(freq=100Hz,Amp=2V) signal2(freq=150Hz,Amp=2V) signal3(freq=300Hz,Amp=1.5V) ①利用MATLAB测试 代码: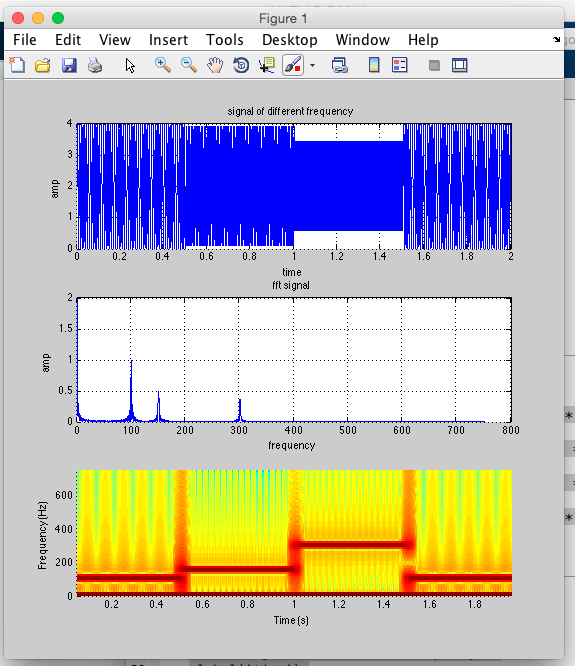
②利用iOS程序测试,结果如下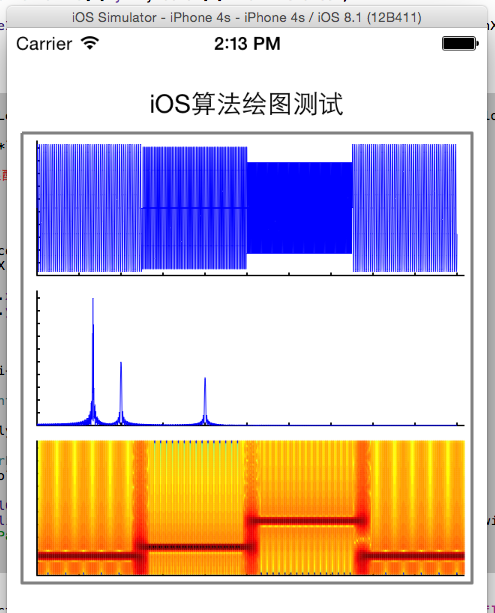
③结果简单总结,从上面两幅图可以看出, A.matlab运行的结果含有直流分量绘图(iOS去掉了)。 B.另外颜 {MOD}有偏差,原因可能是功率谱密度与冷暖 {MOD}条对应的方式不同(我没深究。。。)。 2.再看看STFT观察对语音的分析 注:这里的语音时matlab自带的一种小鸟的叫声,可以在matlab的command窗口键入①load chirp;②sound(y)或者sound(y,Fs)听一下。
①看看matlab程序及结果 代码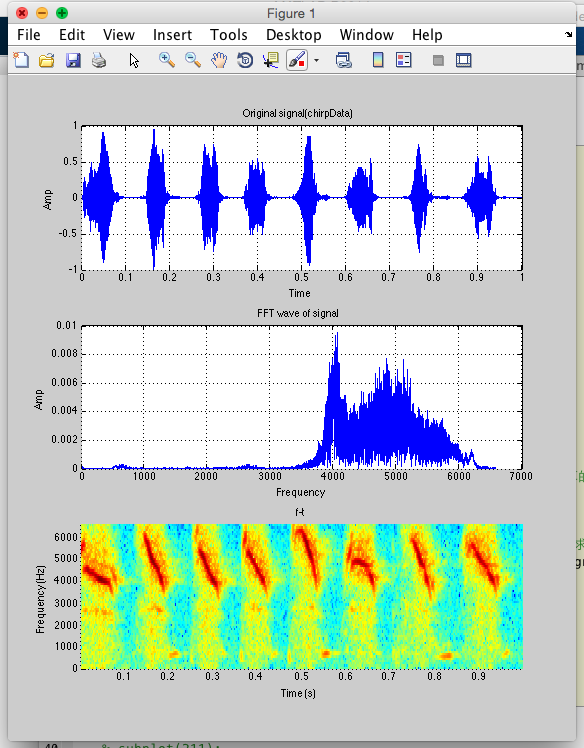
②看看ios的测试结果
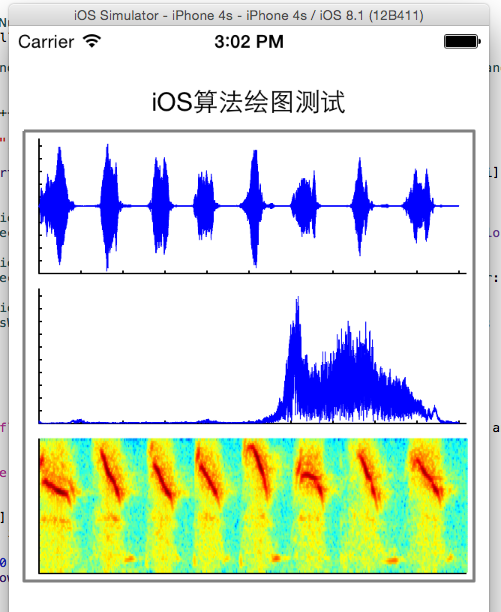
③结论 从图中看差不多完全一样,还有些小激动呢~
3.比一比Matlab和iOS的效率如何 说是比一比效率,其实就是看谁跑得快,看谁用时多。效率与当前的运行环境等各种因素有关,所以这里只做简单的测试。。。下标是经过多次测试后去多个靠谱的数平均得到的。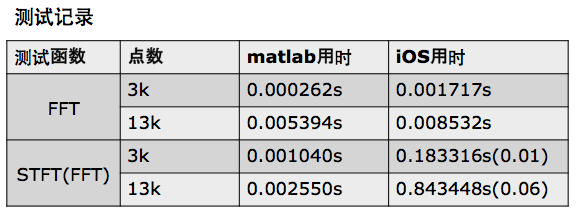
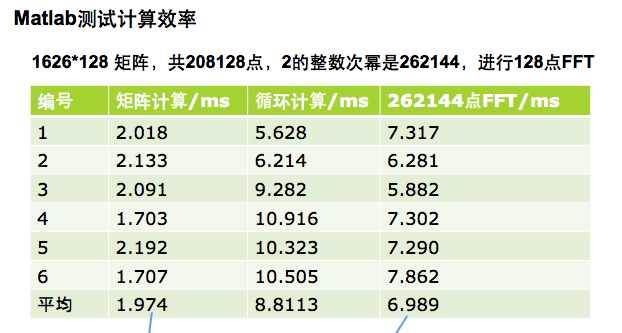
看看人家运行的效率,好奇心四起有木有?!!!!我将继续。。。
另外,附代码用时测试的方法
============================================ OK,STFT也结束了~~
 。这些算法都是很久以前仓促完成的,有好多待优化的地方,代码风格可能也比较乱,努力改正!
。这些算法都是很久以前仓促完成的,有好多待优化的地方,代码风格可能也比较乱,努力改正! 注:我比较喜欢使用matlab(也喜欢自己修改matlab的源码做测试,所以重装了好几次了,囧。。。),有部分参考matlab的算法进行(或者直接翻译为OC),算法的运行结果经常会跟matlab运算结果进行比较,算法只做学习用,转载请注明。
另外着手写这些算法时,我还是obj-c小白,可能会有代码、算法不足或者理解偏差的地方,路过的高人请不吝赐教。
注:我比较喜欢使用matlab(也喜欢自己修改matlab的源码做测试,所以重装了好几次了,囧。。。),有部分参考matlab的算法进行(或者直接翻译为OC),算法的运行结果经常会跟matlab运算结果进行比较,算法只做学习用,转载请注明。
另外着手写这些算法时,我还是obj-c小白,可能会有代码、算法不足或者理解偏差的地方,路过的高人请不吝赐教。
STFT开始! ============================================================ 一、先说说STFT的理论 1.概念和特点 STFT(short-time Fourier transform,短时傅里叶变换)是和傅里叶变换相关的一种数学变换,用以确定时变信号其局部区域正弦波的频率与相位。
用途:与小波变换相似,经STFT处理后的信号具有时域和频域的局部化特性(见下图),可以借助其分析信号的视频特性。

局限:STFT的使用范围受其变换性质的局限。STFT是一种基于窗函数的变换,一般来说,短窗能够提供较好的时域解析度,长窗能够提供较好的频域解析度。这导致其实在研究过程中,还是只能侧重一种研究角度,或称一种侧重的分辨率。所以这并不是多分辨率分析。这也是为什么之后又提出了小波变换的原因之一。 2.原理简介 以下介绍的与其说是原理,不如说时如何理解短时傅里叶变换。 顾名思义,短时傅里叶变换就是将原来的傅里叶变换在时域截短为多段分别进行傅里叶变换,每一段记为时刻ti,对应FFT求出频域特性,就可以粗略估计出时刻ti时的频域特性(也就是同时指导了时域和频域的对应关系)。用于信号截短的工具叫做窗函数(宽度相当于时间长度),窗越小,时域特性越明显,但是此时由于点数过少导致FFT降低了精确度,导致频域特性不明显。因此说窗的选取(包括大小和类型)是一个博弈的过程,根据自己研究的角度,选取适合的窗即可,当然最好还是选小波变换。。。 另外,为了保证频域特性的基础上提高时域特性,经常选择前后窗函数重叠一部分,这样两个窗确定的时刻就比较接近就提高了时域分析能力。但不是重叠越多越好,重叠点数过多会大幅增加计算量,导致效率低下,因此前后窗重叠的点数也需要外加确定。 给张图方便理解,图中矩形表示窗,窗确定的时刻为窗的中间时刻:
 3.设计思路
对STFT已经有了初步的了解,那么就开始设计吧~设计思路如下:
(1)窗函数选择hamming窗,最大DFT点数不大于256;
(2)用户输入(传值):signal, window, overlap, N, fs等;
(3)根据窗的大小,将signal拆分,并与窗函数相乘;
(4)对每个signal片段进行N点FFT,并求出能量谱密度;
(5)调用绘图方法,把能量谱密度(功率谱密度)用不同的颜 {MOD}表示出来绘图。
说明:
(1)各种窗表达式
①海明窗(hamming):w(n)=0.54-0.46*cos(n/N);
②汉宁窗(hanning):w(n)=0.5*(1-cos(n/N));
③矩形窗(Rectangular):w(n)=1.0;
④三角窗(Triangle):w(n)=TRI(2n/N);
⑤布莱克曼窗(Blackman,三阶升余弦窗):w(n)=0.42-0.5*cos(n/N)+0.08*cos(2n/N);
⑥布莱克曼-哈里斯窗(BlackmanHarris):w(n)=0.35875-0.48829*cos(n/N)+0.14128*cos(2n/N)-0.01168*cos(3n/N);
(2)信号与窗的相乘
根据窗的长度截取响应长度的信号序列,然后二者对应的点逐点相乘,得到的数即为加窗截取后的值。之所以需要乘以窗函数,是因为如果直接截取信号,会使得截取的信号出现突变(波形上表现为直角),经过变换后会出现无限谐波影响截取后FFT的效果。
(3)绘图用到的颜 {MOD}
根据能量谱密度值的不同选择不同的颜 {MOD}表示,值从低到高对应颜 {MOD}从冷 {MOD}到暖 {MOD}变化。颜 {MOD} {MOD}谱如下图所示(冷→暖):
3.设计思路
对STFT已经有了初步的了解,那么就开始设计吧~设计思路如下:
(1)窗函数选择hamming窗,最大DFT点数不大于256;
(2)用户输入(传值):signal, window, overlap, N, fs等;
(3)根据窗的大小,将signal拆分,并与窗函数相乘;
(4)对每个signal片段进行N点FFT,并求出能量谱密度;
(5)调用绘图方法,把能量谱密度(功率谱密度)用不同的颜 {MOD}表示出来绘图。
说明:
(1)各种窗表达式
①海明窗(hamming):w(n)=0.54-0.46*cos(n/N);
②汉宁窗(hanning):w(n)=0.5*(1-cos(n/N));
③矩形窗(Rectangular):w(n)=1.0;
④三角窗(Triangle):w(n)=TRI(2n/N);
⑤布莱克曼窗(Blackman,三阶升余弦窗):w(n)=0.42-0.5*cos(n/N)+0.08*cos(2n/N);
⑥布莱克曼-哈里斯窗(BlackmanHarris):w(n)=0.35875-0.48829*cos(n/N)+0.14128*cos(2n/N)-0.01168*cos(3n/N);
(2)信号与窗的相乘
根据窗的长度截取响应长度的信号序列,然后二者对应的点逐点相乘,得到的数即为加窗截取后的值。之所以需要乘以窗函数,是因为如果直接截取信号,会使得截取的信号出现突变(波形上表现为直角),经过变换后会出现无限谐波影响截取后FFT的效果。
(3)绘图用到的颜 {MOD}
根据能量谱密度值的不同选择不同的颜 {MOD}表示,值从低到高对应颜 {MOD}从冷 {MOD}到暖 {MOD}变化。颜 {MOD} {MOD}谱如下图所示(冷→暖):

①在matlab中colorbar可以调出颜 {MOD}条图,如colorbar,colorbar('North')等,North表示在top出现颜 {MOD}条,另外还有East, West, South等(详见matlab帮助help colorbar); ②在matlab中colormap可以调出颜 {MOD}条图对应的RGB值数组; ③复制一下RGB对应的数组如下:
#pragma mark - 颜 {MOD}数组
//colorbar,colormap,定义冷暖 {MOD}条的RGB值
static float g_colorBarR[64] = {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.06250,0.1250,0.18750,0.2500,0.31250,0.3750,0.43750,0.500,0.56250,0.6250,0.68750,0.7500,0.81250,0.8750,0.93750,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0.93750,0.8750,0.81250,0.7500,0.68750,0.6250,0.56250,0.500};
static float g_colorBarG[64] = {0,0,0,0,0,0,0,0,0.0625,0.125,0.1875,0.250,0.3125,0.375,0.4375,0.500,0.5625,0.625,0.6875,0.750,0.8125,0.875,0.9375,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0.9375,0.875,0.8125,0.750,0.6875,0.625,0.5625,0.500,0.4375,0.375,0.3125,0.250,0.1875,0.125,0.0625,0,0,0,0,0,0,0,0,0};
static float g_colorBarB[64] = {0.5625,0.625,0.6875,0.750,0.8125,0.875,0.9375,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0.9375,0.875,0.8125,0.750,0.6875,0.625,0.5625,0.500,0.4375,0.375,0.3125,0.250,0.1875,0.125,0.0625,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};(4)能量谱密度(功率谱密度PSD)
①设一个能量信号 s(t)
的能量为E,则此信号的能量由下式决定:
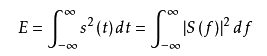
②在MATLAB中计算过程是 首先对截短的信号分别进行FFT并求模的平方(实部平方+虚部平方),然后除以窗函数的平方和得到Sxx。根据Sxx计算第一项分量(直流分量10lg10(|Sxx/fs|))、中间项(交流分量10lg10(|2*Sxx/fs|))和最后一项(fft计算点数为奇数与中间项一致,否则与第一项一致)。 附带matlab程序代码查看方法:在command窗口输入edit spectrogram,回车即可。
二、程序的实现
上面的介绍已经说明了设计思路,这里就不画流程图,直接上代码了 1.spectrogram方法 本部分的代码完全模仿matlab做的,所以如果有什么不明白的可以去查看matlab源码。另外,本部分的代码没有拆分,而是把所有的功能都用一个方法实现,自觉地给自己一个差评。。。 注:写本部分代码的时候我对objc还是小白,所以基本用的都是c语言的格式。。。
/**
* @brief 模仿MATLAB的spectrogram,实现STFT功能
* @param signalVector 原始信号序列
* @param N 信号的长度
* @param win 窗长度
* @param noverlap 窗重叠的点数
* @param nfft FFT/DFT的点数
* @param fs 抽样频率
* @param drawRect 绘图的区域rect
* @param context 绘图的上下文
* @return 是否计算成功的标志
*/
+ (Boolean)spectrogram:(float *)signalVector andLength:(int)N andWindowLength:(int)win andNoverlap:(int)noverlap andDFTCount:(int)nfft andFs:(int)fs andDrawRect:(CGRect)drawRect andContext:(CGContextRef)context
{
Boolean isSpecOK = false;
//hamming窗计算
float hammingWindow[win], windowPowValue = 0.0;
for(int i = 0; i < win; i++)
{
hammingWindow[i] = 0.54 - 0.46 * cosf(2*M_PI*i/(win-1));
windowPowValue += powf(hammingWindow[i], 2);
}
//计算短时傅里叶变换信号数组的行与列数,行数=时间点数,列数=窗长度
int row, column, halfNfft;
row = (N - noverlap)/(win - noverlap);
column = win;
halfNfft = nfft/2+1;
//计算t数组
float timeVector[row];
for(int i = 0; i < row; i++)
{
timeVector[i] = ((float)i) /((float)(fs*(win/2+1+(win-noverlap)*i)));
}
//将signal拆分
float signalXY[row][column];
for(int i = 0; i < row; i++)
{
for(int j = 0; j < column; j++)
{
signalXY[i][j] = signalVector[i*(win - noverlap) + j];
signalXY[i][j] *= hammingWindow[j];
}
}
//对拆分后的信号进行FFT
float fftReal[nfft], fftImg[nfft], Sxx[row][halfNfft], Pxx[row][halfNfft], logPxx[row][halfNfft], freq[nfft], freqStep, pxxMax, pxxMin;
freqStep = ((float)fs)/((float)nfft);
freq[0] = 0.0;
for(int i = 1; i < nfft; i++)
{
freq[i] = freqStep + freq[i-1];
}
//求Sxx
for(int i = 0; i < row; i++)
{
[FFT fft:signalXY[i] andOriginalLength:column andFFTCount:nfft andFFTReal:fftReal andFFTYImg:fftImg];
for(int j = 0; j < halfNfft; j++)
{
Sxx[i][j] = (fftReal[j]*fftReal[j] + fftImg[j]*fftImg[j])/windowPowValue;
}
}
//求Pxx
float fsFloat = (float)fs;
Pxx[0][0] = Sxx[0][0]/fsFloat;
logPxx[0][0] = 10*log10f(fabsf(Pxx[0][0]));
pxxMax = logPxx[0][0];
pxxMin = logPxx[0][0];
for(int i = 1; i < row; i++)
{
Pxx[i][0] = Sxx[i][0]/fsFloat;
logPxx[i][0] = 10*log10f(fabsf(Pxx[i][0]));
if(logPxx[i][0] > pxxMax)
pxxMax = logPxx[i][0];
if(logPxx[i][0] < pxxMin)
pxxMin = logPxx[i][0];
}
if(nfft%2)//奇数
{
for(int i = 0; i < row; i++)
{
for(int j = 1; j < halfNfft; j++)
{
Pxx[i][j] = Sxx[i][j]*2.0/((float)fs);
logPxx[i][j] = 10*log10f(fabsf(Pxx[i][j]));
if(logPxx[i][j] > pxxMax)
pxxMax = logPxx[i][j];
if(logPxx[i][j] < pxxMin)
pxxMin = logPxx[i][j];
}
}
}
else//偶数
{
for(int i = 0; i < row; i++)
{
Pxx[i][halfNfft-1] = Sxx[i][halfNfft-1]/((float)fs);
logPxx[i][halfNfft-1] = 10*log10f(fabsf(Pxx[i][halfNfft-1]));
if(logPxx[i][halfNfft-1] > pxxMax)
pxxMax = logPxx[i][halfNfft-1];
if(logPxx[i][halfNfft-1] < pxxMin)
pxxMin = logPxx[i][halfNfft-1];
}
for(int i = 0; i < row; i++)
{
for(int j = 1; j < halfNfft-1; j++)
{
Pxx[i][j] = Sxx[i][j]*2.0/((float)fs);
logPxx[i][j] = 10*log10f(fabsf(Pxx[i][j]));
if(logPxx[i][j] > pxxMax)
pxxMax = logPxx[i][j];
if(logPxx[i][j] < pxxMin)
pxxMin = logPxx[i][j];
}
}
}
//绘图
NSMutableArray *dataArray = [[NSMutableArray alloc] init];
for(int i = 0; i < row; i++)
{
for(int j = 0; j < halfNfft; j++)
{
NSNumber *numberMax = [NSNumber numberWithFloat:logPxx[i][j]];
[dataArray addObject:numberMax];
}
}
NSArray *colorArray = [[NSArray alloc] initWithArray:[Drawing getColorArrayByValue:dataArray andLengthX:row andLengthY:halfNfft andMax:pxxMax andMin:pxxMin]];
CGPoint p1, p2;
p1 = drawRect.origin;
p2.x = p1.x + drawRect.size.width;
p2.y = p1.y + drawRect.size.height;
Drawing *drawing = [[Drawing alloc] init];
[drawing setEnableDrawFieldLeftTopPoint:p1 andRightBottomPoint:p2 andContext:context];
int nfftAll = [FFT nextNumOfPow2:N];
float fftRealTest[nfftAll], fftImgTest[nfftAll];
[FFT fft:signalVector andOriginalLength:N andFFTCount:nfftAll andFFTReal:fftRealTest andFFTYImg:fftImgTest];
float t[N];
for(int i = 0; i < N; i++)
{
printf("%f + %fi ", fftRealTest[i], fftImgTest[i]);
t[i] = i;
fftRealTest[i] = sqrtf((fftImgTest[i]*fftImgTest[i] + fftRealTest[i]*fftRealTest[i]))/nfftAll;
}
[drawing selectSubDrawFieldWithRow:3 andColumn:1 andNumber:1];
[drawing drawLineWithXVector:t andYVector:signalVector andLength:N andLineColor:[UIColor blueColor]];
[drawing selectSubDrawFieldWithRow:3 andColumn:1 andNumber:2];
[drawing drawLineWithXVector:t andYVector:fftRealTest andLength:nfftAll/2 andLineColor:[UIColor blueColor]];
[drawing selectSubDrawFieldWithRow:3 andColumn:1 andNumber:3];
[drawing drawColorPointsWithLengthX:row andLengthY:halfNfft andColorArray:colorArray];
return isSpecOK;
}2.绘图方法在上面的代码中Drawing类是自定义的一个绘图类,完成的功能是将数据点显示在模拟器上。绘图的流程时先给定绘图区域的四个顶点坐标和分区块数,然后指定绘图区域序号进行指定区域绘图。 绘图思想是:将给定的数据点确定范围后,一一对应冷暖 {MOD}条中的颜 {MOD},然后绘制每一个颜 {MOD}点即可。给出绘制颜 {MOD}点方法如下:
//一次性画多个颜 {MOD}点
- (void)drawColorPointsWithLengthX:(int)lx andLengthY:(int)ly andColorArray:(NSArray *)colors
{
if([colors count] != lx*ly)
{
NSLog(@"错误,长度不匹配!");
exit(1);
}
float point_x, point_y;
UIColor *pointColor = [colors objectAtIndex:0];
float divX, divY, widthX, widthY;
divX = (cornerPoints[1].x - cornerPoints[0].x - 0.6)/((float)lx);
divY = (cornerPoints[2].y - cornerPoints[0].y - 1.0)/((float)ly);
widthX = ceilf(divX);
widthY = ceilf(divY);
for(int i = 0; i < lx; i++)
{
point_x = cornerPoints[0].x + 0.6 + divX*i;
int countx = i*ly;
for(int j = 0; j < ly; j++)
{
point_y = cornerPoints[2].y - 2.5 - divY*j;
pointColor = [colors objectAtIndex:countx+j];
CGContextSetFillColorWithColor(drawContext, [pointColor CGColor]);
CGContextFillEllipseInRect(drawContext, CGRectMake(point_x, point_y, widthX, widthY));
//CGContextFillPath(drawContext); //填充颜 {MOD}
}
}
}好啦,该努力的都努力完了,看看效果吧~~~
三、运行测试 1.先看看STFT观察跳频 给定波形由三个频率的信号叠加而成: signal1(freq=100Hz,Amp=2V) signal2(freq=150Hz,Amp=2V) signal3(freq=300Hz,Amp=1.5V) ①利用MATLAB测试 代码:
%% 变频信号的fft观察
close all
clear,clc
%% 定义一个变频信号的参数
PIx2 = 2 * pi;
Fs = 1500;
T = 1/Fs;
LengthOfSignal = 3000;
NFFT = 2^nextpow2(LengthOfSignal); %要计算的点数
% NFFT = 128;
t = (0:LengthOfSignal-1)*T;
amp1 = 2;
amp2 = 2;
amp3 = 1.5;
offset = 2;
freq1 = 100;
freq2 = 150;
freq3 = 300;
signal = zeros(1,length(t));
%% 定义信号
for temp = 1:LengthOfSignal
if(temp <= LengthOfSignal/4)
signal(temp) =offset + amp1 * sin(PIx2 * freq1 * t(temp));
elseif(temp <= LengthOfSignal/2)
signal(temp) =offset -1*amp2 * sin(PIx2 * freq2 * t(temp));
elseif(temp <= 3*LengthOfSignal/4)
signal(temp) =offset -1*amp3 * sin(PIx2 * freq3 * t(temp));
else
signal(temp) =offset + amp1 * sin(PIx2 * freq1 * t(temp));
end
end
%% 绘制图形
subplot(311);
plot(t, signal);
grid on
title('signal of different frequency');
xlabel('time');
ylabel('amp');
%% fft运算
fMax = NFFT/2 + 1;
signalFFT = abs(fft(signal,NFFT));
% signalFFTShow = 2 * abs(fft(signal(1:fMax),NFFT)/LengthOfSignal);
signalFFTShow = 2 * signalFFT / LengthOfSignal;
signalFFTShow(1) = signalFFTShow(1)/2;
f = Fs/2*linspace(0,1,fMax);
subplot(312);
plot(f,signalFFTShow(1:fMax));
grid on
title('fft signal');
xlabel('frequency');
ylabel('amp');
%% surf测试三维图(不合理x(j),y(i),z(i,j)对应)
subplot(313)
spectrogram(signal,128,120,128,1.5e3,'yaxis'); %时频域图
运行结果

②利用iOS程序测试,结果如下

③结果简单总结,从上面两幅图可以看出, A.matlab运行的结果含有直流分量绘图(iOS去掉了)。 B.另外颜 {MOD}有偏差,原因可能是功率谱密度与冷暖 {MOD}条对应的方式不同(我没深究。。。)。 2.再看看STFT观察对语音的分析 注:这里的语音时matlab自带的一种小鸟的叫声,可以在matlab的command窗口键入①load chirp;②sound(y)或者sound(y,Fs)听一下。
①看看matlab程序及结果 代码
%% spectrogram分析chirp声音
close all
clear,clc
%% 基本运算部分
load chirpData %载入数据(声音)
signalOfChirp = chirpData';
signalOfChirp_5 = signalOfChirp/5;
lengthOfSignal = length(signalOfChirp);
Fs = lengthOfSignal; %采样频率
T = 1/Fs;
t = (0:lengthOfSignal-1)*T;
% 绘原始波形图
figure;
subplot(311);
plot(t, signalOfChirp);
grid on
title('Original signal(chirpData)');
xlabel('Time');
ylabel('Amp');
%% 计算信号的fft
NFFT = 2^nextpow2(lengthOfSignal); %求最接近2的幂的数作为FFT计算的点数
fMax = NFFT/2 + 1; %频域显示最大的频率
f = Fs/2*linspace(0,1,fMax); %确定f数组
signalFFT = abs(fft(signalOfChirp, NFFT)/lengthOfSignal); %求出fft并取模
signalFFT_5 = 5 * abs(fft(signalOfChirp_5, NFFT)/lengthOfSignal);
%绘制fft波形图
subplot(312);
plot(f,signalFFT(1:fMax));
grid on
title('FFT wave of signal');
xlabel('Frequency');
ylabel('Amp');
%% 绘制f-t图(STFT)
subplot(313);
spectrogram(signalOfChirp,128,120,128,Fs,'yaxis'); %时频域图
title('f-t');结果如下

②看看ios的测试结果

③结论 从图中看差不多完全一样,还有些小激动呢~
3.比一比Matlab和iOS的效率如何 说是比一比效率,其实就是看谁跑得快,看谁用时多。效率与当前的运行环境等各种因素有关,所以这里只做简单的测试。。。下标是经过多次测试后去多个靠谱的数平均得到的。


看看人家运行的效率,好奇心四起有木有?!!!!我将继续。。。

另外,附代码用时测试的方法
NSDate *start1 = [NSDate date];
// ...需要测试的代码
NSDate *end1 = [NSDate date];
NSLog(@"FFT time %f ", [end1 timeIntervalSinceDate:start1]);
============================================ OK,STFT也结束了~~