class="markdown_views prism-github-gist">
在一些应用中,序列的乘积也叫做调制,实现该运算的器件称为调制器。
实现相乘运算的器件称为乘法器。
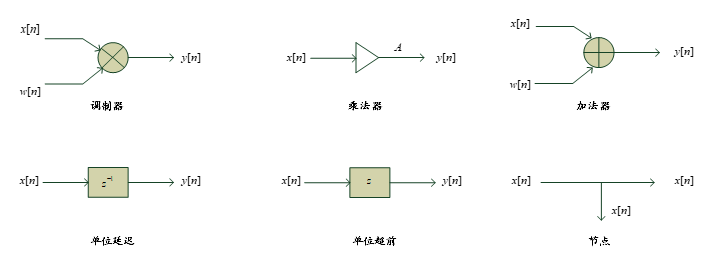
实现该运算的器件称为加法器。
若,则称之为延迟运算,若则称之为超前运算。 单位延迟为延迟一个单位,即
在变换中,延迟一个单位相当于乘以,所以在方框图用表示延迟一个单位 同理,单位超前一个单位可以写为
在变换中,超前一个单位相当于乘以,所以在方框图用表示超前一个单位
下面给出一些序列运算的例子,我将以图形的形式给出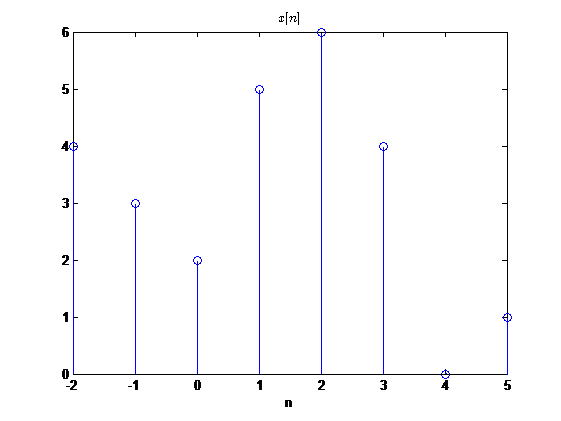
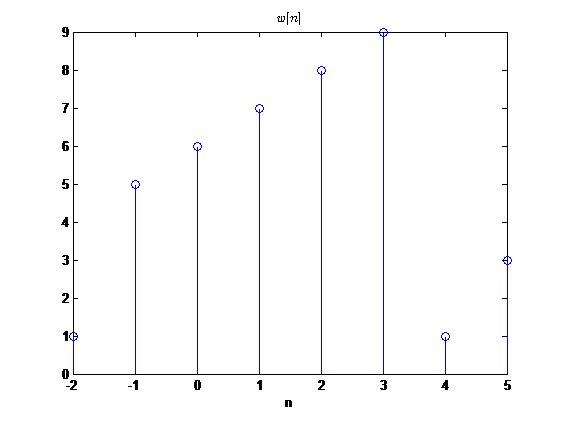 调制
调制
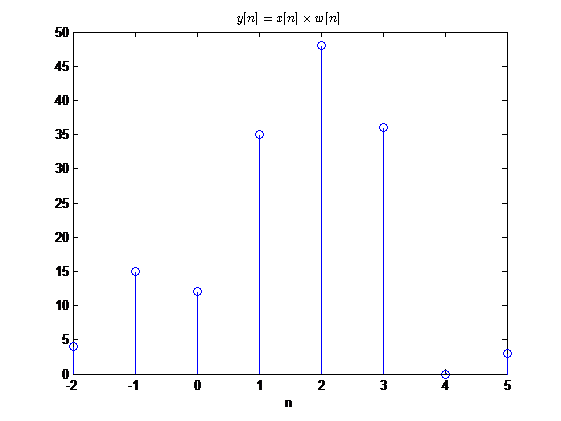
相加
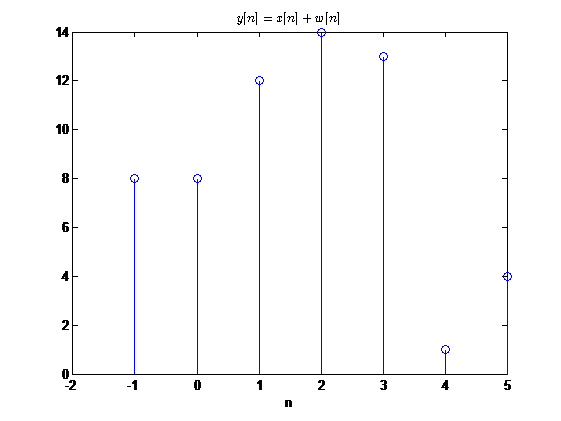
单位延迟

单位超前
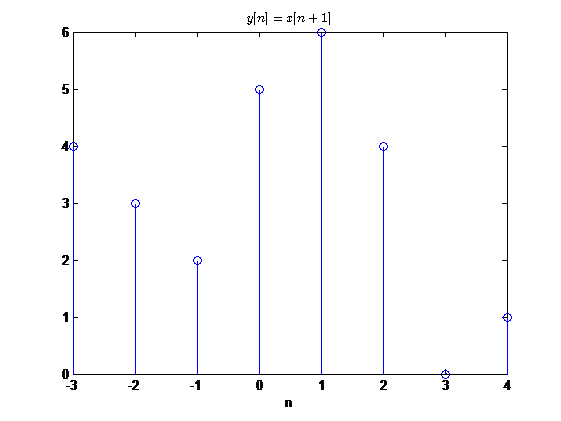
反褶
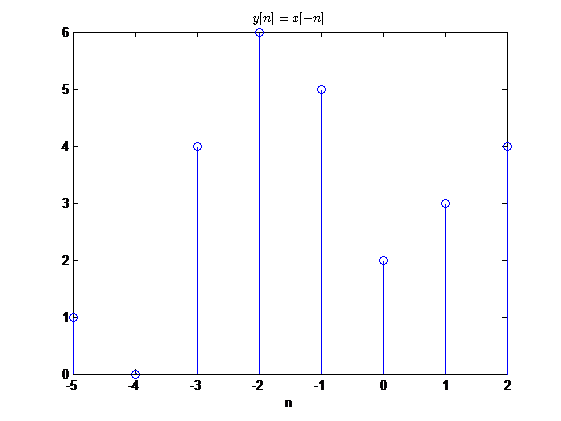
大多数的应用都是采用上述基本运算的组合。
至于为什么会有卷积和这种运算,在离散时间系统那里详细介绍过,卷积和可以说是信号与系统分析中最重要的运算之一。 观察卷积的表达式,发现卷积也是由基本运算组成的:首先对进行反褶得到,然后进行时移运算,由得到,然后进行调制运算,最后进行相加运算得到,所以一个卷积运算是由反褶,时移,调制,相加等基本运算组成的。 其实在实际的计算,计算过程就是由我上面所说的过程组成,从这里就可以看到,其实做卷积运算是比较麻烦的,在学习变换域时,有更好的办法进行卷积运算。 卷积和一般也写成
我们对上面的式子做一个变换,令,则:
所以卷积满足交换律。
观察表达式可以得到的下标和的下标加起来等于,所以想快速得到卷积后某一项的值可以快速的写出来,只要的下标加上的下标等于。 那么可以写为
这里假设和都是从开始的,并且和都能取到和。 当然对于不是从开始的也成立,假设是从开始的,是从开始的,那么
上述表达式成立前提是有和有。
序列的运算
基本运算
调制
两个序列样本值的乘积,指的是将两个序列的样本值逐点对应相乘,从而得到新的序列:在一些应用中,序列的乘积也叫做调制,实现该运算的器件称为调制器。
相乘
一个序列的每个样本值都乘以标量A以产生新的序列实现相乘运算的器件称为乘法器。

相加
把两个序列的样本值逐点的相加得到新的序列实现该运算的器件称为加法器。
时移
时移运算表现为若,则称之为延迟运算,若则称之为超前运算。 单位延迟为延迟一个单位,即
在变换中,延迟一个单位相当于乘以,所以在方框图用表示延迟一个单位 同理,单位超前一个单位可以写为
在变换中,超前一个单位相当于乘以,所以在方框图用表示超前一个单位
反褶
序列的反褶表现为下面给出一些序列运算的例子,我将以图形的形式给出

 调制
调制





卷积
和为两个序列,这两个序列通过卷积后产生新的序列是至于为什么会有卷积和这种运算,在离散时间系统那里详细介绍过,卷积和可以说是信号与系统分析中最重要的运算之一。 观察卷积的表达式,发现卷积也是由基本运算组成的:首先对进行反褶得到,然后进行时移运算,由得到,然后进行调制运算,最后进行相加运算得到,所以一个卷积运算是由反褶,时移,调制,相加等基本运算组成的。 其实在实际的计算,计算过程就是由我上面所说的过程组成,从这里就可以看到,其实做卷积运算是比较麻烦的,在学习变换域时,有更好的办法进行卷积运算。 卷积和一般也写成
我们对上面的式子做一个变换,令,则:
所以卷积满足交换律。
不做卷积得到某一项的值
如何快速展开得到卷积某一项的值,比如想得到的值。 假设的起点都是,那么可以快速写出观察表达式可以得到的下标和的下标加起来等于,所以想快速得到卷积后某一项的值可以快速的写出来,只要的下标加上的下标等于。 那么可以写为
这里假设和都是从开始的,并且和都能取到和。 当然对于不是从开始的也成立,假设是从开始的,是从开始的,那么
上述表达式成立前提是有和有。