DSP

窗函数在图像处理中的应用

2019-07-13 20:36发布生成海报

站内文章 / DSP

16272 0

窗函数在图像处理中的应用

上次我初略的讲了一下什么是窗函数，以及窗函数在DSP应用中的例子。之所以要引用窗函数，主要是为了防止突然的截断导致的频谱泄露。频谱的泄露在DIP的频域中也是非常常见的，我这里举三个例子来说明。如果还不了解窗函数的同学请看我写的这篇文章：https://blog.csdn.net/daduzimama/article/details/80050523

例1, 频谱混乱的三角函数图像

下图是一个负40度倾斜的单一频率的正弦函数图像，请注意图中的边界并不是均匀过渡到外界的，都是不连续的跳变。

clear all 
close all

%% FFT of 2D wave of trigonometry 
% Length of signal
L = 512;        
% Sampling frequency
FsLow = 300;
% Form sampling vectors
IndexLow = linspace(0,FsLow,L); 

% build 1D sinewave
SineLow = sin(IndexLow);

% translate 1D wave into 2D sinewave
SinewaveL = repmat(SineLow,[L,1]);

% Rotation angle of Sinewave 
Angle = -40;
Irot = imrotate(SinewaveL, Angle, 'loose', 'bilinear');

% figure out the image size of new Sinewave.
Start = floor(size(Irot,1)/4);
Stop = 3*Start;

% image crop
Icrop = Irot(Start:Stop,Start:Stop);

figure;
imshow(Icrop,[]);

下面我们来看看这幅图的频谱会是什么样呢？（下图）哇，怎么会这么乱呢。。。完全无法通过这个频谱图去理解一个具有单一频率的原始信号。

figure;
imshow(log(1 + abs(fftshift(fft2(Icrop)))),[]);

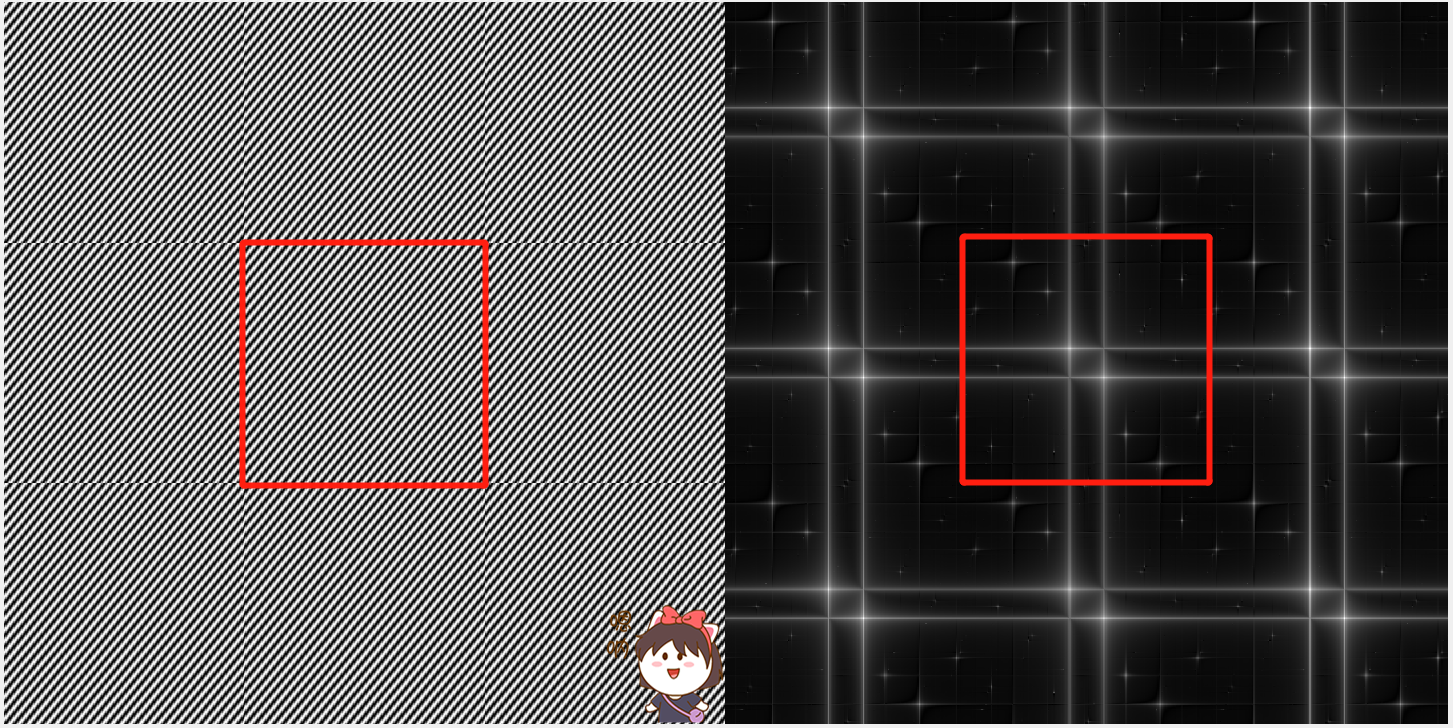
频谱混乱的原因 究其原因主要有两个：第一个重要的原因我在上一篇讲过了，就是一个域（不论是时域还是频域）的不连续导致了另一个域的振荡，拖尾，泄漏。所以下图中的频谱就会看起来非常的混乱。第二个原因就是DFT的周期性。当我们在使用MATLAB中的函数FFT或FFT2的时候，我们一定要意识到，我们所做的计算本质上离散傅里叶级数（为什么是级数而不是变换，我会再写一篇文章说明）Discrete Fourier transform（DFT）。要知道，DFT的计算隐含着默认的周期性，这一周期性不论是在时域还是在频域都是无穷的，都是无限循环的，从二维信号上讲，即沿着X方向循环复制，也在Y方向循环复制。下图中用红 {MOD}方框框出的只是其中的一个周期。

Iperiodic = repmat(Icrop,3,3);
figure;
imshowpair(Iperiodic,repmat((log(abs(fftshift(fft2(Icrop)))+1)), 3, 3),'montage');

请注意上图中左图中（空间域）余弦信号图和他相邻的图像在红 {MOD}边缘处的各种不连续（discontinuity）。这种不连续直接导致了右图中（频率域）及其混乱，复杂的频谱。所以，在处理任何图像时，千万不要忽视了图像的边缘。比如说，FFT之前的0填充，这也是一种会经常用到的避免频谱泄漏的有效方式。 汉宁窗 现在我们对原始图像进行加窗，这里我们选择的是汉宁窗（hanning window）。下图为汉宁窗的时间域函数图像及其频谱特征。窗函数的参数介绍以及窗函数的选择我自己涉及的不多，但是我推荐有兴趣的读者看看知乎上的这篇文章： https://zhuanlan.zhihu.com/p/24318554 总的来说，窗函数都比较光滑，就好像一个高斯滑动均值滤波器磨平了原始信号中边缘的不连续。

上图来自维基百科。

请注意上图中我用红框框出的几个重要参数，这是衡量窗函数的三个重要指标。

L = 64;
wvtool(hann(L))

对图像加窗 加窗后的频谱图远比加窗前的更集中，更清晰。

% Window function
Window = hanning(size(Icrop,1))*hanning(size(Icrop,2))';
SinewaveLwindowed = Icrop.*Window;

figure;
imshowpair(Window,SinewaveLwindowed,'montage');

figure;
imshowpair(log(1 + abs(fftshift(fft2(Icrop)))),log(1 + abs(fftshift(fft2(SinewaveLwindowed)))),'montage');

如果读者还是觉得加窗后的效果不太理想，可以更换窗函数并调整窗函数的参数，最终达到你想要的效果（让频谱的能量更加集中）。下面我改用著名的凯撒窗，看看效果如何。 凯撒窗

% try another window
Beta = 30;
N = 64;
w = kaiser(N,Beta);
wvtool(w)

Window = kaiser(size(Icrop,1),Beta)*kaiser(size(Icrop,1),Beta)';
SinewaveLwindowed = Icrop.*Window;

figure;
imshowpair(Window,SinewaveLwindowed,'montage');

figure;
imshowpair(log(1 + abs(fftshift(fft2(Icrop)))),log(1 + abs(fftshift(fft2(SinewaveLwindowed)))),'montage');

例2, 著名的Cameraman.tiff

刚才的那个例子中，空间域的不连续是非常明显，显而易见的（TIPS：一个域的不连续导致了另外一个域的频振荡和拖尾，不只是从空间域/时间域到频域是这样，VICE VERSA。）。下面我们在用图像处理中的经典图像，摄影师，来看另外一种情况。在这个例子中，边界上的跳变远没有上一个例子那么明显，但也会引起频谱的泄露，污染了（smear）真实的频谱信息，而这种情况最为常见，最容易被忽视。下图为cameraman的原图和频谱图，注意频谱图中我用箭头标出的一条白 {MOD}的中轴线，也是频谱的泄漏造成的。

%% Trial of Cameraman.tif
I = (im2double(imread('cameraman.tif')));
figure;
imshowpair(I,log(abs(fftshift(fft2(I)))+1),'montage');

产生这根白线的原因主要是，原始图像在DFT周期复制的时候，头顶的蓝天部分较亮，而脚下草坪部分较暗。由于图像横向边缘的灰度值突变（见下图），在频谱图中的Y方向产生了频谱的泄露。当然了，图像的纵向边缘也能看到一些灰度的不平滑过渡，势必也会引起图像频谱在X方向的改变，但在此例中并不明显。

% matrix repeat 
Iperiodic = repmat(I,3,3);
figure;
imshowpair(Iperiodic,repmat((log(abs(fftshift(fft2(I)))+1)), 3, 3),'montage');

下面看看加窗后的图像和加窗后频谱的改变。

频谱图中间的那条白线，没了！

% Window function
Window = hanning(size(I,1))*hanning(size(I,2))';
windowed = I.*Window;

figure;
imshowpair(I,windowed,'montage');

figure;
imshowpair(log(1 + abs(fftshift(fft2(I)))),log(1 + abs(fftshift(fft2(windowed)))),'montage');

例3, 上三角矩阵和下三角矩阵

理论上讲上三角矩阵和下三角矩阵的频谱都应该都只有一条斜线，不管是左斜还有右斜，但是往往大家看到的上/下三角矩阵的频谱图当中还有一个十字架。这都是因为没有加窗出现了DFT周期性的边界不连续。

注意图中的十字架，这是本不该出现在频谱图中的成分。

下图是加窗后的真实频谱，见下图。

%% Triangle
s = 512;
ItriangleUpper = triu(ones(s),0);

figure;
imshowpair(ItriangleUpper,log(abs(fftshift(fft2(ItriangleUpper)))+1),'montage');

Hanning = hanning(s)*hanning(s)';

ItriangleUpper = ItriangleUpper.*Hanning;
figure;
imshowpair(ItriangleUpper,log(abs(fftshift(fft2(ItriangleUpper)))+1),'montage');

总结这篇文章用三个简单的例子，粗略的解释了窗函数在DIP中的应用。实际图像处理的工作中，但凡是用到了频谱操作，很多时候正确的使用窗函数往往是大有裨益的，不要忘了他！谢谢收看！再见！ 《圣经》约翰福音14章21节 ------------ 有了我的命令又遵守的，这人就是爱我的。爱我的必蒙我父爱他，我也要爱他，并且要向他显现。

*配图与本文无关*